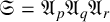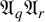1. Introduction
A group is an A-group if its nilpotent subgroups are abelian. For any class of groups
![]() ${\mathfrak {B}}$
, we denote the number of groups of order n up to isomorphism by
${\mathfrak {B}}$
, we denote the number of groups of order n up to isomorphism by
![]() $f_{\mathfrak {B}}(n)$
. Computing
$f_{\mathfrak {B}}(n)$
. Computing
![]() $f(n)$
becomes harder as n gets bigger. Thus, in the area of group enumerations, we attempt to approximate
$f(n)$
becomes harder as n gets bigger. Thus, in the area of group enumerations, we attempt to approximate
![]() $f(n)$
. When counting is restricted to the class of abelian groups, A-groups or groups in general, the asymptotic behaviour of
$f(n)$
. When counting is restricted to the class of abelian groups, A-groups or groups in general, the asymptotic behaviour of
![]() $f(n)$
varies significantly. Let
$f(n)$
varies significantly. Let
![]() $f_{A,sol}(n)$
be the number of isomorphism classes of soluble A-groups of order n. Dickenson [Reference Dickenson2] showed that
$f_{A,sol}(n)$
be the number of isomorphism classes of soluble A-groups of order n. Dickenson [Reference Dickenson2] showed that
![]() $f_{A,sol}(n) \leq n^{c \log {n}}$
for some constant c. McIver and Neumann [Reference McIver and Neumann7] showed that the number of nonisomorphic A-groups of order n is at most
$f_{A,sol}(n) \leq n^{c \log {n}}$
for some constant c. McIver and Neumann [Reference McIver and Neumann7] showed that the number of nonisomorphic A-groups of order n is at most
![]() $n^{{\lambda }+1}$
, where
$n^{{\lambda }+1}$
, where
![]() $\lambda $
is the number of prime divisors of n including multiplicities. In the same paper, they stated the following conjecture based on a result of Higman [Reference Higman4] and Sims [Reference Sims12] on p-group enumerations.
$\lambda $
is the number of prime divisors of n including multiplicities. In the same paper, they stated the following conjecture based on a result of Higman [Reference Higman4] and Sims [Reference Sims12] on p-group enumerations.
Conjecture 1.1. Let
![]() $f(n)$
be the number of (isomorphism classes of groups of) order n. Then
$f(n)$
be the number of (isomorphism classes of groups of) order n. Then
![]() $ f(n) \leq n^{({2}/{27} + \epsilon ){\lambda }^2}$
, where
$ f(n) \leq n^{({2}/{27} + \epsilon ){\lambda }^2}$
, where
![]() $\epsilon \to 0$
as
$\epsilon \to 0$
as
![]() $\lambda \to \infty $
.
$\lambda \to \infty $
.
In 1993, Pyber [Reference Pyber9] proved a powerful version of Conjecture 1.1: the number of groups of order n with specified Sylow subgroups is at most
![]() $n^{75 \mu + 16}$
, where
$n^{75 \mu + 16}$
, where
![]() $\mu $
is the largest integer such that
$\mu $
is the largest integer such that
![]() $p^{\mu }$
divides n for some prime p. From the results of Higman and Sims, and Pyber,
$p^{\mu }$
divides n for some prime p. From the results of Higman and Sims, and Pyber,
![]() $ f(n) \leq n^{{2}{\mu }^2/27 + O(\mu ^{5/3})}$
. In [Reference Venkataraman13], it was shown that
$ f(n) \leq n^{{2}{\mu }^2/27 + O(\mu ^{5/3})}$
. In [Reference Venkataraman13], it was shown that
![]() $f_{A,sol}(n) \leq n^{7\mu + 6}$
.
$f_{A,sol}(n) \leq n^{7\mu + 6}$
.
The variety
![]() ${\mathfrak {A}_u}{\mathfrak {A}_v}$
consists of all groups G with an abelian normal subgroup N of exponent dividing u such that
${\mathfrak {A}_u}{\mathfrak {A}_v}$
consists of all groups G with an abelian normal subgroup N of exponent dividing u such that
![]() $G/N$
is abelian of exponent dividing v. (For more on varieties, see [Reference Neumann8].) Let
$G/N$
is abelian of exponent dividing v. (For more on varieties, see [Reference Neumann8].) Let
![]() $p, q$
and r be distinct primes. In this paper, we find a bound for
$p, q$
and r be distinct primes. In this paper, we find a bound for
![]() $f_{\mathfrak {S}}(n)$
, where
$f_{\mathfrak {S}}(n)$
, where
![]() $\mathfrak {S}={\mathfrak {A}_p}{\mathfrak {A}_q}{\mathfrak {A}_r}$
and
$\mathfrak {S}={\mathfrak {A}_p}{\mathfrak {A}_q}{\mathfrak {A}_r}$
and
![]() $f_{\mathfrak {S}}(n)$
counts the groups in
$f_{\mathfrak {S}}(n)$
counts the groups in
![]() $\mathfrak {S}$
of order n up to isomorphism. The idea behind studying the variety
$\mathfrak {S}$
of order n up to isomorphism. The idea behind studying the variety
![]() $\mathfrak {S}$
is that enumerating within the varieties of A-groups might yield a better upper bound for the enumeration function for A-groups. The ‘best’ bounds for A-groups, or even soluble A-groups, still lack the correct leading term. It is believed that a correct leading term for the upper bound of A-groups would lead to the right error term for the enumeration of groups in general.
$\mathfrak {S}$
is that enumerating within the varieties of A-groups might yield a better upper bound for the enumeration function for A-groups. The ‘best’ bounds for A-groups, or even soluble A-groups, still lack the correct leading term. It is believed that a correct leading term for the upper bound of A-groups would lead to the right error term for the enumeration of groups in general.
A few smaller varieties of A-groups have already been studied in [Reference Blackburn, Neumann and Venkataraman1, Ch. 18]. The class of A-groups for which the ‘best’ bounds exist was obtained by enumerating in such small varieties of A-groups, but this did not narrow the difference between the upper and lower bounds for
![]() $f_{A,sol}(n)$
because these groups did not contribute a large enough collection of A-groups. Hence, a good lower bound could not be reached. To reduce the difference, we enumerate in the larger variety
$f_{A,sol}(n)$
because these groups did not contribute a large enough collection of A-groups. Hence, a good lower bound could not be reached. To reduce the difference, we enumerate in the larger variety
![]() $\mathfrak {S}$
of A-groups.
$\mathfrak {S}$
of A-groups.
Throughout the paper, p, q, r and t are distinct primes. We assume that s is a power of t. We take logarithms to the base
![]() $2$
, unless stated otherwise, and follow the convention that
$2$
, unless stated otherwise, and follow the convention that
![]() $0 \in \mathbb {N}$
. We use
$0 \in \mathbb {N}$
. We use
![]() $C_m$
to denote a cyclic group of order m for any positive integer m. Let
$C_m$
to denote a cyclic group of order m for any positive integer m. Let
![]() $O_{p'}{(G)}$
denote the largest normal
$O_{p'}{(G)}$
denote the largest normal
![]() $p'$
-subgroup of G. The techniques we use are similar to those in [Reference Blackburn, Neumann and Venkataraman1, Reference Pyber9, Reference Venkataraman13].
$p'$
-subgroup of G. The techniques we use are similar to those in [Reference Blackburn, Neumann and Venkataraman1, Reference Pyber9, Reference Venkataraman13].
The main result proved in this paper is the following theorem.
Theorem 1.2. Let
![]() $n=p^{\alpha }q^{\beta }r^{\gamma }$
, where
$n=p^{\alpha }q^{\beta }r^{\gamma }$
, where
![]() $\alpha , \beta , \gamma \in \mathbb { N}$
. Then,
$\alpha , \beta , \gamma \in \mathbb { N}$
. Then,
To prove Theorem 1.2, we prove a bound on the number of conjugacy classes of subgroups that are maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
and that are in the variety
$\mathrm{GL}(\alpha , s)$
and that are in the variety
![]() $\mathfrak {A}_q \mathfrak {A}_r$
or
$\mathfrak {A}_q \mathfrak {A}_r$
or
![]() $\mathfrak {A}_r$
. We also prove results about the order of primitive subgroups of
$\mathfrak {A}_r$
. We also prove results about the order of primitive subgroups of
![]() $S_n$
that are in the variety
$S_n$
that are in the variety
![]() $\mathfrak {A}_q \mathfrak {A}_r$
and show that they form a single conjugacy class. These results are stated below.
$\mathfrak {A}_q \mathfrak {A}_r$
and show that they form a single conjugacy class. These results are stated below.
Theorem 1.3. Let q and r be distinct primes. Let G be a primitive subgroup of
![]() $S_n$
that is in
$S_n$
that is in
![]() $\mathfrak {A}_q \mathfrak {A}_r$
and let
$\mathfrak {A}_q \mathfrak {A}_r$
and let
![]() $|G| = q^\beta r^\gamma $
, where
$|G| = q^\beta r^\gamma $
, where
![]() $\beta , \gamma \in \mathbb {N}$
. Let M be a minimal normal subgroup of G.
$\beta , \gamma \in \mathbb {N}$
. Let M be a minimal normal subgroup of G.
-
(i) If
 $\beta = 0$
, then
$\beta = 0$
, then
 $|M|$
is a power of r and
$|M|$
is a power of r and
 $|G| = n = r$
with
$|G| = n = r$
with
 $G \cong C_r$
.
$G \cong C_r$
. -
(ii) If
 $\beta \geq 1$
, then
$\beta \geq 1$
, then
 $|M| = q^{\beta } = n$
with
$|M| = q^{\beta } = n$
with
 $ \beta = {\mathrm{order}} \ q \bmod r$
. Further,
$ \beta = {\mathrm{order}} \ q \bmod r$
. Further,
 $G \cong M \rtimes C_r$
and
$G \cong M \rtimes C_r$
and
 $|G| = nr < n^{2}$
.
$|G| = nr < n^{2}$
. -
(iii) If
 $\gamma = 0$
, then
$\gamma = 0$
, then
 $|M|$
is a power of q and
$|M|$
is a power of q and
 $|G| = n = q$
with
$|G| = n = q$
with
 $G\cong C_q$
.
$G\cong C_q$
.
Theorem 1.4. The primitive subgroups of
![]() $S_n$
that are in
$S_n$
that are in
![]() $\mathfrak {A}_q \mathfrak {A}_r$
and of order
$\mathfrak {A}_q \mathfrak {A}_r$
and of order
![]() $q^{\beta }r^{\gamma }$
, where
$q^{\beta }r^{\gamma }$
, where
![]() $\beta , \gamma \in \mathbb { N}$
, form a single conjugacy class.
$\beta , \gamma \in \mathbb { N}$
, form a single conjugacy class.
Theorem 1.5. There exist constants b and c such that the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
where
![]() $t, q$
and r are distinct primes, s is a power of t, and
$t, q$
and r are distinct primes, s is a power of t, and
![]() $\alpha> 1$
.
$\alpha> 1$
.
Section 2 investigates primitive subgroups of
![]() $S_{n}$
that are in
$S_{n}$
that are in
![]() $\mathfrak {A}_r$
or
$\mathfrak {A}_r$
or
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. Sections 3 and 4 deal with subgroups of the general linear group. Theorem 1.2 is proved in Section 5.
$\mathfrak {A}_q\mathfrak {A}_r$
. Sections 3 and 4 deal with subgroups of the general linear group. Theorem 1.2 is proved in Section 5.
2. Primitive subgroups of
 $S_{n}$
that are in
$S_{n}$
that are in
 $\mathfrak {A}_r$
or
$\mathfrak {A}_r$
or
 $\mathfrak {A}_q\mathfrak {A}_r$
$\mathfrak {A}_q\mathfrak {A}_r$
In this section, we prove results that give us the structure of the primitive subgroups of
![]() $S_{n}$
that are in
$S_{n}$
that are in
![]() $\mathfrak {A}_r$
or
$\mathfrak {A}_r$
or
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. We also show that such subgroups form a single conjugacy class. Both Theorems 1.3 and 1.4 are proved in this section.
$\mathfrak {A}_q\mathfrak {A}_r$
. We also show that such subgroups form a single conjugacy class. Both Theorems 1.3 and 1.4 are proved in this section.
Theorem 1.3 provides the order of a primitive subgroup of
![]() $S_n$
that is in the variety
$S_n$
that is in the variety
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. By [Reference Venkataraman13, Proposition 2.1], if G is a soluble A-subgroup of
$\mathfrak {A}_q\mathfrak {A}_r$
. By [Reference Venkataraman13, Proposition 2.1], if G is a soluble A-subgroup of
![]() $S_n$
, then
$S_n$
, then
![]() $|G| \leq (6^{1/2})^{n-1}$
. Indeed, this bound is determined primarily by considering primitive soluble A-subgroups of
$|G| \leq (6^{1/2})^{n-1}$
. Indeed, this bound is determined primarily by considering primitive soluble A-subgroups of
![]() $S_n$
. This bound would clearly hold for any subgroup of
$S_n$
. This bound would clearly hold for any subgroup of
![]() $S_n$
that is in the variety
$S_n$
that is in the variety
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. However, we show that when the subgroup is primitive and in the variety
$\mathfrak {A}_q\mathfrak {A}_r$
. However, we show that when the subgroup is primitive and in the variety
![]() $\mathfrak {A}_q\mathfrak {A}_r$
, we can do better.
$\mathfrak {A}_q\mathfrak {A}_r$
, we can do better.
Lemma 2.1.
![]() $S_n$
has a primitive subgroup in
$S_n$
has a primitive subgroup in
![]() $\mathfrak {A}_r$
if and only if
$\mathfrak {A}_r$
if and only if
![]() $n=r$
. In this case, any primitive subgroup G that is in
$n=r$
. In this case, any primitive subgroup G that is in
![]() $\mathfrak {A}_r$
will be cyclic of order r. All primitive subgroups of
$\mathfrak {A}_r$
will be cyclic of order r. All primitive subgroups of
![]() $S_n$
that are in
$S_n$
that are in
![]() $\mathfrak {A}_r$
form a single conjugacy class.
$\mathfrak {A}_r$
form a single conjugacy class.
Proof. Let G be a primitive subgroup of
![]() $S_n$
that is in
$S_n$
that is in
![]() $\mathfrak {A}_r$
. Since G is soluble, M is an elementary abelian r-subgroup. By the O’Nan–Scott theorem [Reference Scott, Cooperstein and Mason10],
$\mathfrak {A}_r$
. Since G is soluble, M is an elementary abelian r-subgroup. By the O’Nan–Scott theorem [Reference Scott, Cooperstein and Mason10],
![]() $|M| = n = |G|$
, so
$|M| = n = |G|$
, so
![]() $G = M \cong C_{r}$
and
$G = M \cong C_{r}$
and
![]() $n=r$
. Conversely, any transitive subgroup G of
$n=r$
. Conversely, any transitive subgroup G of
![]() $S_{r}$
is primitive [Reference Wielandt15, Theorem 8.3]. Since n is prime, any subgroup of order n in
$S_{r}$
is primitive [Reference Wielandt15, Theorem 8.3]. Since n is prime, any subgroup of order n in
![]() $S_n$
will be generated by an n-cycle. Further, any two n-cycles are conjugate in
$S_n$
will be generated by an n-cycle. Further, any two n-cycles are conjugate in
![]() $S_n$
. Thus, the primitive subgroups of
$S_n$
. Thus, the primitive subgroups of
![]() $S_n$
that are also in
$S_n$
that are also in
![]() $\mathfrak {A}_r$
form a single conjugacy class.
$\mathfrak {A}_r$
form a single conjugacy class.
Proof of Theorem 1.3.
Let G be a subgroup of
![]() $S_{\Omega }$
, where
$S_{\Omega }$
, where
![]() $|\Omega |=n$
, and let
$|\Omega |=n$
, and let
![]() ${G \in \mathfrak {A}_q\mathfrak {A}_r}$
. Then
${G \in \mathfrak {A}_q\mathfrak {A}_r}$
. Then
![]() $G = Q \rtimes R$
, where Q is an elementary abelian Sylow q-subgroup, R is an elementary abelian Sylow r-subgroup and
$G = Q \rtimes R$
, where Q is an elementary abelian Sylow q-subgroup, R is an elementary abelian Sylow r-subgroup and
![]() $|G| = q^\beta r^\gamma $
, with
$|G| = q^\beta r^\gamma $
, with
![]() $\beta $
,
$\beta $
,
![]() $\gamma \in \mathbb {N}$
. Let M be a minimal normal subgroup of G. Then M is an elementary abelian u-group. Clearly,
$\gamma \in \mathbb {N}$
. Let M be a minimal normal subgroup of G. Then M is an elementary abelian u-group. Clearly,
![]() $|M|=u^{k}$
for some
$|M|=u^{k}$
for some
![]() $k> 1$
and for some prime
$k> 1$
and for some prime
![]() $u \in \{q,r\}$
.
$u \in \{q,r\}$
.
Now
![]() $F(G)$
, the Fitting subgroup of G, is an abelian normal subgroup of G and so, by the O’Nan–Scott theorem,
$F(G)$
, the Fitting subgroup of G, is an abelian normal subgroup of G and so, by the O’Nan–Scott theorem,
![]() $n=|M|=|F(G)|$
. However,
$n=|M|=|F(G)|$
. However,
![]() $M \leq F(G)$
, therefore,
$M \leq F(G)$
, therefore,
![]() ${M=F(G)}$
and
${M=F(G)}$
and
![]() $n=u^k$
. If
$n=u^k$
. If
![]() $\beta \geq 1$
, then
$\beta \geq 1$
, then
![]() $Q \leq F(G)$
and we have
$Q \leq F(G)$
and we have
![]() $n= q^{\beta } = u^k$
and
$n= q^{\beta } = u^k$
and
![]() $M=F(G) = Q$
. Let
$M=F(G) = Q$
. Let
![]() $H=G_{\alpha }$
be the stabiliser of an
$H=G_{\alpha }$
be the stabiliser of an
![]() $\alpha \in \Omega $
. By [Reference Blackburn, Neumann and Venkataraman1, Proposition 6.13], G is a semidirect product of M by H and H acts faithfully by conjugation on M. By Maschke’s theorem, M is completely reducible. However, M is a minimal normal subgroup of G, so M is a nontrivial irreducible
$\alpha \in \Omega $
. By [Reference Blackburn, Neumann and Venkataraman1, Proposition 6.13], G is a semidirect product of M by H and H acts faithfully by conjugation on M. By Maschke’s theorem, M is completely reducible. However, M is a minimal normal subgroup of G, so M is a nontrivial irreducible
![]() $\mathbb {F}_{q}H$
-module and H is an abelian group acting faithfully on M. By [Reference Venkataraman14, Corollary 4.1],
$\mathbb {F}_{q}H$
-module and H is an abelian group acting faithfully on M. By [Reference Venkataraman14, Corollary 4.1],
![]() $H\cong C_{r}$
and
$H\cong C_{r}$
and
![]() $ \beta = \dim M = \text {order } q \bmod r$
and the result follows. If
$ \beta = \dim M = \text {order } q \bmod r$
and the result follows. If
![]() $\gamma = 0$
or
$\gamma = 0$
or
![]() $\beta = 0$
, then
$\beta = 0$
, then
![]() $|G|$
is a power of u, where
$|G|$
is a power of u, where
![]() $u \in \{q, r\}$
. Thus, G is a primitive subgroup that is also in
$u \in \{q, r\}$
. Thus, G is a primitive subgroup that is also in
![]() $\mathfrak {A}_u$
and the result follows by Lemma 2.1.
$\mathfrak {A}_u$
and the result follows by Lemma 2.1.
It is clear from these results that if
![]() $S_n$
has a primitive subgroup G of order
$S_n$
has a primitive subgroup G of order
![]() $q^{\beta }r^{\gamma }$
in
$q^{\beta }r^{\gamma }$
in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
, then n must be r or q and G is cyclic with
$\mathfrak {A}_q\mathfrak {A}_r$
, then n must be r or q and G is cyclic with
![]() $|G|=n$
, or
$|G|=n$
, or
![]() $n=q^{\beta }$
and G is a semi-direct product of an elementary abelian q-group of order
$n=q^{\beta }$
and G is a semi-direct product of an elementary abelian q-group of order
![]() $q^{\beta }$
by a cyclic group of order r. The limits imposed on n and the structure of such primitive subgroups gives the next result.
$q^{\beta }$
by a cyclic group of order r. The limits imposed on n and the structure of such primitive subgroups gives the next result.
Proof of Theorem 1.4.
Let G be a primitive subgroup of
![]() $S_{\Omega }$
that is in
$S_{\Omega }$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
, where
$\mathfrak {A}_q\mathfrak {A}_r$
, where
![]() $|\Omega | = n$
, and let
$|\Omega | = n$
, and let
![]() $|G|= q^{\beta }r^{\gamma }$
. Let M be a minimal normal subgroup of G. As seen in the proof of Theorem 1.3,
$|G|= q^{\beta }r^{\gamma }$
. Let M be a minimal normal subgroup of G. As seen in the proof of Theorem 1.3,
![]() $M = F(G)$
and
$M = F(G)$
and
![]() $n=|M|$
is either a power of q or r. If
$n=|M|$
is either a power of q or r. If
![]() $\gamma = 0$
or
$\gamma = 0$
or
![]() $\beta = 0$
, then
$\beta = 0$
, then
![]() $|G|$
is a power of u, where
$|G|$
is a power of u, where
![]() $u \in \{q, r\}$
. Thus, G is a primitive subgroup that is also in
$u \in \{q, r\}$
. Thus, G is a primitive subgroup that is also in
![]() $\mathfrak {A}_u$
and the result follows by Lemma 2.1.
$\mathfrak {A}_u$
and the result follows by Lemma 2.1.
We know the structure of G when
![]() $\beta \geq 1$
from the proof of Theorem 1.3. Hence, H can be regarded as a soluble r-subgroup of
$\beta \geq 1$
from the proof of Theorem 1.3. Hence, H can be regarded as a soluble r-subgroup of
![]() $\mathrm{GL}(\beta ,q)$
and it is not difficult to show that the conjugacy class of G in
$\mathrm{GL}(\beta ,q)$
and it is not difficult to show that the conjugacy class of G in
![]() $S_{n}$
is determined by the conjugacy class of H in
$S_{n}$
is determined by the conjugacy class of H in
![]() $\mathrm{GL}(\beta ,q)$
. Let S be a Singer subgroup of
$\mathrm{GL}(\beta ,q)$
. Let S be a Singer subgroup of
![]() $\mathrm{GL}(\beta ,q)$
, so that
$\mathrm{GL}(\beta ,q)$
, so that
![]() $|S| = q^{\beta }-1$
. Now,
$|S| = q^{\beta }-1$
. Now,
![]() $|H| =r$
and r divides
$|H| =r$
and r divides
![]() $|S|$
. Further,
$|S|$
. Further,
![]() $\gcd (|\mathrm{GL}(\beta ,q)|/|S|, r)=1$
as
$\gcd (|\mathrm{GL}(\beta ,q)|/|S|, r)=1$
as
![]() $\beta $
is the least positive integer such that
$\beta $
is the least positive integer such that
![]() ${r \mid q^{\beta }-1}$
. From [Reference Hestenes3, Theorem 2.11],
${r \mid q^{\beta }-1}$
. From [Reference Hestenes3, Theorem 2.11],
![]() $H^{x} \leq S$
for some
$H^{x} \leq S$
for some
![]() $x \in \mathrm{GL}(\beta ,q)$
. Since all Singer subgroups are conjugate in
$x \in \mathrm{GL}(\beta ,q)$
. Since all Singer subgroups are conjugate in
![]() $\mathrm{GL}(\beta ,q)$
, the result follows.
$\mathrm{GL}(\beta ,q)$
, the result follows.
3. Subgroups of
 $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
 $\mathfrak {A}_r$
$\mathfrak {A}_r$
In this section, we prove results that give us a bound on the number of conjugacy classes of the subgroups that are maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_r$
. The limits on the structure of such groups ensures that if they exist, they form a single conjugacy class.
$\mathfrak {A}_r$
. The limits on the structure of such groups ensures that if they exist, they form a single conjugacy class.
Lemma 3.1. The number of conjugacy classes of irreducible subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_r$
is at most
$\mathfrak {A}_r$
is at most
![]() $1$
.
$1$
.
Proof. Let G be a nontrivial irreducible subgroup of
![]() $\mathrm{GL}(\alpha , s)$
that is also in
$\mathrm{GL}(\alpha , s)$
that is also in
![]() $\mathfrak {A}_r$
. Then G is an elementary abelian r-group of order
$\mathfrak {A}_r$
. Then G is an elementary abelian r-group of order
![]() $r^{\gamma }$
, say, where
$r^{\gamma }$
, say, where
![]() $\gamma \in \mathbb {N}$
. Since G is a faithful abelian irreducible subgroup of
$\gamma \in \mathbb {N}$
. Since G is a faithful abelian irreducible subgroup of
![]() $\mathrm{GL}(\alpha , s)$
whose order is coprime to s, it follows that G is cyclic [Reference Venkataraman14, Lemma 4.2]. Thus,
$\mathrm{GL}(\alpha , s)$
whose order is coprime to s, it follows that G is cyclic [Reference Venkataraman14, Lemma 4.2]. Thus,
![]() $|G|=r$
and
$|G|=r$
and
![]() $\alpha = d$
, where
$\alpha = d$
, where
![]() $d= \text {order } s \bmod r$
. From [Reference Short11, Theorem 2.3.3], the irreducible cyclic subgroups of order r in
$d= \text {order } s \bmod r$
. From [Reference Short11, Theorem 2.3.3], the irreducible cyclic subgroups of order r in
![]() $\mathrm{GL}(\alpha , s)$
lie in a single conjugacy class.
$\mathrm{GL}(\alpha , s)$
lie in a single conjugacy class.
Proposition 3.2. The number of conjugacy classes of subgroups that are maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_r$
is at most
$\mathfrak {A}_r$
is at most
![]() $1$
.
$1$
.
Proof. Let G be maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_r$
. Since
$\mathfrak {A}_r$
. Since
![]() $\text {char}(\mathbb {F}_{p}) = t \nmid |G|$
, by Maschke’s theorem, we can find groups
$\text {char}(\mathbb {F}_{p}) = t \nmid |G|$
, by Maschke’s theorem, we can find groups
![]() $G_i$
such that
$G_i$
such that
![]() $G \leq G_{1} \times G_{2} \times \cdots \times G_{k} = \hat {G} \leq \mathrm{GL}(\alpha , s)$
, where for each i, the group
$G \leq G_{1} \times G_{2} \times \cdots \times G_{k} = \hat {G} \leq \mathrm{GL}(\alpha , s)$
, where for each i, the group
![]() $G_i$
is a (maximal) irreducible subgroup of
$G_i$
is a (maximal) irreducible subgroup of
![]() $\mathrm{GL}(\alpha _i, s)$
that is also in
$\mathrm{GL}(\alpha _i, s)$
that is also in
![]() $\mathfrak {A}_r$
. Further,
$\mathfrak {A}_r$
. Further,
![]() $\alpha = \alpha _1 + \cdots + \alpha _k$
. Clearly,
$\alpha = \alpha _1 + \cdots + \alpha _k$
. Clearly,
![]() $G_i \cong C_r$
and
$G_i \cong C_r$
and
![]() $\alpha _i = d = \text {order } s \bmod r$
for each i. Thus, we must have
$\alpha _i = d = \text {order } s \bmod r$
for each i. Thus, we must have
![]() $\alpha = dk$
and by the maximality of G, we have
$\alpha = dk$
and by the maximality of G, we have
![]() $G = \hat {G}$
. Further, the conjugacy classes of
$G = \hat {G}$
. Further, the conjugacy classes of
![]() $G_i$
in
$G_i$
in
![]() $\mathrm{GL}(\alpha _i, s)$
determine the conjugacy class of G in
$\mathrm{GL}(\alpha _i, s)$
determine the conjugacy class of G in
![]() $\mathrm{GL}(\alpha , s)$
.
$\mathrm{GL}(\alpha , s)$
.
So if d does not divide
![]() $\alpha $
, then
$\alpha $
, then
![]() $\mathrm{GL}(\alpha , s)$
cannot have an elementary abelian r-subgroup. If
$\mathrm{GL}(\alpha , s)$
cannot have an elementary abelian r-subgroup. If
![]() $d \mid \alpha $
, then any G that is maximal amongst subgroups of
$d \mid \alpha $
, then any G that is maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_r$
must have order
$\mathfrak {A}_r$
must have order
![]() $r^{k}$
, where
$r^{k}$
, where
![]() $k = \alpha /d$
. By Lemma 3.1, all such groups form a single conjugacy class.
$k = \alpha /d$
. By Lemma 3.1, all such groups form a single conjugacy class.
4. Subgroups of
 $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
 $\mathfrak {A}_q\mathfrak {A}_r$
$\mathfrak {A}_q\mathfrak {A}_r$
We prove results that give a bound on the order of subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
and also a bound for the number of conjugacy classes of subgroups that are maximal amongst subgroups of
$\mathfrak {A}_q\mathfrak {A}_r$
and also a bound for the number of conjugacy classes of subgroups that are maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. Theorem 1.5 is proved in this section.
$\mathfrak {A}_q\mathfrak {A}_r$
. Theorem 1.5 is proved in this section.
Proposition 4.1. Let G be a subgroup of
![]() $\mathrm{GL}(\alpha , s)$
that is in
$\mathrm{GL}(\alpha , s)$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
.
$\mathfrak {A}_q\mathfrak {A}_r$
.
-
(i) Let
 $m = |F(G)|$
. If G is primitive, then
$m = |F(G)|$
. If G is primitive, then
 $|G| \leq cm$
, where
$|G| \leq cm$
, where
 $c = {\mathrm{order}} \ s \bmod m$
and
$c = {\mathrm{order}} \ s \bmod m$
and
 $c \mid \alpha $
. Further, m is either r or q or
$c \mid \alpha $
. Further, m is either r or q or
 $qr$
.
$qr$
. -
(ii)
 $|G| \leq {(6^{1/2})}^{\alpha - 1} {d}^{\alpha }$
, where
$|G| \leq {(6^{1/2})}^{\alpha - 1} {d}^{\alpha }$
, where
 $d = \min \{ qr, s \}$
.
$d = \min \{ qr, s \}$
.
Proof. Let
![]() $V = (\mathbb {F}_{s})^{\alpha }$
. Let G be a primitive subgroup of
$V = (\mathbb {F}_{s})^{\alpha }$
. Let G be a primitive subgroup of
![]() $\mathrm{GL}(\alpha , s)$
that is in
$\mathrm{GL}(\alpha , s)$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
and let
$\mathfrak {A}_q\mathfrak {A}_r$
and let
![]() $|G| = q^{\beta } r^{\gamma }$
, where
$|G| = q^{\beta } r^{\gamma }$
, where
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are natural numbers. If
$\gamma $
are natural numbers. If
![]() $\beta = 0$
or
$\beta = 0$
or
![]() $\gamma = 0$
, then the result follows from Lemma 3.1. Assume that
$\gamma = 0$
, then the result follows from Lemma 3.1. Assume that
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are at least 1. Let
$\gamma $
are at least 1. Let
![]() $F = F(G)$
be the Fitting subgroup of G. Since
$F = F(G)$
be the Fitting subgroup of G. Since
![]() $G \in \mathfrak {A}_q\mathfrak {A}_r$
, it follows that F is abelian and
$G \in \mathfrak {A}_q\mathfrak {A}_r$
, it follows that F is abelian and
![]() $|F|=q^{\beta }r^{\gamma _1} =m$
, where
$|F|=q^{\beta }r^{\gamma _1} =m$
, where
![]() $\gamma _1 \leq \gamma $
. By Clifford’s theorem, since G is primitive,
$\gamma _1 \leq \gamma $
. By Clifford’s theorem, since G is primitive,
![]() $V = X_{1} \oplus X_{2} \oplus \cdots \oplus X_{a}$
as an F-module, where the
$V = X_{1} \oplus X_{2} \oplus \cdots \oplus X_{a}$
as an F-module, where the
![]() $X_{i}$
are conjugates of X, an irreducible
$X_{i}$
are conjugates of X, an irreducible
![]() $\mathbb {F}_{s}F$
-submodule of V. Note that F acts faithfully on X.
$\mathbb {F}_{s}F$
-submodule of V. Note that F acts faithfully on X.
Let E be the subalgebra generated by F in
![]() $\text {End}(V)$
. The
$\text {End}(V)$
. The
![]() $X_{i}$
are conjugates of X, so E acts faithfully and irreducibly on X and E is commutative. By [Reference Blackburn, Neumann and Venkataraman1, Proposition 8.2 and Theorem 8.3], E is a field. Thus,
$X_{i}$
are conjugates of X, so E acts faithfully and irreducibly on X and E is commutative. By [Reference Blackburn, Neumann and Venkataraman1, Proposition 8.2 and Theorem 8.3], E is a field. Thus,
![]() $E \cong \mathbb {F}_{s^{c}}$
as an
$E \cong \mathbb {F}_{s^{c}}$
as an
![]() $\mathbb {F}_{s}F$
-module, where
$\mathbb {F}_{s}F$
-module, where
![]() $c = \dim (X)$
and
$c = \dim (X)$
and
![]() $\alpha = ac$
. Note that F is an abelian group of order m acting faithfully and irreducibly on X. Consequently, F is cyclic and c is the least positive integer such that
$\alpha = ac$
. Note that F is an abelian group of order m acting faithfully and irreducibly on X. Consequently, F is cyclic and c is the least positive integer such that
![]() $m \mid s^{c} -1 $
. Clearly,
$m \mid s^{c} -1 $
. Clearly,
![]() $m=q$
or
$m=q$
or
![]() $m=qr$
and so
$m=qr$
and so
![]() $\beta =1$
. It is not difficult to show that G acts on E by conjugation. Hence, there exists a homomorphism from G to
$\beta =1$
. It is not difficult to show that G acts on E by conjugation. Hence, there exists a homomorphism from G to
![]() $\text {Gal}_{\mathbb {F}_{s}}(E)$
. Let N be the kernel of this map. Then
$\text {Gal}_{\mathbb {F}_{s}}(E)$
. Let N be the kernel of this map. Then
![]() $N = C_{G}(E) \leq C_{G}(F) \leq F$
. However,
$N = C_{G}(E) \leq C_{G}(F) \leq F$
. However,
![]() $F \leq N$
. Hence,
$F \leq N$
. Hence,
![]() $F=N$
. So
$F=N$
. So
![]() ${G}/{F} \leq \text {Gal}_{\mathbb {F}_{s}}(E) \cong C_{c}$
and
${G}/{F} \leq \text {Gal}_{\mathbb {F}_{s}}(E) \cong C_{c}$
and
![]() $|G| \leq cm$
.
$|G| \leq cm$
.
Let G be an irreducible imprimitive subgroup of
![]() $\mathrm{GL}(\alpha , s)$
that is also in
$\mathrm{GL}(\alpha , s)$
that is also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. Then
$\mathfrak {A}_q\mathfrak {A}_r$
. Then
![]() $G \leq G_{1}\, \mathrm{wr} \,G_{2} \leq \mathrm{GL}(\alpha , s)$
, where
$G \leq G_{1}\, \mathrm{wr} \,G_{2} \leq \mathrm{GL}(\alpha , s)$
, where
![]() $G_{1}$
is a primitive subgroup of
$G_{1}$
is a primitive subgroup of
![]() $\mathrm{GL}(\alpha _1, s)$
that is in
$\mathrm{GL}(\alpha _1, s)$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
, and the group
$\mathfrak {A}_q\mathfrak {A}_r$
, and the group
![]() $G_{2}$
can be regarded as a transitive subgroup of
$G_{2}$
can be regarded as a transitive subgroup of
![]() $S_{k}$
that is in
$S_{k}$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. Further,
$\mathfrak {A}_q\mathfrak {A}_r$
. Further,
![]() $\alpha = \alpha _{1} k$
. By the previous part,
$\alpha = \alpha _{1} k$
. By the previous part,
![]() $|G_1| \leq c'm'$
, where
$|G_1| \leq c'm'$
, where
![]() $c' = \text {order}\ s \bmod m' $
and
$c' = \text {order}\ s \bmod m' $
and
![]() $m' = |F(G_1)|$
is either r or q or
$m' = |F(G_1)|$
is either r or q or
![]() $qr$
. Also
$qr$
. Also
![]() $c' \mid \alpha _1$
. By [Reference Venkataraman13, Proposition 2.1],
$c' \mid \alpha _1$
. By [Reference Venkataraman13, Proposition 2.1],
![]() $|G_2| \leq {(6^{1/2})}^{k-1}$
. Using
$|G_2| \leq {(6^{1/2})}^{k-1}$
. Using
![]() $c' \leq 2^{c'-1} \leq {(6^{1/2})}^{c' - 1}$
, we see that
$c' \leq 2^{c'-1} \leq {(6^{1/2})}^{c' - 1}$
, we see that
![]() $|G| \leq {(6^{1/2})}^{\alpha - 1} \, {(m')}^{k}$
. Since
$|G| \leq {(6^{1/2})}^{\alpha - 1} \, {(m')}^{k}$
. Since
![]() $m' \mid p^{c'} -1$
, we have
$m' \mid p^{c'} -1$
, we have
![]() ${(m')}^k \leq d^{\alpha }$
, where
${(m')}^k \leq d^{\alpha }$
, where
![]() $d = \min \{ qr, s \}$
.
$d = \min \{ qr, s \}$
.
Since t does not divide q or r, by Maschke’s theorem, any subgroup G of
![]() $\mathrm{GL}(\alpha , s)$
that is in
$\mathrm{GL}(\alpha , s)$
that is in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
will be completely reducible. Thus,
$\mathfrak {A}_q\mathfrak {A}_r$
will be completely reducible. Thus,
![]() $G \leq G_{1} \times \cdots \times G_{k} \leq \mathrm{GL}(\alpha , s)$
, where the
$G \leq G_{1} \times \cdots \times G_{k} \leq \mathrm{GL}(\alpha , s)$
, where the
![]() $G_{i}$
are irreducible subgroups of
$G_{i}$
are irreducible subgroups of
![]() $\mathrm{GL}(\alpha _i, s)$
that are in
$\mathrm{GL}(\alpha _i, s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
and
$\mathfrak {A}_q\mathfrak {A}_r$
and
![]() $\alpha = \alpha _{1} + \cdots + \alpha _{k}$
. Hence,
$\alpha = \alpha _{1} + \cdots + \alpha _{k}$
. Hence,
![]() $|G| \leq {(6^{1/2})}^{\alpha - 1} \, {d}^{\alpha }$
, where
$|G| \leq {(6^{1/2})}^{\alpha - 1} \, {d}^{\alpha }$
, where
![]() $d = \min \{ qr, s \}$
.
$d = \min \{ qr, s \}$
.
Proposition 4.2. There exist constants b and c such that the number of conjugacy classes of subgroups that are maximal amongst irreducible subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
![]() $ 2^{(b+c) ({\alpha }^2/\sqrt {\log \alpha }) + (5/6) \log \alpha + \log 6} s^{(3+c){\alpha }^2}$
provided
$ 2^{(b+c) ({\alpha }^2/\sqrt {\log \alpha }) + (5/6) \log \alpha + \log 6} s^{(3+c){\alpha }^2}$
provided
![]() $\alpha> 1$
.
$\alpha> 1$
.
Proof. Let G be a subgroup of
![]() $\mathrm{GL}(\alpha , s)$
that is maximal amongst irreducible subgroups of
$\mathrm{GL}(\alpha , s)$
that is maximal amongst irreducible subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. Let
$\mathfrak {A}_q\mathfrak {A}_r$
. Let
![]() $|G| = q^{\beta } r^{\gamma }$
, where
$|G| = q^{\beta } r^{\gamma }$
, where
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are natural numbers. If
$\gamma $
are natural numbers. If
![]() $\beta = 0$
or
$\beta = 0$
or
![]() $\gamma = 0$
, then the result follows from Lemma 3.1. Assume that
$\gamma = 0$
, then the result follows from Lemma 3.1. Assume that
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
are at least 1. Let
$\gamma $
are at least 1. Let
![]() $V = (\mathbb {F}_{s})^{\alpha }$
and
$V = (\mathbb {F}_{s})^{\alpha }$
and
![]() $F = F(G)$
, the Fitting subgroup of G. Then
$F = F(G)$
, the Fitting subgroup of G. Then
![]() $F=Q \times R_1$
, where Q is the unique Sylow q-subgroup of G and
$F=Q \times R_1$
, where Q is the unique Sylow q-subgroup of G and
![]() $R_1 \leq R$
, where R is a Sylow r-subgroup of G. So F is abelian and
$R_1 \leq R$
, where R is a Sylow r-subgroup of G. So F is abelian and
![]() $|F|=q^{\beta }r^{\gamma _1} =m$
, where
$|F|=q^{\beta }r^{\gamma _1} =m$
, where
![]() $\gamma _1 \leq \gamma $
.
$\gamma _1 \leq \gamma $
.
From Clifford’s theorem, regarding V as an
![]() $\mathbb {F}_{s}F$
-module,
$\mathbb {F}_{s}F$
-module,
![]() $V = Y_{1} \oplus Y_{2} \oplus \cdots \oplus Y_{l}$
, where
$V = Y_{1} \oplus Y_{2} \oplus \cdots \oplus Y_{l}$
, where
![]() $Y_{i} = k X_{i}$
for all i, and
$Y_{i} = k X_{i}$
for all i, and
![]() $X_{1}, \ldots , X_{l}$
are irreducible
$X_{1}, \ldots , X_{l}$
are irreducible
![]() $\mathbb {F}_{s}F$
-submodules of V. Further, for each
$\mathbb {F}_{s}F$
-submodules of V. Further, for each
![]() $i,j$
, there exists
$i,j$
, there exists
![]() $g_{ij} \in G$
such that
$g_{ij} \in G$
such that
![]() $g_{ij}X_{i} = X_{j}$
and, for
$g_{ij}X_{i} = X_{j}$
and, for
![]() $i=1, \ldots , l$
, the
$i=1, \ldots , l$
, the
![]() $X_{i}$
form a maximal set of pairwise nonisomorphic conjugates. Also, the action of G on the
$X_{i}$
form a maximal set of pairwise nonisomorphic conjugates. Also, the action of G on the
![]() $Y_{i}$
is transitive. It is not difficult to check that
$Y_{i}$
is transitive. It is not difficult to check that
![]() $ C_{F}(Y_{i}) = C_{F}(X_{i}) = K_i$
, say. Thus,
$ C_{F}(Y_{i}) = C_{F}(X_{i}) = K_i$
, say. Thus,
![]() $F/K_i$
acts faithfully on
$F/K_i$
acts faithfully on
![]() $Y_{i}$
and when its action is restricted to
$Y_{i}$
and when its action is restricted to
![]() $X_{i}$
, it acts faithfully and irreducibly on
$X_{i}$
, it acts faithfully and irreducibly on
![]() $X_{i}$
. Since
$X_{i}$
. Since
![]() $X_{i}$
is a nontrivial irreducible faithful
$X_{i}$
is a nontrivial irreducible faithful
![]() $\mathbb {F}_{s}F/K_i$
-module, and t is coprime to q and r, it follows that
$\mathbb {F}_{s}F/K_i$
-module, and t is coprime to q and r, it follows that
![]() $F/K_i$
is cyclic and
$F/K_i$
is cyclic and
![]() $\dim _{\mathbb {F}_{s}}(X_i) = d_i$
, where
$\dim _{\mathbb {F}_{s}}(X_i) = d_i$
, where
![]() $d_i$
is the least positive integer such that
$d_i$
is the least positive integer such that
![]() $m_i$
divides
$m_i$
divides
![]() $s^{d_i} -1$
, and where
$s^{d_i} -1$
, and where
![]() $m_i$
is the order of
$m_i$
is the order of
![]() $F/K_i$
. Since the
$F/K_i$
. Since the
![]() $X_i$
are conjugate,
$X_i$
are conjugate,
![]() $\dim _{\mathbb {F}_{s}}(X_i) = d_i = d$
for all i.
$\dim _{\mathbb {F}_{s}}(X_i) = d_i = d$
for all i.
Let
![]() $E_{i}$
be the subalgebra generated by
$E_{i}$
be the subalgebra generated by
![]() $F/K_i$
in
$F/K_i$
in
![]() $\text {End}_{{\mathbb{F}}_{s}}(Y_{i})$
. Note that
$\text {End}_{{\mathbb{F}}_{s}}(Y_{i})$
. Note that
![]() $E_{i}$
is commutative as
$E_{i}$
is commutative as
![]() $F/K_i$
is abelian. Further,
$F/K_i$
is abelian. Further,
![]() $X_{i}$
is a faithful irreducible
$X_{i}$
is a faithful irreducible
![]() $E_{i}$
-module. So
$E_{i}$
-module. So
![]() $E_{i}$
is simple and becomes a field such that
$E_{i}$
is simple and becomes a field such that
![]() $E_{i} \cong \mathbb{F}_{s{^d}}$
. We also observe that
$E_{i} \cong \mathbb{F}_{s{^d}}$
. We also observe that
![]() $\alpha = k l d$
.
$\alpha = k l d$
.
Let
![]() $k, l, d$
be fixed such that
$k, l, d$
be fixed such that
![]() $\alpha = kld$
. Next we find the number of choices for F up to conjugacy in
$\alpha = kld$
. Next we find the number of choices for F up to conjugacy in
![]() $\mathrm{GL}(V)$
. Clearly,
$\mathrm{GL}(V)$
. Clearly,
 $$ \begin{align*} F &\leq F/K_1 \times F/K_2 \times \cdots \times F/K_l \leq {E_1}^{*} \times {E_2}^{*} \times \cdots \times {E_l}^{*} \\ &\leq \mathrm{GL}(Y_{1}) \times \mathrm{GL}(Y_{2}) \times \cdots \times \mathrm{GL}(Y_{l}) \leq \mathrm{GL}(V), \end{align*} $$
$$ \begin{align*} F &\leq F/K_1 \times F/K_2 \times \cdots \times F/K_l \leq {E_1}^{*} \times {E_2}^{*} \times \cdots \times {E_l}^{*} \\ &\leq \mathrm{GL}(Y_{1}) \times \mathrm{GL}(Y_{2}) \times \cdots \times \mathrm{GL}(Y_{l}) \leq \mathrm{GL}(V), \end{align*} $$
where
![]() ${E_i}^*$
denotes the multiplicative group of the field
${E_i}^*$
denotes the multiplicative group of the field
![]() $E_i$
. Let
$E_i$
. Let
![]() $E = {E_1}^{*} \times {E_2}^{*} \times \cdots \times {E_l}^{*}$
. Then
$E = {E_1}^{*} \times {E_2}^{*} \times \cdots \times {E_l}^{*}$
. Then
![]() $|E|= (s^{d} - 1)^{l}$
. Regarding V as an
$|E|= (s^{d} - 1)^{l}$
. Regarding V as an
![]() $\mathbb{F}_{s}E$
-module,
$\mathbb{F}_{s}E$
-module,
![]() $V = kX_{1} \oplus kX_{2} \oplus \cdots \oplus kX_{l}$
, where
$V = kX_{1} \oplus kX_{2} \oplus \cdots \oplus kX_{l}$
, where
![]() $E_{i}^{*}$
acts faithfully and irreducibly on
$E_{i}^{*}$
acts faithfully and irreducibly on
![]() $X_{i}$
and
$X_{i}$
and
![]() $\dim _{E_{i}}(X_{i}) = 1$
for all i. Further, for
$\dim _{E_{i}}(X_{i}) = 1$
for all i. Further, for
![]() $i \neq j$
,
$i \neq j$
,
![]() $E_{i}^{*}$
acts trivially on
$E_{i}^{*}$
acts trivially on
![]() $X_{j}$
. It is not difficult to show that there is only one conjugacy class of subgroups of type E in
$X_{j}$
. It is not difficult to show that there is only one conjugacy class of subgroups of type E in
![]() $\mathrm{GL}(V)$
.
$\mathrm{GL}(V)$
.
So once
![]() $k,l$
and d are chosen such that
$k,l$
and d are chosen such that
![]() $\alpha = k l d$
, up to conjugacy, there is only one choice for E. Since E is a direct product of l isomorphic cyclic groups, any subgroup of E can be generated by l elements. In particular, F can be generated by l elements. So the number of choices for F as a subgroup of E is at most
$\alpha = k l d$
, up to conjugacy, there is only one choice for E. Since E is a direct product of l isomorphic cyclic groups, any subgroup of E can be generated by l elements. In particular, F can be generated by l elements. So the number of choices for F as a subgroup of E is at most
![]() $|E|^{l}= (s^{d} - 1)^{{l}^{2}}$
.
$|E|^{l}= (s^{d} - 1)^{{l}^{2}}$
.
Since, G acts transitively on
![]() $\{Y_{1},\ldots , Y_{l}\}$
, there exists a homomorphism
$\{Y_{1},\ldots , Y_{l}\}$
, there exists a homomorphism
![]() $\phi $
from G into
$\phi $
from G into
![]() $S_{l}$
. Let
$S_{l}$
. Let
![]() ${N} = \ker (\phi ) = \{g \in G \mid gY_{i} = Y_{i}\text { for all } i \}$
. Clearly,
${N} = \ker (\phi ) = \{g \in G \mid gY_{i} = Y_{i}\text { for all } i \}$
. Clearly,
![]() $F \leq {N}$
and
$F \leq {N}$
and
![]() $G/{N}$
is a transitive subgroup of
$G/{N}$
is a transitive subgroup of
![]() $S_{l}$
that is in
$S_{l}$
that is in
![]() $\mathfrak {A}_r$
. If
$\mathfrak {A}_r$
. If
![]() $g \in {N}$
, then
$g \in {N}$
, then
![]() $gE_{i}g^{-1}=E_{i}$
. Thus, there exists a homomorphism
$gE_{i}g^{-1}=E_{i}$
. Thus, there exists a homomorphism
![]() $\psi _{i}: {N} \rightarrow \text {Gal}_{\mathbb {F}_{s}}(E_{i})$
. This induces a homomorphism
$\psi _{i}: {N} \rightarrow \text {Gal}_{\mathbb {F}_{s}}(E_{i})$
. This induces a homomorphism
![]() $\psi $
from N to
$\psi $
from N to
![]() $\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
such that
$\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
such that
![]() $\ker (\psi ) = \bigcap _{i=1}^{l} N_{i} = F$
, where
$\ker (\psi ) = \bigcap _{i=1}^{l} N_{i} = F$
, where
![]() $N_{i} = \ker (\psi _i) = C_{N}(E_{i})$
. So
$N_{i} = \ker (\psi _i) = C_{N}(E_{i})$
. So
![]() ${N}/F$
is isomorphic to a subgroup of
${N}/F$
is isomorphic to a subgroup of
![]() $\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
. Since
$\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
. Since
![]() $\text {Gal}_{\mathbb {F}_{s}}(E_{i}) \cong C_{d}$
for every i, it follows that
$\text {Gal}_{\mathbb {F}_{s}}(E_{i}) \cong C_{d}$
for every i, it follows that
![]() ${N}/F$
can be generated by l elements.
${N}/F$
can be generated by l elements.
Let
![]() $T=\mathrm{GL}(\alpha , s)$
. Let
$T=\mathrm{GL}(\alpha , s)$
. Let
![]() $\hat {N}=\{x \in N_{T}{(F)} \mid xY_{i}=Y_{i} \ \text {for all}\ i \}$
. Then
$\hat {N}=\{x \in N_{T}{(F)} \mid xY_{i}=Y_{i} \ \text {for all}\ i \}$
. Then
![]() $F \leq N \leq \hat {N} \leq N_{T}{(F)}$
. We will find the number of choices for N as a subgroup of
$F \leq N \leq \hat {N} \leq N_{T}{(F)}$
. We will find the number of choices for N as a subgroup of
![]() $\hat {N}$
, given that F has been chosen. The group
$\hat {N}$
, given that F has been chosen. The group
![]() $\hat {N}$
acts by conjugation on
$\hat {N}$
acts by conjugation on
![]() $E_{i}$
and fixes the elements of
$E_{i}$
and fixes the elements of
![]() $\mathbb {F}_s$
. So we have a homomorphism
$\mathbb {F}_s$
. So we have a homomorphism
![]() $\rho _{i}: \hat {N} \rightarrow \text {Gal}_{\mathbb {F}_{s}}(E_{i})$
with kernel
$\rho _{i}: \hat {N} \rightarrow \text {Gal}_{\mathbb {F}_{s}}(E_{i})$
with kernel
![]() $C_{\hat {N}}{(E_{i})}$
. Define
$C_{\hat {N}}{(E_{i})}$
. Define
![]() $C = \bigcap _{i=1}^{l} C_{\hat {N}}{(E_{i})}$
. Note that
$C = \bigcap _{i=1}^{l} C_{\hat {N}}{(E_{i})}$
. Note that
![]() $N \cap C = F$
. Also,
$N \cap C = F$
. Also,
![]() $\hat {N}/C$
is isomorphic to a subgroup of
$\hat {N}/C$
is isomorphic to a subgroup of
![]() $\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
, where each
$\text {Gal}_{\mathbb {F}_{s}}(E_{1}) \times \text {Gal}_{\mathbb {F}_{s}}(E_{2}) \times \cdots \times \text {Gal}_{\mathbb {F}_{s}}(E_{l})$
, where each
![]() $\text {Gal}_{\mathbb {F}_{s}}(E_{i}) $
is isomorphic to
$\text {Gal}_{\mathbb {F}_{s}}(E_{i}) $
is isomorphic to
![]() $C_{d}$
. So
$C_{d}$
. So
![]() $|\hat {N}/C| \leq d^{l}$
. Clearly, C centralises
$|\hat {N}/C| \leq d^{l}$
. Clearly, C centralises
![]() $E_{i}$
for each i. Therefore, there exists a homomorphism from C into
$E_{i}$
for each i. Therefore, there exists a homomorphism from C into
![]() $\mathrm{GL}_{E_{i}}{(Y_{i})}$
for each i. Hence, C is isomorphic to a subgroup of
$\mathrm{GL}_{E_{i}}{(Y_{i})}$
for each i. Hence, C is isomorphic to a subgroup of
![]() $\mathrm{GL}_{E_{1}}(Y_{1}) \times \mathrm{GL}_{E_{2}}(Y_{2}) \times \cdots \times \mathrm{GL}_{E_{l}}(Y_{l})$
. As
$\mathrm{GL}_{E_{1}}(Y_{1}) \times \mathrm{GL}_{E_{2}}(Y_{2}) \times \cdots \times \mathrm{GL}_{E_{l}}(Y_{l})$
. As
![]() $\dim _{\mathbb {E}_{i}}(Y_i) = k$
and
$\dim _{\mathbb {E}_{i}}(Y_i) = k$
and
![]() $E_{i} \cong \mathbb{F}_{s^{d}}$
for all i, it follows that
$E_{i} \cong \mathbb{F}_{s^{d}}$
for all i, it follows that
![]() $|C| \leq s^{dk^{2}l}$
. Hence,
$|C| \leq s^{dk^{2}l}$
. Hence,
![]() $|\hat {N}| \leq d^{l}s^{dk^{2}l}$
.
$|\hat {N}| \leq d^{l}s^{dk^{2}l}$
.
Now
![]() $NC/C \cong N/(N \cap C) = N/F$
. So
$NC/C \cong N/(N \cap C) = N/F$
. So
![]() $NC/C$
can be generated by l elements since
$NC/C$
can be generated by l elements since
![]() $N/F$
can be generated by l elements. However,
$N/F$
can be generated by l elements. However,
![]() $|\hat {N}/C| \leq d^{l}$
, therefore, there are at most
$|\hat {N}/C| \leq d^{l}$
, therefore, there are at most
![]() $d^{l^{2}}$
choices for
$d^{l^{2}}$
choices for
![]() $NC/C$
as a subgroup of
$NC/C$
as a subgroup of
![]() $\hat {N}/C$
. Once we make a choice for
$\hat {N}/C$
. Once we make a choice for
![]() $NC/C$
as a subgroup of
$NC/C$
as a subgroup of
![]() $\hat {N}/C$
, we choose a set of l generators for
$\hat {N}/C$
, we choose a set of l generators for
![]() $NC/C$
. As
$NC/C$
. As
![]() $N \cap C = F$
, we see that N is determined as a subgroup of
$N \cap C = F$
, we see that N is determined as a subgroup of
![]() $\hat {N}$
by F and l other elements that map to the chosen generating set of
$\hat {N}$
by F and l other elements that map to the chosen generating set of
![]() $NC/C$
. We have
$NC/C$
. We have
![]() $|C|$
choices for an element of
$|C|$
choices for an element of
![]() $\hat {N}$
that maps to any fixed element of
$\hat {N}$
that maps to any fixed element of
![]() $\hat {N}/C$
. Thus, there are at most
$\hat {N}/C$
. Thus, there are at most
![]() $|C|^{l}$
choices for N as a subgroup of
$|C|^{l}$
choices for N as a subgroup of
![]() $\hat {N}$
once
$\hat {N}$
once
![]() $NC/C$
has been chosen. So we have at most
$NC/C$
has been chosen. So we have at most
![]() $d^{l^{2}}(s^{{dk^{2}l}})^{l} = d^{l^{2}}s^{dk^{2}l^{2}}$
choices for N as a subgroup of
$d^{l^{2}}(s^{{dk^{2}l}})^{l} = d^{l^{2}}s^{dk^{2}l^{2}}$
choices for N as a subgroup of
![]() $\hat {N}$
, once F is fixed.
$\hat {N}$
, once F is fixed.
Next we find the number of choices for G given that F and N are fixed as subgroups of T and
![]() $\hat {N} \leq T$
, respectively. Let
$\hat {N} \leq T$
, respectively. Let
![]() $\hat {Y}=\{y \in N_{T}{(F)} \mid y \text { permutes the } Y_i \}$
. Then
$\hat {Y}=\{y \in N_{T}{(F)} \mid y \text { permutes the } Y_i \}$
. Then
![]() $F \leq G \leq \hat {Y} \leq N_{T}{(F)} \leq \mathrm{GL}(V)$
. Also there exists a homomorphism from
$F \leq G \leq \hat {Y} \leq N_{T}{(F)} \leq \mathrm{GL}(V)$
. Also there exists a homomorphism from
![]() $\hat {Y}$
to
$\hat {Y}$
to
![]() $S_{l}$
with kernel
$S_{l}$
with kernel
![]() ${\{y \in \hat {Y} \mid yY_{i} = Y_{i} \text { for all } i\} = \hat {N}}$
. Thus,
${\{y \in \hat {Y} \mid yY_{i} = Y_{i} \text { for all } i\} = \hat {N}}$
. Thus,
![]() $\hat {Y}/\hat {N}$
may be regarded as a subgroup of
$\hat {Y}/\hat {N}$
may be regarded as a subgroup of
![]() $S_{l}$
. However,
$S_{l}$
. However,
![]() $G \cap \hat {N} = N$
. Thus,
$G \cap \hat {N} = N$
. Thus,
![]() $G/N = G/(G \cap \hat {N}) \cong G\hat {N}/\hat {N}$
. So
$G/N = G/(G \cap \hat {N}) \cong G\hat {N}/\hat {N}$
. So
![]() ${G/N \cong G\hat {N}/\hat {N} \leq \hat {Y}/\hat {N} \leq S_{l}}$
. Note that
${G/N \cong G\hat {N}/\hat {N} \leq \hat {Y}/\hat {N} \leq S_{l}}$
. Note that
![]() $G/N$
is a transitive subgroup of
$G/N$
is a transitive subgroup of
![]() $S_{l}$
that is in
$S_{l}$
that is in
![]() $ {\mathfrak {A}_{\mathrm{r}}}$
. By [Reference Lucchini5, Theorem 1], there exists a constant b such that
$ {\mathfrak {A}_{\mathrm{r}}}$
. By [Reference Lucchini5, Theorem 1], there exists a constant b such that
![]() $S_{l}$
has at most
$S_{l}$
has at most
![]() $ 2^{bl^{2} / {\sqrt {\log l}}}$
transitive subgroups for
$ 2^{bl^{2} / {\sqrt {\log l}}}$
transitive subgroups for
![]() $l>1$
. Hence, the number of choices for
$l>1$
. Hence, the number of choices for
![]() $G\hat {N}/\hat {N}$
as a subgroup of
$G\hat {N}/\hat {N}$
as a subgroup of
![]() $\hat {Y}/\hat {N}$
is at most
$\hat {Y}/\hat {N}$
is at most
![]() $ 2^{bl^{2} / {\sqrt {\log l}}}$
.
$ 2^{bl^{2} / {\sqrt {\log l}}}$
.
By [Reference Lucchini, Menegazzo and Morigi6, Theorem 2], there exists a constant c such that any transitive permutation group of finite degree greater than
![]() $1$
can be generated by
$1$
can be generated by
![]() $\lfloor cl/\sqrt {\log l}\rfloor $
generators. Thus,
$\lfloor cl/\sqrt {\log l}\rfloor $
generators. Thus,
![]() $G\hat {N}/\hat {N}$
can be generated by
$G\hat {N}/\hat {N}$
can be generated by
![]() $\lfloor cl/\sqrt {\log l}\rfloor $
generators for
$\lfloor cl/\sqrt {\log l}\rfloor $
generators for
![]() $l> 1$
. Once a choice for
$l> 1$
. Once a choice for
![]() $G\hat {N}/\hat {N}$
is made as a subgroup of
$G\hat {N}/\hat {N}$
is made as a subgroup of
![]() $\hat {Y}/\hat {N}$
and
$\hat {Y}/\hat {N}$
and
![]() $\lfloor cl/\sqrt {\log l}\rfloor $
generators are chosen for
$\lfloor cl/\sqrt {\log l}\rfloor $
generators are chosen for
![]() $G\hat {N}/\hat {N}$
in
$G\hat {N}/\hat {N}$
in
![]() $\hat {Y}/\hat {N}$
, then G is determined as a subgroup of
$\hat {Y}/\hat {N}$
, then G is determined as a subgroup of
![]() $\hat {Y}$
by
$\hat {Y}$
by
![]() $\hat {N}$
and the elements of
$\hat {N}$
and the elements of
![]() $\hat {Y}$
that map to the
$\hat {Y}$
that map to the
![]() $\lfloor cl/\sqrt {\log l}\rfloor $
generators chosen for
$\lfloor cl/\sqrt {\log l}\rfloor $
generators chosen for
![]() $G\hat {N}/\hat {N}$
. So we have at most
$G\hat {N}/\hat {N}$
. So we have at most
![]() $|\hat {N}|^{\lfloor cl/\sqrt {\log l}\rfloor }$
choices for G as a subgroup of
$|\hat {N}|^{\lfloor cl/\sqrt {\log l}\rfloor }$
choices for G as a subgroup of
![]() $\hat {Y}$
once a choice of
$\hat {Y}$
once a choice of
![]() $G\hat {N}/\hat {N}$
in
$G\hat {N}/\hat {N}$
in
![]() $\hat {Y}/\hat {N}$
is fixed. Hence, there are
$\hat {Y}/\hat {N}$
is fixed. Hence, there are
choices for G as a subgroup of
![]() $\hat {Y}$
assuming that choices for F and N have been made. Putting together all these estimates, the number of conjugacy classes of subgroups that are maximal amongst irreducible subgroups of
$\hat {Y}$
assuming that choices for F and N have been made. Putting together all these estimates, the number of conjugacy classes of subgroups that are maximal amongst irreducible subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
 $$ \begin{align*} \sum_{(k,l,d)}^{} {(s^{d} - 1)^{{l}^{2}} d^{l^{2}} s^{dk^{2}l^{2}} {2^{bl^{2} / {\sqrt{\log l}}}} {d^{cl^{2}/ \sqrt{\log l}}} {s^{{cdk^{2}l^{2}}/\sqrt{\log l}}}}, \end{align*} $$
$$ \begin{align*} \sum_{(k,l,d)}^{} {(s^{d} - 1)^{{l}^{2}} d^{l^{2}} s^{dk^{2}l^{2}} {2^{bl^{2} / {\sqrt{\log l}}}} {d^{cl^{2}/ \sqrt{\log l}}} {s^{{cdk^{2}l^{2}}/\sqrt{\log l}}}}, \end{align*} $$
where
![]() $(k,l,d)$
ranges over ordered triples of natural numbers which satisfy
$(k,l,d)$
ranges over ordered triples of natural numbers which satisfy
![]() $\alpha = k l d$
and
$\alpha = k l d$
and
![]() $l>1$
. We simplify the above expression as follows. Writing
$l>1$
. We simplify the above expression as follows. Writing
![]() $\alpha = k l d$
,
$\alpha = k l d$
,
Since
![]() $x/\sqrt {\log x}$
is increasing for
$x/\sqrt {\log x}$
is increasing for
![]() $x> e^{1/2}$
, we have
$x> e^{1/2}$
, we have
![]() $l/\sqrt {\log l} \leq \alpha /\sqrt {\log \alpha }$
for
$l/\sqrt {\log l} \leq \alpha /\sqrt {\log \alpha }$
for
![]() $l \geq 2$
. Thus,
$l \geq 2$
. Thus,
![]() $2^{bl^{2} / {\sqrt {\log l}}} d^{cl^{2}/ \sqrt {\log l}} \leq 2^{(b + c) {\alpha }^2/\sqrt {\log \alpha }}$
.
$2^{bl^{2} / {\sqrt {\log l}}} d^{cl^{2}/ \sqrt {\log l}} \leq 2^{(b + c) {\alpha }^2/\sqrt {\log \alpha }}$
.
There are at most
![]() $2^{({5}/{6})\log \alpha +\log 6}$
choices for
$2^{({5}/{6})\log \alpha +\log 6}$
choices for
![]() $(k,l,d)$
. Thus, there exist constants b and c such that the number of conjugacy classes of subgroups that are maximal amongst irreducible subgroups of
$(k,l,d)$
. Thus, there exist constants b and c such that the number of conjugacy classes of subgroups that are maximal amongst irreducible subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are in
$\mathrm{GL}(\alpha , s)$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
provided
![]() $\alpha> 1$
.
$\alpha> 1$
.
Theorem 1.5 follows as a corollary to Proposition 4.2.
Proof of Theorem 1.5.
Let G be maximal amongst subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
. As the characteristic of
$\mathfrak {A}_q\mathfrak {A}_r$
. As the characteristic of
![]() $\mathbb {F}_{s} = t$
and
$\mathbb {F}_{s} = t$
and
![]() $t \nmid |G|$
, by Maschke’s theorem,
$t \nmid |G|$
, by Maschke’s theorem,
![]() $G \leq \hat {G_{1}}\times \cdots \times \hat {G_{k}} \leq \mathrm{GL}(\alpha , s)$
, where the
$G \leq \hat {G_{1}}\times \cdots \times \hat {G_{k}} \leq \mathrm{GL}(\alpha , s)$
, where the
![]() $\hat {G_{i}}$
are maximal among irreducible subgroups of
$\hat {G_{i}}$
are maximal among irreducible subgroups of
![]() $\mathrm{GL}(\alpha _{i}, p)$
that are also in
$\mathrm{GL}(\alpha _{i}, p)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
, and where
$\mathfrak {A}_q\mathfrak {A}_r$
, and where
![]() $\alpha = \alpha _{1} + \cdots + \alpha _{k}$
. By the maximality of G, we have
$\alpha = \alpha _{1} + \cdots + \alpha _{k}$
. By the maximality of G, we have
![]() $G = \hat {G_{1}}\times \cdots \times \hat {G_{k}}$
.
$G = \hat {G_{1}}\times \cdots \times \hat {G_{k}}$
.
The conjugacy classes of
![]() $\hat {G_{i}} \in \mathrm{GL}(\alpha _{i}, s)$
determine the conjugacy class of
$\hat {G_{i}} \in \mathrm{GL}(\alpha _{i}, s)$
determine the conjugacy class of
![]() ${G \in \mathrm{GL}(\alpha , s)}$
. So by Proposition 4.2, the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
${G \in \mathrm{GL}(\alpha , s)}$
. So by Proposition 4.2, the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
 $$ \begin{align*} \sum_{(\alpha)} \prod_{i=1}^{k} 2^{(b+c) ({\alpha_i}^2/\sqrt{\log \alpha_i}) + (5/6) \log \alpha_i + \log6} s^{(3+c){\alpha_i}^2},\end{align*} $$
$$ \begin{align*} \sum_{(\alpha)} \prod_{i=1}^{k} 2^{(b+c) ({\alpha_i}^2/\sqrt{\log \alpha_i}) + (5/6) \log \alpha_i + \log6} s^{(3+c){\alpha_i}^2},\end{align*} $$
where the sum is over all unordered partitions
![]() $\alpha _{1}, \ldots , \alpha _{k}$
of
$\alpha _{1}, \ldots , \alpha _{k}$
of
![]() $\alpha $
. We assume that if
$\alpha $
. We assume that if
![]() $\alpha _i =1$
for some i, then the part of the expression corresponding to it in the product is 1. Since
$\alpha _i =1$
for some i, then the part of the expression corresponding to it in the product is 1. Since
![]() $x/\sqrt {\log x}$
is increasing for
$x/\sqrt {\log x}$
is increasing for
![]() $x> e^{1/2}$
and
$x> e^{1/2}$
and
![]() $\alpha = \alpha _{1} + \cdots + \alpha _{k}$
,
$\alpha = \alpha _{1} + \cdots + \alpha _{k}$
,
 $$ \begin{align*} \prod_{i=1}^{k} 2^{(b+c) ({\alpha_i}^2/\sqrt{\log \alpha_i}) + (5/6) \log \alpha_i + \log6} \leq 2^{(b+c) ({\alpha}^2/\sqrt{\log \alpha}) + (5/6) \alpha \log \alpha + \alpha \log6}. \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{k} 2^{(b+c) ({\alpha_i}^2/\sqrt{\log \alpha_i}) + (5/6) \log \alpha_i + \log6} \leq 2^{(b+c) ({\alpha}^2/\sqrt{\log \alpha}) + (5/6) \alpha \log \alpha + \alpha \log6}. \end{align*} $$
It is not difficult to show that the number of unordered partitions of
![]() $\alpha $
is at most
$\alpha $
is at most
![]() $2^{\alpha -1}$
. So the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
$2^{\alpha -1}$
. So the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
provided
![]() $\alpha> 1$
.
$\alpha> 1$
.
We end this section with the following remark that provides an alternative bound.
Remark 4.3. We do not have an estimate for the constants b and c occurring in Theorem 1.5. If we use a weaker fact that any subgroup of
![]() $S_n$
can be generated by
$S_n$
can be generated by
![]() $\lfloor n/2 \rfloor $
elements for all
$\lfloor n/2 \rfloor $
elements for all
![]() $n \geq 3$
, then we get a weaker result that the number of transitive subgroups of
$n \geq 3$
, then we get a weaker result that the number of transitive subgroups of
![]() $S_n$
that are in
$S_n$
that are in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
![]() $6^{n(n-1)/4} 2^{(n+2) \log n}$
. Using this in the proof of Theorem 1.5 shows that the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
$6^{n(n-1)/4} 2^{(n+2) \log n}$
. Using this in the proof of Theorem 1.5 shows that the number of conjugacy classes of subgroups that are maximal amongst the subgroups of
![]() $\mathrm{GL}(\alpha , s)$
that are also in
$\mathrm{GL}(\alpha , s)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
is at most
$\mathfrak {A}_q\mathfrak {A}_r$
is at most
where
![]() $t, q$
and r are distinct primes, s is a power of t, and
$t, q$
and r are distinct primes, s is a power of t, and
![]() $\alpha \in \mathbb {N}$
.
$\alpha \in \mathbb {N}$
.
5. Enumeration of groups in
 $\mathfrak {A}_p\mathfrak {A}_q \mathfrak {A}_r$
$\mathfrak {A}_p\mathfrak {A}_q \mathfrak {A}_r$
In this section, we prove Theorem 1.2, namely,
where
![]() $n=p^{\alpha }q^{\beta }r^{\gamma }$
and
$n=p^{\alpha }q^{\beta }r^{\gamma }$
and
![]() $\alpha , \beta , \gamma \in \mathbb { N}$
. We use techniques adapted from [Reference Pyber9, Reference Venkataraman13, Reference Venkataraman14].
$\alpha , \beta , \gamma \in \mathbb { N}$
. We use techniques adapted from [Reference Pyber9, Reference Venkataraman13, Reference Venkataraman14].
Proof of Theorem 1.2.
Let G be a group of order
![]() $n = p^{\alpha }q^{\beta }r^{\gamma }$
in
$n = p^{\alpha }q^{\beta }r^{\gamma }$
in
![]() $\mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
. Then
$\mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
. Then
![]() $G= P \rtimes H$
, where P is the unique Sylow p-subgroup of G and
$G= P \rtimes H$
, where P is the unique Sylow p-subgroup of G and
![]() $H \in \mathfrak {A}_q\mathfrak {A}_r$
. So we can write
$H \in \mathfrak {A}_q\mathfrak {A}_r$
. So we can write
![]() $H =Q \rtimes R$
, where
$H =Q \rtimes R$
, where
![]() $|Q|=q^{\beta }$
and
$|Q|=q^{\beta }$
and
![]() $|R|=r^{\gamma }$
. Let
$|R|=r^{\gamma }$
. Let
![]() $G_{1}={G}/{O_{p'}{(G)}}$
,
$G_{1}={G}/{O_{p'}{(G)}}$
,
![]() $G_{2}={G}/{O_{q'}{(G)}}$
and
$G_{2}={G}/{O_{q'}{(G)}}$
and
![]() $G_{3}={G}/{O_{r'}{(G)}}$
. Clearly, each
$G_{3}={G}/{O_{r'}{(G)}}$
. Clearly, each
![]() $G_{i}$
is a soluble A-group and
$G_{i}$
is a soluble A-group and
![]() $G \leq G_{1} \times G_{2} \times G_{3}$
as a subdirect product. Further,
$G \leq G_{1} \times G_{2} \times G_{3}$
as a subdirect product. Further,
![]() ${O_{p'}{(G_{1})}}=1={O_{q'}{(G_{2})}}={O_{r'}{(G_{3})}}$
.
${O_{p'}{(G_{1})}}=1={O_{q'}{(G_{2})}}={O_{r'}{(G_{3})}}$
.
Since
![]() $G_{1}={G}/{O_{p'}{(G)}}$
, we see that
$G_{1}={G}/{O_{p'}{(G)}}$
, we see that
![]() $G_{1} \in \mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
and if
$G_{1} \in \mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
and if
![]() $P_1$
is the Sylow p-subgroup of
$P_1$
is the Sylow p-subgroup of
![]() $G_1$
, then
$G_1$
, then
![]() $P_{1} \cong P$
. Thus,
$P_{1} \cong P$
. Thus,
![]() $|G_1|=p^{\alpha }q^{\beta _{1}}r^{\gamma _{1}}$
and we can write
$|G_1|=p^{\alpha }q^{\beta _{1}}r^{\gamma _{1}}$
and we can write
![]() $G_{1}= P_{1} \rtimes H_{1}$
, where
$G_{1}= P_{1} \rtimes H_{1}$
, where
![]() ${H_{1} \in \mathfrak {A}_q\mathfrak {A}_r}$
. So
${H_{1} \in \mathfrak {A}_q\mathfrak {A}_r}$
. So
![]() $H_{1}= Q_{1} \rtimes R_{1}$
, where
$H_{1}= Q_{1} \rtimes R_{1}$
, where
![]() $Q_{1}\in \mathfrak {A}_q$
and
$Q_{1}\in \mathfrak {A}_q$
and
![]() $|Q_1|=q^{\beta _{1}}$
,
$|Q_1|=q^{\beta _{1}}$
,
![]() $R_{1}\in \mathfrak {A}_r$
and
$R_{1}\in \mathfrak {A}_r$
and
![]() $|R_1|=r^{\gamma _{1}}$
. Further,
$|R_1|=r^{\gamma _{1}}$
. Further,
![]() $H_{1}$
acts faithfully on
$H_{1}$
acts faithfully on
![]() $P_{1}$
. Hence, we can regard
$P_{1}$
. Hence, we can regard
![]() $H_1 \leq \mathrm{Aut}(P_{1}) \cong \mathrm{GL}(\alpha , p)$
. Let
$H_1 \leq \mathrm{Aut}(P_{1}) \cong \mathrm{GL}(\alpha , p)$
. Let
![]() $M_{1}$
be a subgroup that is maximal amongst
$M_{1}$
be a subgroup that is maximal amongst
![]() $p'$
-A-subgroups of
$p'$
-A-subgroups of
![]() $\mathrm{GL}(\alpha , p)$
that are also in
$\mathrm{GL}(\alpha , p)$
that are also in
![]() $\mathfrak {A}_q\mathfrak {A}_r$
and such that
$\mathfrak {A}_q\mathfrak {A}_r$
and such that
![]() $H_{1} \leq M_{1}$
. Let
$H_{1} \leq M_{1}$
. Let
![]() $\hat {G_{1}}=P_{1}M_{1}$
. The number of conjugacy classes of the
$\hat {G_{1}}=P_{1}M_{1}$
. The number of conjugacy classes of the
![]() $M_{1}$
in
$M_{1}$
in
![]() $\mathrm{GL}(\alpha , p)$
is at most
$\mathrm{GL}(\alpha , p)$
is at most
![]() $p^{5\alpha ^{2}} 6^{\alpha (\alpha -1)/4} 2^{\alpha - 1 + (23/6) \alpha \log \alpha + \alpha \log 6}$
by Remark 4.3.
$p^{5\alpha ^{2}} 6^{\alpha (\alpha -1)/4} 2^{\alpha - 1 + (23/6) \alpha \log \alpha + \alpha \log 6}$
by Remark 4.3.
Since
![]() $G_{2}={G}/{O_{q'}{(G)}}$
, we see that
$G_{2}={G}/{O_{q'}{(G)}}$
, we see that
![]() $G_{2} \in \mathfrak {A}_q\mathfrak {A}_r$
and if
$G_{2} \in \mathfrak {A}_q\mathfrak {A}_r$
and if
![]() $Q_2$
is the Sylow q-subgroup of
$Q_2$
is the Sylow q-subgroup of
![]() $G_2$
, then
$G_2$
, then
![]() $Q_{2} \cong Q$
. Thus,
$Q_{2} \cong Q$
. Thus,
![]() $|G_2|=q^{\beta }r^{\gamma _{2}}$
and we can write
$|G_2|=q^{\beta }r^{\gamma _{2}}$
and we can write
![]() $G_{2}=Q_{2} \rtimes H_{2}$
, where
$G_{2}=Q_{2} \rtimes H_{2}$
, where
![]() $H_{2} \in \mathfrak {A}_r$
. So
$H_{2} \in \mathfrak {A}_r$
. So
![]() $|H_2|=r^{\gamma _{2}}$
. Also,
$|H_2|=r^{\gamma _{2}}$
. Also,
![]() $H_2 \leq \mathrm{Aut}(Q_{2}) \cong \mathrm{GL}(\beta , q)$
. Let
$H_2 \leq \mathrm{Aut}(Q_{2}) \cong \mathrm{GL}(\beta , q)$
. Let
![]() $M_{2}$
be a subgroup that is maximal amongst
$M_{2}$
be a subgroup that is maximal amongst
![]() $q'$
-A-subgroups of
$q'$
-A-subgroups of
![]() $\mathrm{GL}(\beta , q)$
that are also in
$\mathrm{GL}(\beta , q)$
that are also in
![]() $\mathfrak {A}_r$
and such that
$\mathfrak {A}_r$
and such that
![]() $H_{2} \leq M_{2}$
. Let
$H_{2} \leq M_{2}$
. Let
![]() $\hat {G_{2}} = Q_{2}M_{2}$
. The number of conjugacy classes of
$\hat {G_{2}} = Q_{2}M_{2}$
. The number of conjugacy classes of
![]() $M_{2}$
in
$M_{2}$
in
![]() $\mathrm{GL}(\beta , q)$
is at most
$\mathrm{GL}(\beta , q)$
is at most
![]() $1$
by Proposition 3.2.
$1$
by Proposition 3.2.
Since
![]() $G_{3}={G}/{O_{r'}{(G)}}$
, we see that
$G_{3}={G}/{O_{r'}{(G)}}$
, we see that
![]() $G_{3} \in \mathfrak {A}_r\mathfrak {A}_q$
and if
$G_{3} \in \mathfrak {A}_r\mathfrak {A}_q$
and if
![]() $R_3$
is the Sylow r-subgroup of
$R_3$
is the Sylow r-subgroup of
![]() $G_3$
, then
$G_3$
, then
![]() $R_{3} \cong R$
. Thus,
$R_{3} \cong R$
. Thus,
![]() $|G_3|=q^{\beta _3}r^{\gamma }$
and we can write
$|G_3|=q^{\beta _3}r^{\gamma }$
and we can write
![]() $G_{3}=R_{3} \rtimes H_{3}$
, where
$G_{3}=R_{3} \rtimes H_{3}$
, where
![]() $H_{3} \in \mathfrak {A}_r$
. So
$H_{3} \in \mathfrak {A}_r$
. So
![]() $|H_3|=q^{\beta _{3}}$
. Also,
$|H_3|=q^{\beta _{3}}$
. Also,
![]() $H_3 \leq \mathrm{Aut}(R_{3}) \cong \mathrm{GL}(\gamma , r)$
. Let
$H_3 \leq \mathrm{Aut}(R_{3}) \cong \mathrm{GL}(\gamma , r)$
. Let
![]() $M_{3}$
be a subgroup that is maximal amongst
$M_{3}$
be a subgroup that is maximal amongst
![]() $r'$
-A-subgroups of
$r'$
-A-subgroups of
![]() $\mathrm{GL}(\gamma , r)$
that are also in
$\mathrm{GL}(\gamma , r)$
that are also in
![]() $\mathfrak {A}_q$
and such that
$\mathfrak {A}_q$
and such that
![]() $H_{3} \leq M_{3}$
. Let
$H_{3} \leq M_{3}$
. Let
![]() $\hat {G_{3}} = R_{3}M_{3}$
. The number of conjugacy classes of the
$\hat {G_{3}} = R_{3}M_{3}$
. The number of conjugacy classes of the
![]() $M_{3}$
in
$M_{3}$
in
![]() $\mathrm{GL}(\gamma , r)$
is at most
$\mathrm{GL}(\gamma , r)$
is at most
![]() $1$
by Proposition 3.2.
$1$
by Proposition 3.2.
Let
![]() $\hat {G} = \hat {G_{1}} \times \hat {G_{2}} \times \hat {G_{3}}$
. Then
$\hat {G} = \hat {G_{1}} \times \hat {G_{2}} \times \hat {G_{3}}$
. Then
![]() $G \leq \hat {G}$
. The choices for
$G \leq \hat {G}$
. The choices for
![]() $P_{1}, Q_{2}$
and
$P_{1}, Q_{2}$
and
![]() $R_{3}$
are unique, up to isomorphism. We enumerate the possibilities for
$R_{3}$
are unique, up to isomorphism. We enumerate the possibilities for
![]() $\hat {G}$
up to isomorphism and then find the number of subgroups of
$\hat {G}$
up to isomorphism and then find the number of subgroups of
![]() $\hat {G}$
of order n up to isomorphism. For the former, we count the number of
$\hat {G}$
of order n up to isomorphism. For the former, we count the number of
![]() $\hat {G_{i}}$
up to isomorphism which depends on the conjugacy class of the
$\hat {G_{i}}$
up to isomorphism which depends on the conjugacy class of the
![]() $M_{i}$
. Hence, the number of choices for
$M_{i}$
. Hence, the number of choices for
![]() $\hat {G}$
up to isomorphism is
$\hat {G}$
up to isomorphism is
![]() $\prod _{i=1}^{3} \{\text {number of choices for } \hat {G_{i}} \text { up to isomorphism}\}$
. Now we estimate the choices for G as a subgroup of
$\prod _{i=1}^{3} \{\text {number of choices for } \hat {G_{i}} \text { up to isomorphism}\}$
. Now we estimate the choices for G as a subgroup of
![]() $\hat {G}$
using a method of ‘Sylow systems’ introduced by Pyber in [Reference Pyber9] .
$\hat {G}$
using a method of ‘Sylow systems’ introduced by Pyber in [Reference Pyber9] .
Let
![]() $\hat {G}$
be fixed. We count the number of choices for G as a subgroup of
$\hat {G}$
be fixed. We count the number of choices for G as a subgroup of
![]() $\hat {G}$
. Let
$\hat {G}$
. Let
![]() ${\cal S} = \{S_{1}, S_{2}, S_{3}\}$
be a Sylow system for G, where
${\cal S} = \{S_{1}, S_{2}, S_{3}\}$
be a Sylow system for G, where
![]() $S_{1}$
is the Sylow p-subgroup of G,
$S_{1}$
is the Sylow p-subgroup of G,
![]() $S_{2}$
is a Sylow q-subgroup of G and
$S_{2}$
is a Sylow q-subgroup of G and
![]() $S_{3}$
is a Sylow r-subgroup of G such that
$S_{3}$
is a Sylow r-subgroup of G such that
![]() $S_{i}S_{j} = S_{j}S_{i}$
for all
$S_{i}S_{j} = S_{j}S_{i}$
for all
![]() $i, j=1,2,3$
. Then
$i, j=1,2,3$
. Then
![]() $G = S_{1} S_{2} S_{3}$
. By [Reference Blackburn, Neumann and Venkataraman1, Theorem 6.2, page 49], there exists
$G = S_{1} S_{2} S_{3}$
. By [Reference Blackburn, Neumann and Venkataraman1, Theorem 6.2, page 49], there exists
![]() ${{\cal B} = \{B_{1}, B_{2}, B_{3}\}}$
, a Sylow system for
${{\cal B} = \{B_{1}, B_{2}, B_{3}\}}$
, a Sylow system for
![]() $\hat {G}$
such that
$\hat {G}$
such that
![]() $S_{i} \leq B_{i}$
, where
$S_{i} \leq B_{i}$
, where
![]() $B_{1}$
is the Sylow p-subgroup of
$B_{1}$
is the Sylow p-subgroup of
![]() $\hat {G}$
,
$\hat {G}$
,
![]() $B_{2}$
is a Sylow q-subgroup of
$B_{2}$
is a Sylow q-subgroup of
![]() $\hat {G}$
and
$\hat {G}$
and
![]() $B_{3}$
is a Sylow r-subgroup of
$B_{3}$
is a Sylow r-subgroup of
![]() $\hat {G}$
. Note that
$\hat {G}$
. Note that
![]() $|B_1|=p^{\alpha }$
. Further, any two Sylow systems for
$|B_1|=p^{\alpha }$
. Further, any two Sylow systems for
![]() $\hat {G}$
are conjugate. Hence, the number of choices for G as a subgroup of
$\hat {G}$
are conjugate. Hence, the number of choices for G as a subgroup of
![]() $\hat {G}$
and up to conjugacy is at most
$\hat {G}$
and up to conjugacy is at most
We observe that
![]() $B_2= T_{21} \times T_{22} \times T_{23}$
, where
$B_2= T_{21} \times T_{22} \times T_{23}$
, where
![]() $T_{2i}$
are Sylow q-subgroups of
$T_{2i}$
are Sylow q-subgroups of
![]() $\hat {G_{i}}$
for
$\hat {G_{i}}$
for
![]() $i=1,2,3$
. From [Reference Venkataraman13, Proposition 3.1],
$i=1,2,3$
. From [Reference Venkataraman13, Proposition 3.1],
![]() $|T_{21}| \leq |M_1| \leq (6^{1/2})^{{\alpha }-1} p^{\alpha }$
and
$|T_{21}| \leq |M_1| \leq (6^{1/2})^{{\alpha }-1} p^{\alpha }$
and
![]() $|T_{23}| = |M_3| \leq (6^{1/2})^{{\gamma }-1} r^{\gamma }$
. Further,
$|T_{23}| = |M_3| \leq (6^{1/2})^{{\gamma }-1} r^{\gamma }$
. Further,
![]() $|T_{22}|=|Q_2|=q^{\beta }$
. Hence,
$|T_{22}|=|Q_2|=q^{\beta }$
. Hence,
![]() $|B_2| \leq (6^{1/2})^{{\alpha + \gamma }-2} p^{\alpha } q^{\beta } r^{\gamma } \leq (6^{1/2})^{{\alpha + \gamma }} n$
and so
$|B_2| \leq (6^{1/2})^{{\alpha + \gamma }-2} p^{\alpha } q^{\beta } r^{\gamma } \leq (6^{1/2})^{{\alpha + \gamma }} n$
and so
![]() $|B_2|^{\beta } \leq (6^{1/2})^{({\alpha + \gamma })\beta } n^{\beta }$
. Similarly, we can show that
$|B_2|^{\beta } \leq (6^{1/2})^{({\alpha + \gamma })\beta } n^{\beta }$
. Similarly, we can show that
![]() $|B_3| \leq (6^{1/2})^{{\alpha + \beta }-2} p^{\alpha } q^{\beta } r^{\gamma }$
. So
$|B_3| \leq (6^{1/2})^{{\alpha + \beta }-2} p^{\alpha } q^{\beta } r^{\gamma }$
. So
![]() $|B_3|^{\gamma } \leq (6^{1/2})^{({\alpha + \beta })\gamma } n^{\gamma }$
. Putting all the estimates together, the number of choices for G as a subgroup of
$|B_3|^{\gamma } \leq (6^{1/2})^{({\alpha + \beta })\gamma } n^{\gamma }$
. Putting all the estimates together, the number of choices for G as a subgroup of
![]() $\hat {G}$
up to conjugacy is at most
$\hat {G}$
up to conjugacy is at most
![]() $|B_1|^{\alpha } |B_2|^{\beta } |B_3|^{\gamma }$
, which is at most
$|B_1|^{\alpha } |B_2|^{\beta } |B_3|^{\gamma }$
, which is at most
Therefore, the number of groups of order
![]() $p^{\alpha }q^{\beta }r^{\gamma }$
in
$p^{\alpha }q^{\beta }r^{\gamma }$
in
![]() $\mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
up to isomorphism is at most
$\mathfrak {A}_p\mathfrak {A}_q\mathfrak {A}_r$
up to isomorphism is at most
 $$ \begin{align*} & p^{5\alpha^{2}} \, 6^{\alpha(\alpha-1)/4} \,2^{\alpha - 1 + (23/6) \alpha \log\alpha + \alpha \log6}\, p^{{\alpha}^2}\, (6^{1/2})^{{({\alpha + \gamma})\beta} + {({\alpha + \beta})\gamma}}\, n^{\beta + \gamma} \\ &\quad= p^{6\alpha^{2}} \,2^{\alpha - 1 + (23/6) \alpha \log\alpha + \alpha \log6} (6^{1/2})^{{({\alpha + \gamma})\beta} + {({\alpha + \beta})\gamma} +{\alpha(\alpha-1)/2}}\, n^{\beta + \gamma}.\\[-36pt] \end{align*} $$
$$ \begin{align*} & p^{5\alpha^{2}} \, 6^{\alpha(\alpha-1)/4} \,2^{\alpha - 1 + (23/6) \alpha \log\alpha + \alpha \log6}\, p^{{\alpha}^2}\, (6^{1/2})^{{({\alpha + \gamma})\beta} + {({\alpha + \beta})\gamma}}\, n^{\beta + \gamma} \\ &\quad= p^{6\alpha^{2}} \,2^{\alpha - 1 + (23/6) \alpha \log\alpha + \alpha \log6} (6^{1/2})^{{({\alpha + \gamma})\beta} + {({\alpha + \beta})\gamma} +{\alpha(\alpha-1)/2}}\, n^{\beta + \gamma}.\\[-36pt] \end{align*} $$