Some results for the Bergman functions in unbounded domains are shown. In particular, a class of unbounded Hartogs domains, which are Bergman complete and Bergman exhaustive, is given.

Let D be a bounded pseudoconvex domain in ℂn and ζ ∈ D. By KD and BD we denote the Bergman kernel and metric of D, respectively. Given a ball B = B(ζ, R), we study the behavior of the ratio KD/KD∩B(w) when w ∈ D ∩ B tends towards ζ. It is well-known, that it remains bounded from above and below by a positive constant. We show, that the ratio tends to 1, as w tends to ζ, under an additional assumption on the pluricomplex Green function 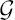D(·, w) of D with pole at w, namely that the diameter of the sublevel sets Aw :={z ∈ D | 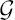D(z, w) < −1} tends to zero, as w → ζ. A similar result is obtained also for the Bergman metric. In this case we also show that the extremal function associated to the Bergman kernel has the concentration of mass property introduced in [DiOh1], where the question was discussed how to recognize a weight function from the associated Bergman space. The hypothesis concerning the set Aw is satisfied for example, if the domain is regular in the sense of Diederich-Fornæss, ([DiFo2]).