Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T21:15:50.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization lemmas for the Bergman metric at plurisubharmonic peak points

Published online by Cambridge University Press:  22 January 2016

Gregor Herbort
Gregor Herbort*
Affiliation:
Fachbereich C - Mathematik und Naturwissenschaften, Bergische Universität Wuppertal, Gaußstraße 20, D-42097 Wuppertal, Germany, gregor@math.uni-wuppertal.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a bounded pseudoconvex domain in ℂn and ζ ∈ D. By KD and BD we denote the Bergman kernel and metric of D, respectively. Given a ball B = B(ζ, R), we study the behavior of the ratio KD/KD∩B(w) when w ∈ D ∩ B tends towards ζ. It is well-known, that it remains bounded from above and below by a positive constant. We show, that the ratio tends to 1, as w tends to ζ, under an additional assumption on the pluricomplex Green function 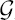D(·, w) of D with pole at w, namely that the diameter of the sublevel sets Aw :={z ∈ D | 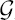D(z, w) < −1} tends to zero, as w → ζ. A similar result is obtained also for the Bergman metric. In this case we also show that the extremal function associated to the Bergman kernel has the concentration of mass property introduced in [DiOh1], where the question was discussed how to recognize a weight function from the associated Bergman space. The hypothesis concerning the set Aw is satisfied for example, if the domain is regular in the sense of Diederich-Fornæss, ([DiFo2]).

Keywords

32A3632F4532U35
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 171 , 2003 , pp. 107 - 125
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2003

References

[BeFo] Bedford, E. and Fornæss, J.E., Biholomorphic maps of weakly pseudoconvex domains, Duke Math. J., 45 (1978), 711–719.CrossRefGoogle Scholar
[Blo] Błocki, Z., Estimates for the complex Monge-Ampére operator, Bull. Pol. Acad. Sci., 41 (1993), 151–157.Google Scholar
[BlPf] Błocki, Z. and Pflug, P., Hyperconvexity and Bergman completeness, Nagoya Math. J., 151 (1998), 221–225.CrossRefGoogle Scholar
[CCW] Carlehed, M., Cegrell, U. and Wikström, F., Jensen measures, Hyperconvexity and Boundary Behavior of the Pluricomplex Green’s Function, Ann. Pol. Math., 71 (1999), 87–103.CrossRefGoogle Scholar
[Di] Diederich, K., Randverhalten der Bergmanschen Kernfunktion und Metrik in streng pseudokonvexen Gebieten, Math. Ann., 198 (1970), 1–36.Google Scholar
[DiFo1] Diederich, K. and Fornæss, J.E., Pseudoconvex domains: Bounded strictly plurisubharmonic exhaustion functions, Inv. Math., 39 (1977), 129–141.CrossRefGoogle Scholar
[DiFo2] Diederich, K. and Fornæss, J.E., Pseudoconvex domains: Existence of Stein neighborhoods, Duke Math. J., 44 (1977), 641–662.CrossRefGoogle Scholar
[DiFoHe] Diederich, K., Fornæss, J.E. and Herbort, G., Boundary behavior of the Bergman metric, Proc. Pure Math., 41 (1984), 59–67.Google Scholar
[DiHe1] Diederich, K. and Herbort, G., Pseudoconvex domains of semiregular type, Contributions to Complex Analysis and Analytic Geometry (Skoda,H.-Trépreau, Eds.), Aspects of Mathematics, E26 (1994), 127–162.Google Scholar
[DiHe2] Diederich, K. and Herbort, G., Quantitative estimates for the Green function and an application to the Bergman metric, Ann. Inst. Fourier (Grenoble), 50 (2000), 1205–1228.CrossRefGoogle Scholar
[DiHe3] Diederich, K. and Herbort, G., An alternative proof of a theorem of T. Ohsawa, Michigan Mathematics J., 46 (1999), 347–360.CrossRefGoogle Scholar
[DiOh1] Diederich, K. and Ohsawa, T., Moment problems for weighted Bergman kernels, Complex analysis and geometry (Paris, 1997), Progress in Mathematics, 188 (2000), 111–122.CrossRefGoogle Scholar
[DiOh2] Diederich, K. and Herbort, G., An estimate for the Bergman distance on pseudoconvex domains, Ann. of Math., 141 (1995), 181–190.CrossRefGoogle Scholar
[De] Demailly, J.-P., Mesures de Monge-Ampére et mesures pluriharmoniques, Math. Z., 194 (1987), 519–564.CrossRefGoogle Scholar
[FoSi] Fornæss, J.E. and Sibony, N., Construction of p.s.h. functions on weakly pseudoconvex domains, Duke Math. J., 58 (1989), 633–656.CrossRefGoogle Scholar
[He1] Herbort, G., The Bergman metric on hyperconvex domains, Math. Z., 232 (1999), 183–196.CrossRefGoogle Scholar
[He2] Herbort, G., Boundary behavior of the pluricomplex Green function on pseudoconvex domains with a smooth boundary, Internatl. J. Math., 11 (2000), 509–522.CrossRefGoogle Scholar
[Hoer] Hörmander, L., L2-estimates and existence theorems for the ∂̅-operator, Acta Math., 113 (1965), 89–152.CrossRefGoogle Scholar
[Kli] Klimek, M., Extremal plurisubharmonic functions and invariant pseudodistances, Bull. Soc. Math. France, 113 (1985), 231–240.CrossRefGoogle Scholar
[KrYu] Krantz, S. and Yu, J., On the Bergman invariant and curvatures of the Bergman metric, Illinois J. Math., 40 (1996), 226–244.CrossRefGoogle Scholar
[McN] McNeal, J., Lower bounds on the Bergman metric near a point of finite type, Ann. Math., 136 (1992), 339–360.CrossRefGoogle Scholar
[Nik] Nikolov, N., Localization of invariant metrics, Arch. Math., 79 (2002), 67–73.CrossRefGoogle Scholar
[Oh1] Ohsawa, T., Boundary behavior of the Bergman kernel function on pseudoconvex domains, Publ. R.I.M.S. Kyoto University, 20 (1984), 897–902.CrossRefGoogle Scholar
[OhTa] Ohsawa, T. and Takegoshi, K., On the extension of L2-holomorphic functions, Math. Z., 195 (1987), 197–204.CrossRefGoogle Scholar
[Si] Sibony, N., Une classe de domaines pseudoconvexes, Duke Math. J., 55 (1987), 299–319.CrossRefGoogle Scholar
[Yu] Yu, J., Peak functions on weakly pseudoconvex domains, Indiana Univ. Math. J., 43 (1994), 1271–1295.CrossRefGoogle Scholar