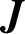 $\boldsymbol {J}$
-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
$\boldsymbol {J}$
-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
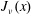 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}J_\nu (x)$ in the transition region
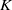 $K$-Bessel function of imaginary order
$K$-Bessel function of imaginary order