Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T04:56:15.940Z Has data issue: false hasContentIssue false
  • English
  • Français

ON AN INTEGRAL OF $\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE

Part of: Stochastic processes

Published online by Cambridge University Press:  09 July 2021

GEORGE ANTON Open the ORCID record for GEORGE ANTON [Opens in a new window] ,
JESSEN A. MALATHU Open the ORCID record for JESSEN A. MALATHU [Opens in a new window] ,
SHELBY STINSON Open the ORCID record for SHELBY STINSON [Opens in a new window]  and
J. S. Friedman
GEORGE ANTON
Affiliation:
Department of Mathematics, The City College of New York, Convent Avenue at 138th Street, New York, NY10031, USA e-mail: ganton000@citymail.cuny.edu, SendittoGeorgeAnton@gmail.com
JESSEN A. MALATHU*
Affiliation:
Department of Mathematics, The City College of New York, Convent Avenue at 138th Street, New York, NY10031, USA
SHELBY STINSON
Affiliation:
Department of Mathematics, Fordham University, 441 E. Fordham Road, Bronx, NY 10458, USA e-mail: sstinson1@fordham.edu, shstinson96@gmail.com
J. S. Friedman*
Affiliation:
Department of Mathematics and Science, United States Merchant Marine Academy, 300 Steamboat Road, Kings Point, NY 11024, USA e-mail: FriedmanJ@usmma.edu, joshua@math.sunysb.edu, CrownEagle@gmail.com
*
e-mail: jmalath000@citymail.cuny.edu, jmalathu@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Cogdell et al. [‘Evaluating the Mahler measure of linear forms via Kronecker limit formulas on complex projective space’, Trans. Amer. Math. Soc. (2021), to appear] developed infinite series representations for the logarithmic Mahler measure of a complex linear form with four or more variables. We establish the case of three variables by bounding an integral with integrand involving the random walk probability density 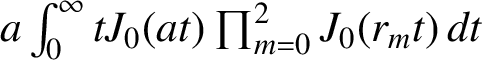$a\int _0^\infty tJ_0(at) \prod _{m=0}^2 J_0(r_m t)\,dt$ , where 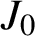$J_0$ is the order-zero Bessel function of the first kind and a and 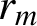$r_m$ are positive real numbers. To facilitate our proof we develop an alternative description of the integral’s asymptotic behaviour at its known points of divergence. As a computational aid for numerical experiments, an algorithm to calculate these series is presented in the appendix.

Keywords

Mahler measurerandom walkBessel function

MSC classification

Secondary: 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$ 60G50: Sums of independent random variables; random walks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 2 , April 2022 , pp. 223 - 235
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors acknowledge the support of NSF grant DMS-1820731.

†

The views expressed in this article are the author’s own and not those of the United States Merchant Marine Academy, the Maritime Administration, the Department of Transportation or the United States government.

References

Bailey, D. H. and Borwein, J. M., ‘Hand-to-hand combat with thousand-digit integrals’, J. Comput. Sci. 3(3) (2012), 77–86.10.1016/j.jocs.2010.12.004CrossRefGoogle Scholar
Balasubramanian, R. and Ponnusamy, S., ‘On Ramanujan asymptotic expansions and inequalities for hypergeometric functions’, Proc. Indian Acad. Sci. Math. Sci. 108 (1998), 95–108.10.1007/BF02841543CrossRefGoogle Scholar
Borwein, J. M. and Straub, A., ‘Mahler measures, short walks and log-sine integrals’, Theoret. Comput. Sci. 479(1) (2013), 4–21.10.1016/j.tcs.2012.10.025CrossRefGoogle Scholar
Borwein, J. M., Straub, A., Wan, J. and Zudilin, W., ‘Densities of short uniform random walks (with an appendix by D. Zagier)’, Canad. J. Math. 5(64) (2012), 961–990.10.4153/CJM-2011-079-2CrossRefGoogle Scholar
Cogdell, J., Jorgenson, J. and Smajlović, L., ‘Evaluating the Mahler measure of linear forms via Kronecker limit formulas on complex projective space’, Trans. Amer. Math. Soc. (2021), to appear.10.1090/tran/8432CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series and Products, 7th edn (Academic Press, Amsterdam, 2007).Google Scholar
Harrison, J., ‘Fast and accurate Bessel function computation’, Proc. 19th IEEE Sympos. Computer Arithmetic, Portland, OR (IEEE Computer Society, Washington, DC, 2009), 104–113.10.1109/ARITH.2009.32CrossRefGoogle Scholar
Kluyver, J. C., ‘A local probability problem’, Proc. Sect. Sci. Koninklijke Academie van Weteschappen te Amsterdam 8 (1906), 341–351.Google Scholar
Lalín, M., ‘Mahler measure and elliptic curve L-functions at $s=3$ ’, J. reine angew. Math. 709 (2015), 201–218.Google Scholar
Lang, S., Complex Analysis, 4th edn (Springer, New York, 2005).Google Scholar
Pearson, K., A Mathematical Theory of Random Migration (Dulau, London, 1906).CrossRefGoogle Scholar
Rodriguez-Villegas, F., Toledano, R. and Vaaler, J., ‘Estimates for Mahler’s measure of a linear form’, Proc. Edinb. Math. Soc. 47(10) (2004), 891–921.10.1017/S0013091503000701CrossRefGoogle Scholar
Smyth, C., ‘The Mahler measure of algebraic numbers: a survey’, in: Number Theory and Polynomials, London Mathematical Society Lecture Note Series, 352 (Cambridge University Press, Cambridge, 2008), 322–349.10.1017/CBO9780511721274.021CrossRefGoogle Scholar
Szegö, G., Orthogonal Polynomials (American Mathematical Society, Providence, RI, 1939).Google Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions (Cambridge University Press, Cambridge, 1944).Google Scholar
Zagier, D., ‘The dilogarithm function’, in: Frontiers in Number Theory, Physics, and Geometry II (Springer, Berlin--Heidelberg, 2007), 3–65.Google Scholar