For bounded domains Ω, we prove that the Lp-norm of a regular function with compact support is controlled by weighted Lp-norms of its gradient, where the weight belongs to a class of symmetric non-negative definite matrix-valued functions. The class of weights is defined by regularity assumptions and structural conditions on the degeneracy set, where the determinant vanishes. In particular, the weight A is assumed to have rank at least 1 when restricted to the normal bundle of the degeneracy set S. This generalization of the classical Poincaré inequality is then applied to develop a robust theory of first-order Lp-based Sobolev spaces with matrix-valued weight A. The Poincaré inequality and these Sobolev spaces are then applied to produce various results on existence, uniqueness and qualitative properties of weak solutions to boundary-value problems for degenerate elliptic, degenerate parabolic and degenerate hyperbolic partial differential equations (PDEs) of second order written in divergence form, where A is calibrated to the matrix of coefficients of the second-order spatial derivatives. The notion of weak solution is variational: the spatial states belong to the matrix-weighted Sobolev spaces with p = 2. For the degenerate elliptic PDEs, the Dirichlet problem is treated by the use of the Poincaré inequality and Lax–Milgram theorem, while the treatment of the Cauchy–Dirichlet problem for the degenerate evolution equations relies only on the Poincaré inequality and the parabolic and hyperbolic counterparts of the Lax–Milgram theorem.

The paper deals with blow-up for the solutions of an evolution problem consisting in a semilinear wave equation posed in a bounded C1,1 open subset of ℝn, supplied with a Neumann boundary condition involving a nonlinear dissipation. The typical problem studied is

where ∂Ω = Γ0 ∪ Γ1, Γ0 ∩ Γ1 = ∅, σ(Γ0) > 0, 2 < p ≤ 2(n − 1)/(n − 2) (when n ≥ 3), m > 1, α ∈ L∞(Γ1), α ≥ 0 and β ≥ 0. The initial data are posed in the energy space.The aim of the paper is to improve previous blow-up results concerning the problem.

We estimate the density of resonances close to a critical curve, for strictly convex obstacles with analytic boundary. Contrary to the C∞-case, already treated with Zworski, the estimates are in terms of dynamical quantities. A new feature in the proof is a certain averaging procedure.

A method will be introduced to solve problems utt — uss = h(s, t), u(t,t) - u(1+t,1 - t), u(s,0) = g(s), u(1,1) = 0 and 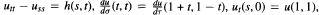for (s, t) in the characteristic triangle R = {(s,t) : t ≤ s ≤ 2 — t, 0 ≤ t ≤ 1}. Here 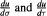represent the directional derivatives of u in the characteristic directions e1 = (— 1, — 1) and e2 = (1, — 1), respectively. The method produces the symmetric Green's function of Kreith [1] in both cases.

Generalized boundary value problems are considered for hyperbolic equations of the form utt — uss + λp(s, t)u = 0. By constructing symmetric Green's functions appropriate to such problems the existence of eigenvalues is established.