There has been renewed interest in Barton and Lord’s (An upper asymptote for the three-parameter logistic item response model (Tech. Rep. No. 80-20). Educational Testing Service, 1981) four-parameter item response model. This paper presents a Bayesian formulation that extends Béguin and Glas (MCMC estimation and some model fit analysis of multidimensional IRT models. Psychometrika, 66 (4):541–561, 2001) and proposes a model for the four-parameter normal ogive (4PNO) model. Monte Carlo evidence is presented concerning the accuracy of parameter recovery. The simulation results support the use of less informative uniform priors for the lower and upper asymptotes, which is an advantage to prior research. Monte Carlo results provide some support for using the deviance information criterion and \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\chi ^{2}$$\end{document}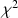 index to choose among models with two, three, and four parameters. The 4PNO is applied to 7491 adolescents’ responses to a bullying scale collected under the 2005–2006 Health Behavior in School-Aged Children study. The results support the value of the 4PNO to estimate lower and upper asymptotes in large-scale surveys.
index to choose among models with two, three, and four parameters. The 4PNO is applied to 7491 adolescents’ responses to a bullying scale collected under the 2005–2006 Health Behavior in School-Aged Children study. The results support the value of the 4PNO to estimate lower and upper asymptotes in large-scale surveys.