Hostname: page-component-5f745c7db-nc56l Total loading time: 0 Render date: 2025-01-06T07:31:59.696Z Has data issue: true hasContentIssue false
  • English
  • Français

Revisiting the 4-Parameter Item Response Model: Bayesian Estimation and Application

Published online by Cambridge University Press:  01 January 2025

Steven Andrew Culpepper
Steven Andrew Culpepper*
Affiliation:
University of Illinois at Urbana-Champaign
*
Correspondence should be made to Steven Andrew Culpepper, Department of Statistics, University of Illinois at Urbana-Champaign, 725 South Wright Street, Champaign, IL 61820, USA. Email: sculpepp@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

There has been renewed interest in Barton and Lord’s (An upper asymptote for the three-parameter logistic item response model (Tech. Rep. No. 80-20). Educational Testing Service, 1981) four-parameter item response model. This paper presents a Bayesian formulation that extends Béguin and Glas (MCMC estimation and some model fit analysis of multidimensional IRT models. Psychometrika, 66 (4):541–561, 2001) and proposes a model for the four-parameter normal ogive (4PNO) model. Monte Carlo evidence is presented concerning the accuracy of parameter recovery. The simulation results support the use of less informative uniform priors for the lower and upper asymptotes, which is an advantage to prior research. 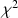Monte Carlo results provide some support for using the deviance information criterion and χ2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\chi ^{2}$$\end{document} index to choose among models with two, three, and four parameters. The 4PNO is applied to 7491 adolescents’ responses to a bullying scale collected under the 2005–2006 Health Behavior in School-Aged Children study. The results support the value of the 4PNO to estimate lower and upper asymptotes in large-scale surveys.

Keywords

4-parameter item response modelBayesianGibbs samplinglarge-scale assessmentbullyingpsychopathology
Type
Article
Information
Psychometrika , Volume 81 , Issue 4 , December 2016 , pp. 1142 - 1163
Copyright
Copyright © 2015 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albert, J. (1992). Bayesian estimation of normal ogive item response curves using Gibbs sampling. Journal of Educational and Behavioral Statistics, 17 (3), 251–269.CrossRefGoogle Scholar
Barton, M A., & Lord, F.M. (1981). An upper asymptote for the three-parameter logistic item-response model (Tech. Rep. No. No. 80-20). Educational Testing Service.Google Scholar
Béguin, A. A., Glas, C. A. (2001). MCMC estimation and some model-fit analysis of multidimensional IRT models. Psychometrika, 66 (4), 541–561.CrossRefGoogle Scholar
Brooks, S. P., Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7 (4), 434–455.CrossRefGoogle Scholar
Chang, H.- H., Ying, Z. (2008). To weight or not to weight? Balancing influence of initial items in adaptive testing. Psychometrika, 73 (3), 441–450.CrossRefGoogle Scholar
Culpepper, S. A. (2015). An improved correction for range restricted correlations under extreme, monotonic quadratic nonlinearity and heteroscedasticity. Psychometrika,Google ScholarPubMed
Feuerstahler, L. M., Waller, N. G. (2014). (2010). Estimation of the 4-parameter model with marginal maximum likelihood. Multivariate Behavioral Research, 49 (3), 285–285.CrossRefGoogle ScholarPubMed
Fox, J.- P. Bayesian item response modeling, New York: Springer.CrossRefGoogle Scholar
Gelman, A., Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science, 7, 457–472.CrossRefGoogle Scholar
Green, B. F. (2011). A comment on early student blunders on computer-based adaptive tests. Applied Psychological Measurement, 35 (2), 165–174.CrossRefGoogle Scholar
Holmes, D. (1990). (2005). The robustness of the usual correction for restriction in range due to explicit selection. Psychometrika, 55, 19–32.CrossRefGoogle Scholar
Iannotti, R. Health behavior in school-aged children HBSC, 2005–2006, Ann Arbor, MI: Inter-university Consortium for Political and Social Research.Google Scholar
Liao, W., Ho, R., Yen, Y., Cheng, H. (2012). The four-parameter logistic item response theory model as a robust method of estimating ability despite aberrant responses. Social Behavior and Personality: An International Journal, 40, 1679–1694.CrossRefGoogle Scholar
Loken, E., Rulison, K. L. (2010). Estimation of a four-parameter item response theory model. British Journal of Mathematical and Statistical Psychology, 63 (3), 509–525.CrossRefGoogle ScholarPubMed
Magis, D. (2013). A note on the item information function of the four-parameter logistic model. Applied Psychological Measurement, 37 (4), 304–315.CrossRefGoogle Scholar
Mendoza, J. (1993). Fisher transformations for correlations corrected for selection and missing data. Psychometrika, 58 (4), 601–615.CrossRefGoogle Scholar
Ogasawara, H. (2012). Asymptotic expansions for the ability estimator in item response theory. Computational Statistics, 27 (4), 661–683.CrossRefGoogle Scholar
Patz, R. J., Junker, B. W. (1999). Applications and extensions of MCMC in IRT: Multiple item types, missing data, and rated responses. Journal of Educational and Behavioral Statistics, 24 (4), 342–366.CrossRefGoogle Scholar
Patz, R. J., Junker, B. W. (1999). A straightforward approach to Markov Chain Monte Carlo methods for item response models. Journal of Educational and Behavioral Statistics, 24 (2), 146–178.CrossRefGoogle Scholar
Pham-Gia, T., Turkkan, N. (1998). Distribution of the linear combination of two general Beta variables and applications. Communications in Statistics Theory and Methods, 27 (7), 1851–1869.CrossRefGoogle Scholar
Reise, S. P., Waller, N. G. (2003). How many IRT parameters does it take to model psychopathology items?. Psychological Methods, 8 (2), 164–184.CrossRefGoogle ScholarPubMed
Rulison, K. L., Loken, E. (2009). I’ve fallen and I can’t get up: Can high-ability students recover from early mistakes in CAT?. Applied Psychological Measurement, 33 (2), 83–101.CrossRefGoogle ScholarPubMed
Sahu, S. K. (2002). Bayesian estimation and model choice in item response models. Journal of Statistical Computation and Simulation, 72 (3), 217–232.CrossRefGoogle Scholar
San Martín, E., González, J., Tuerlinckx, F. (2014). On the unidentifiability of the fixed-effects 3PL model. Psychometrika, 80, 1–18.Google ScholarPubMed
Sinharay, S., Johnson, M. S., Stern, H. S. (2006). Posterior predictive assessment of item response theory models. Applied Psychological Measurement, 30 (4), 298–321.CrossRefGoogle Scholar
Spiegelhalter, D. J., Best, N. G., Carlin, B. P., Van Der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64 (4), 583–639.CrossRefGoogle Scholar
Waller, N. G., Reise, S. P., Embretson, S. (2010). Measuring psychopathology with nonstandard item response theory models: Fitting the four-parameter model to the Minnesota Multiphasic Personality Inventory. Measuring psychological constructs: Advances in model based approaches, Washington, DC: American Psychological Association.Google Scholar
Zheng, Y., Chang, H.- H. (2014). On-the-fly assembled multistage adaptive testing. Applied Psychological Measurement, 39, 104–118.CrossRefGoogle ScholarPubMed