We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let ψ be a non-decreasing continuous subadditive function defined on [0, ∞) and satisfy ψ(x) = 0 if and only if x = 0. The space H(ψ) is defined as the set of analytic functions in the unit disk which satisfy
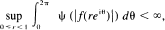
and the space H+ (ψ) is the space of a f ∊ H(ψ) for which
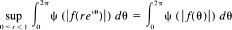
where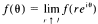 
almost everywhere.
In this paper we study the H(ψ) spaces and characterize the continuous linear functionals on H+ (ψ).
