Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hasumi, Morisuke
and
Kataoka, Sabur�
1988.
Remarks on Hardy-Orlicz classes.
Archiv der Mathematik,
Vol. 51,
Issue. 5,
p.
455.
Matsugu, Yasuo
1992.
On a conjecture of Z. Jianzhong.
Bulletin of the Australian Mathematical Society,
Vol. 45,
Issue. 1,
p.
163.
Lu, Qun
Cao, Guang Fu
and
Liu, Li Fang
2005.
Hardy–Orlicz Spaces and Their Multiplication Operators.
Acta Mathematica Sinica, English Series,
Vol. 21,
Issue. 3,
p.
593.
Masri, Mahmud
2007.
Multiplicative linear functionals and ring homomorphisms of.
Journal of Interdisciplinary Mathematics,
Vol. 10,
Issue. 2,
p.
221.
Xueying Zhang
and
Chuanzhou Zhang
2011.
Weak Orlicz spaces generated by concave functions.
p.
42.
Koskela, Pekka
and
Benedict, Sita
2015.
Intrinsic Hardy-Orlicz spaces of conformal mappings.
Bulletin of the London Mathematical Society,
Vol. 47,
Issue. 1,
p.
75.
Sharma, Ajay K.
Bhat, Ambika
and
Devi, Manisha
2018.
Hardy–Stein Type Identities and Rate of Growth of Mean Values of Functions in Generalized Hardy Spaces.
Complex Analysis and Operator Theory,
Vol. 12,
Issue. 6,
p.
1443.

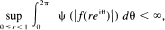
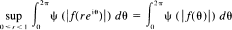
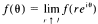 almost everywhere.
almost everywhere.