On a compact connected group $G$, consider the infinitesimal generator $-L$ of a central symmetric Gaussian convolution semigroup ${{\left( {{\mu }_{t}} \right)}_{t>0}}$. Using appropriate notions of distribution and smooth function spaces, we prove that $L$ is hypoelliptic if and only if ${{\left( {{\mu }_{t}} \right)}_{t>0}}$ is absolutely continuous with respect to Haar measure and admits a continuous density $x\mapsto {{\mu }_{t}}\left( x \right),t>0$, such that ${{\lim }_{t\to 0}}t\log {{\mu }_{t}}\left( e \right)=0$. In particular, this condition holds if and only if any Borel measure $u$ which is solution of $Lu=0$ in an open set $\Omega $ can be represented by a continuous function in $\Omega $. Examples are discussed.

Let E′ be the dual of a nuclear Fréchet space E and L*(t) the adjoint operator of a diffusion operator L(t) of infinitely many variables, which has a formal expression:

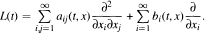
A weak form of the stochastic differential equation

dX(t) = dW(t) + L*(t)X(t)dt

is introduced and the existence of a unique solution is established. The solution process is a random linear functional (in the sense of I. E. Segal) on a space of generalized functionals on E′. The above is an appropriate model for the central limit theorem for an interacting system of spatially extended neurons. Applications to the latter problem are discussed.