Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T05:31:07.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Hypoelliptic Bi-Invariant Laplacians on Infinite Dimensional Compact Groups

Published online by Cambridge University Press:  20 November 2018

A. Bendikov  and
L. Saloff-Coste
A. Bendikov
Affiliation:
Instytut Matematyczny, UniwersytetuWrocławskiego, Poland e-mail: bendikov@math.uni.wroc.pl
L. Saloff-Coste
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853-4201 U.S.A. e-mail: lsc@math.cornell.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On a compact connected group 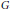$G$, consider the infinitesimal generator 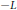$-L$ of a central symmetric Gaussian convolution semigroup 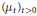${{\left( {{\mu }_{t}} \right)}_{t>0}}$. Using appropriate notions of distribution and smooth function spaces, we prove that 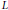$L$ is hypoelliptic if and only if 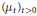${{\left( {{\mu }_{t}} \right)}_{t>0}}$ is absolutely continuous with respect to Haar measure and admits a continuous density 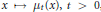$x\mapsto {{\mu }_{t}}\left( x \right),t>0$, such that 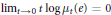${{\lim }_{t\to 0}}t\log {{\mu }_{t}}\left( e \right)=0$. In particular, this condition holds if and only if any Borel measure $u$ which is solution of 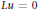$Lu=0$ in an open set 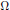$\Omega $ can be represented by a continuous function in 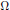$\Omega $. Examples are discussed.

Keywords

60B1543A7735H1046F2560J4560J6
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 4 , 01 August 2006 , pp. 691 - 725
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Bakry, D. Transformation de Riesz pour les semigroupes symétriques. I. Étude de la dimension 1. Séminaire de Probabilités XIX, Lecture Notes in Mathematics 1123, Springer, Berlin, 1985, pp. 130–174.Google Scholar
[2] Bendikov, A. Spatially homogeneous continuous Markov processes on abelian groups and harmonic structures. (Russian) Uspehi Mat. Nauk 29(1974), no. 5, 215–216.Google Scholar
[3] Bendikov, A. Potential Theory on Infinite-Dimensional Abelian Groups. Walter De Gruyter, Berlin, 1995.Google Scholar
[4] Bendikov, A. Symmetric stable semigroups on the infinite dimensional torus. Expo. Math. 13(1995), 39–79.Google Scholar
[5] Bendikov, A. A. and Saloff-Coste, L., Elliptic diffusions on infinite products. J. Reine Angew. Math. 493(1997), 171–220.Google Scholar
[6] Bendikov, A. A. and Saloff-Coste, L., Potential theory on infinite products and locally compact groups. Potential Anal. 11(1999), no. 4, 325–358.Google Scholar
[7] Bendikov, A. A. and Saloff-Coste, L., On- and off-diagonal heat kernel behaviors on certain infinite dimensional local Dirichlet spaces. Amer. J. Math. 122(2000), no. 6, 1205–1263.Google Scholar
[8] Bendikov, A. A. and Saloff-Coste, L., Central Gaussian semigroups of measures with continuous density. J. Funct. Anal. 186(2001), no. 1, 206–268.Google Scholar
[9] Bendikov, A. A. and Saloff-Coste, L., On the absolute continuity of Gaussian measures on locally compact groups. J. Theoret. Probab. 14(2001), no. 3, 887–898.Google Scholar
[10] Bendikov, A. A. and Saloff-Coste, L., Gaussian bounds for derivatives of central Gaussian semigroups on compact groups. Trans. Amer. Math. Soc. 354(2001), no. 4, 1279–1298.Google Scholar
[11] Bendikov, A. A. and Saloff-Coste, L., Invariant local Dirichlet forms on locally compact groups. Ann. Fac. Sci. Toulouse Math. 11(2002), no. 3, 303–349.Google Scholar
[12] Bendikov, A. A. and Saloff-Coste, L., On the hypoellipticity of sub-Laplacians on infinite dimensional compact groups. Forum Math. 15(2003), no. 1, 135–163.Google Scholar
[13] Bendikov, A. A. and Saloff-Coste, L., Brownian motions on compact groups of infinite dimension. In: Heat Kernels and Analysis onManifolds, Graphs, and Metric Spaces. Contemp. Math. 338, American Mathematical Society, Providence, RI, 2003, pp. 41–63.Google Scholar
[14] Bendikov, A. A. and Saloff-Coste, L., Central Gaussian convolution semigroups on compact groups: a survey. Infin. Dimens. Anal. Quantum Probab. Rel. Top. 6(2003), 629–659.Google Scholar
[15] Bendikov, A. A. and Saloff-Coste, L., Spaces of smooth functions and distributions on infinite dimensional compact groups. J. Funct. Anal. 218(2005), 168–218.Google Scholar
[16] Berg, C., Potential theory on the infinite dimensional torus. Invent. Math. 32(1976), no. 1, 49–100.Google Scholar
[17] Bony, J. M., Opérateurs elliptiques dégénérés associés aux axiomatiques de la théorie du potentiel. In: Potential Theory. Edizioni Cremonese, Rome, 1970, pp. 69–119.Google Scholar
[18] Born, É., Projective Lie algebra bases of a locally compact group and uniform differentiability. Math. Z. 200(1989), no. 2, 279–292.Google Scholar
[19] Born, É., An Explicit Lévy-Hinčin formula for convolution semigroups on locally compact groups. J. Theoret. Probab. 2(1989), no. 3, 325–342.Google Scholar
[20] Bourbaki, N., Espaces vectoriels topologiques. In: lments de mathmatique. Ch 1–5, Masson, Paris, 1981.Google Scholar
[21] Bruhat, F., Distributions sur un groupe localement compact et application à l’étude des représentations des groupes p-adiques. Bull. Soc. Math. France 89(1961), 43–75.Google Scholar
[22] Davies, E. B., Heat kernels and spectral theory. Cambridge Tracts in Mathematics 92, Cambridge, Cambridge University Press, 1989.Google Scholar
[23] Davies, E. B., Non-Gaussian aspects of heat kernel behaviour. J. London Math. Soc. 55(1997), no. 1, 105–125.Google Scholar
[24] Fukushima, M., Ōshima, Y., and Takeda, M., Dirichlet forms and Symmetric Markov processes, de Gruyter Studies in Mathematics 19, W. De Gruyter, Berlin, 1994.Google Scholar
[25] Glushkov, V. N., The structure of locally compact groups and Hilbert's Fifth Problem. AMS Translations 15, 1960, 55–94.Google Scholar
[26] Heyer, H., Probability Measures on Locally Compact Groups. Ergebnisse der Mathematik und ihrer Grenzgebieter 94, Springer-Verlag, Berlin, 1977.Google Scholar
[27] Hofmann, K. and Morris, S., The structure of compact groups. A primer for the student—a handbook for the expert. de Gruyter Studies in Mathematics 25. W. de Gruyter, Berlin, 1998.Google Scholar
[28] Hörmander, L., Hypoelliptic second order differential equations. Acta Math. 119(1967), 147–171.Google Scholar
[29] Hunt, G. A., Semi-groups of measures on Lie groups. Trans. Amer. Math. Soc. 81(1956), 264–293.Google Scholar
[30] Kusuoka, S. and Stroock, D., Applications of the Malliavin calculus, Part II. J. Fac. Sci., Univ. Tokyo Sect. IA Math. 32(1985), no. 1, 1–76.Google Scholar
[31] Ledoux, M., L’algèbre de Lie des gradients itérés d’un générateur Markovien—développements de moyennes et entropies. Ann. Sci. École Norm. Sup. (4) 28(1995), no. 4, 435–460.Google Scholar
[32] Siebert, E., Absolute continuity, singularity and supports of Gaussian semigroups on a Lie group. Monats.Math. 93(1982), no. 3, 239–253.Google Scholar
[33] Sturm, K.-T., On the geometry defined by Dirichlet forms. In: Seminar on Stochastic Processes, Random Fields and Applications, Progr. Probab. 36, Birkhäuser, Basel, 1995, pp. 231–242.Google Scholar
[34] Varadarajan, V. S., Lie Groups, Lie Algebras, and Their Representations. Graduate Texts in Mathematics 102, Springer-Verlag, New York, 1984.Google Scholar
[35] Varopoulos, N., Saloff-Coste, L. and Coulhon, T., Analysis and geometry on groups. Cambridge Tracts in Mathematics 100, Cambridge, Cambridge University Press, 1993.Google Scholar