 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
 $\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
$\mathrm{C}^{*}$-algebras hereditarily containing nonzero, square-zero elements
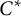 $C^*\!$-algebras
$C^*\!$-algebras
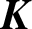 $\boldsymbol {K}$-STABILITY OF CONTINUOUS
$\boldsymbol {K}$-STABILITY OF CONTINUOUS 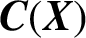 $\boldsymbol {C(X)}$-ALGEBRAS
$\boldsymbol {C(X)}$-ALGEBRAS