1 Introduction
1.1 Background
A cornerstone of groupoid C*-algebra theory is the Kumjian– Renault Weyl groupoid representation. Specifically, given a C*-algebra A with a Cartan subalgebra C, they showed how to construct a Fell line bundle over an étale groupoid on which to represent A as continuous sections, thus realising the abstract algebra A as a concrete twisted groupoid C*-algebra.
One key aspect of their construction is the use of normalisers of C to construct an appropriate groupoid of germs. Recently it has become apparent that this normaliser semigroup S already contains a significant amount of structural information. For example, if A is already known to be a groupoid C*-algebra then this groupoid can be recovered just from the semigroup structure of S and C (as the groupoid of ultrafilters with respect to the ‘domination relation’ on S; see [Reference Bice and Clark4]).
This begs the question whether one can similarly represent a given abstract semigroup S, together with some additional structure coming from appropriate subsemigroups, as a semigroup of sections of some groupoid bundle. This is borne out in the present paper, where we construct universal representations of S on groupoid bundles formed from cosets and filters of S. The basic idea is to extend the relevant theory of inverse semigroups, replacing the idempotents with normal subsemigroups analogous to Cartan subalgebras.
1.2 Outline
As a gentle introduction to our more general results, in Section 2 we first consider simpler classes of semigroups. We start with semilattices and their filters in Section 2.1, moving on to inverse semigroups and their cosets in Section 2.2. Finally, we introduce structured semigroups in Section 2.3, a generalisation of inverse semigroups that encompasses our primary motivating examples, namely the normaliser semigroups of Cartan subalgebras of C*-algebras.
In Section 3 we introduce groupoid bundles and examine their slice-sections. We give further motivational comments at the end to indicate how we construct groupoid bundles on which to represent structured semigroups.
Next in Section 4 we discuss appropriate morphisms between étale groupoids and groupoid bundles. Specifically, we consider relational Zakrzewski morphisms between étale groupoids, which are needed to include both continuous functions and group homomorphisms (but in opposite directions; see Remark 4.7), as well as the filter-coset Zakrzewski morphism
![]() $\vartriangleleft $
appearing later in Section 12.1. Building on these, we consider Zakrzewski–Pierce morphisms between groupoid bundles, which we show in Theorem 4.10 correspond to semigroup homomorphisms of their slice-sections.
$\vartriangleleft $
appearing later in Section 12.1. Building on these, we consider Zakrzewski–Pierce morphisms between groupoid bundles, which we show in Theorem 4.10 correspond to semigroup homomorphisms of their slice-sections.
From Section 5 we make the standing assumption that
![]() $(S,N,Z)$
is a structured semigroup. We then introduce the domination relation, a generalisation of the usual ordering on an inverse semigroup which also has analogous properties that we proceed to examine. Next, in Section 6, we introduce dual subsets as something of a substitute for inverses. Optimal results here require an additional diagonality assumption on N that we discuss in Section 6.1, which becomes more relevant again later in Section 12.
$(S,N,Z)$
is a structured semigroup. We then introduce the domination relation, a generalisation of the usual ordering on an inverse semigroup which also has analogous properties that we proceed to examine. Next, in Section 6, we introduce dual subsets as something of a substitute for inverses. Optimal results here require an additional diagonality assumption on N that we discuss in Section 6.1, which becomes more relevant again later in Section 12.
Continuing on the path of extending inverse semigroup theory, we introduce atlases and cosets in Section 7. In Section 8 we show that the cosets form an étale groupoid; see Theorem 8.4. Again optimal results require an additional assumption, namely that Z is ‘symmetric’, as discussed in Section 8.1. Under this assumption, we use cosets to construct a universal étale representation in Theorem 8.11.
In Sections 9 and 10 we show how to split up cosets into certain equivalence classes. The main result is Theorem 10.2, which says that these form an étale bundle. Next, we represent S on this coset bundle in Section 11. The main result here is Theorem 11.2, which says that this is a universal bundle representation, assuming symmetry.
Finally, in Section 12, we take a closer look at filters or, more accurately, directed cosets. These are shown to form an étale subgroupoid of the coset groupoid which instead yield Zakrzewski universal representations (again under symmetry), as shown in Theorems 12.15 and 12.18.
2 Motivation
2.1 Semilattices
To put our results in context, it is instructive to first consider semilattices, that is, commutative semigroups consisting entirely of idempotents. For example, the open subsets
![]() $\mathcal {O}(X)$
of any topological space X form a semilattice under the intersection operation
$\mathcal {O}(X)$
of any topological space X form a semilattice under the intersection operation
![]() $\cap $
. Of course the same applies to any subfamily of
$\cap $
. Of course the same applies to any subfamily of
![]() $\mathcal {O}(X)$
that is closed under pairwise intersections, like the family of open intervals
$\mathcal {O}(X)$
that is closed under pairwise intersections, like the family of open intervals
![]() $(a,b)$
on the real line
$(a,b)$
on the real line
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
A slightly less trivial observation is that, in fact, all semilattices are of this form, at least up to isomorphism. Put another way, every semilattice has a faithful spatial representation. Formally, a spatial representation of a semilattice S on a space X is a map
![]() $\theta :S\rightarrow \mathcal {O}(X)$
such that
$\theta :S\rightarrow \mathcal {O}(X)$
such that
![]() $\theta [S]$
covers X and, for all
$\theta [S]$
covers X and, for all
![]() $a,b\in S$
,
$a,b\in S$
,
A representation is faithful if it is injective, that is,
![]() $\theta (a)=\theta (b)$
if and only if
$\theta (a)=\theta (b)$
if and only if
![]() $a=b$
.
$a=b$
.
To construct a faithful representation of any given semilattice S, we can consider its filters, that is, those subsets
![]() $F\subseteq S$
such that, for all
$F\subseteq S$
such that, for all
![]() $a,b\in S$
,
$a,b\in S$
,
These are just the down-directed up-sets with respect to the order on S defined by
(as products in S are meets/infima with respect to this ordering). Let
![]() $\mathcal {F}(S)$
denote the filter spectrum, that is, the space of all nonempty filters with the basis
$\mathcal {F}(S)$
denote the filter spectrum, that is, the space of all nonempty filters with the basis
![]() $(\mathcal {F}_a)_{a\in S}$
, where
$(\mathcal {F}_a)_{a\in S}$
, where
Let
![]() $\mathcal {F}$
on its own denote the map
$\mathcal {F}$
on its own denote the map
![]() $a\mapsto \mathcal {F}_a$
.
$a\mapsto \mathcal {F}_a$
.
Proposition 2.1. The map
![]() $\mathcal {F}$
is a faithful spatial representation of S.
$\mathcal {F}$
is a faithful spatial representation of S.
Proof. We immediately note that
![]() $\mathcal {F}_{ab}=\mathcal {F}_a\cap \mathcal {F}_b$
, for all
$\mathcal {F}_{ab}=\mathcal {F}_a\cap \mathcal {F}_b$
, for all
![]() $a,b\in S$
, thanks to the defining property of filters, that is,
$a,b\in S$
, thanks to the defining property of filters, that is,
![]() $\mathcal {F}$
is a spatial representation. To see that
$\mathcal {F}$
is a spatial representation. To see that
![]() $\mathcal {F}$
is also faithful, first note that, for each
$\mathcal {F}$
is also faithful, first note that, for each
![]() $a\in S$
, there is a minimal filter containing a, namely
$a\in S$
, there is a minimal filter containing a, namely
Thus, for any
![]() $a,b\in S$
,
$a,b\in S$
,
![]() $\mathcal {F}_a=\mathcal {F}_b$
would imply
$\mathcal {F}_a=\mathcal {F}_b$
would imply
![]() $a^{\leq }\in \mathcal {F}_a=\mathcal {F}_b$
and
$a^{\leq }\in \mathcal {F}_a=\mathcal {F}_b$
and
![]() $b^{\leq }\in \mathcal {F}_b=\mathcal {F}_a$
, that is,
$b^{\leq }\in \mathcal {F}_b=\mathcal {F}_a$
, that is,
![]() $b\in a^{\leq }$
and
$b\in a^{\leq }$
and
![]() $a\in b^{\leq }$
and hence
$a\in b^{\leq }$
and hence
![]() $a=ab=b$
.
$a=ab=b$
.
We call
![]() $\mathcal {F}$
the filter representation of S. Note, however, that this is not the only faithful representation. Indeed, the proof above shows that the subrepresentation obtained by restricting to principal filters (of the form
$\mathcal {F}$
the filter representation of S. Note, however, that this is not the only faithful representation. Indeed, the proof above shows that the subrepresentation obtained by restricting to principal filters (of the form
![]() $a^{\leq }$
) is still faithful. What distinguishes the filter representation is its universality.
$a^{\leq }$
) is still faithful. What distinguishes the filter representation is its universality.
Roughly speaking, this means that the filter representation contains all possible spatial representations. To be more precise, first note that any continuous function
![]() $\phi :Y\rightarrow X$
between topological spaces X and Y defines a semilattice homomorphism
$\phi :Y\rightarrow X$
between topological spaces X and Y defines a semilattice homomorphism
![]() $\overline \phi :\mathcal {O}(X)\rightarrow \mathcal {O}(Y)$
(in the opposite direction) by taking preimages, that is,
$\overline \phi :\mathcal {O}(X)\rightarrow \mathcal {O}(Y)$
(in the opposite direction) by taking preimages, that is,
In particular, if
![]() $\theta :S\rightarrow \mathcal {O}(X)$
is a spatial representation and
$\theta :S\rightarrow \mathcal {O}(X)$
is a spatial representation and
![]() $\phi :Y\rightarrow X$
is a continuous map on another space Y, then we immediately obtain a spatial representation
$\phi :Y\rightarrow X$
is a continuous map on another space Y, then we immediately obtain a spatial representation
![]() $\overline \phi \circ \theta $
on Y by simply composing
$\overline \phi \circ \theta $
on Y by simply composing
![]() $\theta $
with
$\theta $
with
![]() $\overline \phi $
, that is, for all
$\overline \phi $
, that is, for all
![]() $a\in S$
,
$a\in S$
,
We call a spatial representation
![]() $\mu :S\rightarrow \mathcal {O}(X)$
universal if every spatial representation
$\mu :S\rightarrow \mathcal {O}(X)$
universal if every spatial representation
![]() $\theta :S\rightarrow \mathcal {O}(Y)$
can be written uniquely as such a composition, that is, if there exists a unique continuous map
$\theta :S\rightarrow \mathcal {O}(Y)$
can be written uniquely as such a composition, that is, if there exists a unique continuous map
![]() $\phi :Y\rightarrow X$
such that
$\phi :Y\rightarrow X$
such that
![]() $\theta =\overline \phi \circ \mu $
.
$\theta =\overline \phi \circ \mu $
.
Proposition 2.2. The filter representation
![]() $\mathcal {F}$
of any semilattice S is universal.
$\mathcal {F}$
of any semilattice S is universal.
Proof. Take a spatial representation
![]() $\theta :S\rightarrow \mathcal {O}(X)$
. For all
$\theta :S\rightarrow \mathcal {O}(X)$
. For all
![]() $x\in X$
, let
$x\in X$
, let
Note that
![]() $a,b\in \phi (x)$
if and only if
$a,b\in \phi (x)$
if and only if
![]() $x\in \theta (a)\cap \theta (b)=\theta (ab)$
if and only if
$x\in \theta (a)\cap \theta (b)=\theta (ab)$
if and only if
![]() $ab\in \phi (x)$
, showing that
$ab\in \phi (x)$
, showing that
![]() $\phi (x)$
is a filter. Moreover,
$\phi (x)$
is a filter. Moreover,
![]() $\phi (x)$
is also nonempty, as
$\phi (x)$
is also nonempty, as
![]() $\theta [S]$
covers X, so
$\theta [S]$
covers X, so
![]() $\phi (x)\in \mathcal {F}(S)$
. Further note that
$\phi (x)\in \mathcal {F}(S)$
. Further note that
![]() $\phi (x)\in \mathcal {F}_a$
if and only if
$\phi (x)\in \mathcal {F}_a$
if and only if
![]() $a\in \phi (x)$
if and only if
$a\in \phi (x)$
if and only if
![]() $x\in \theta (a)$
, and hence
$x\in \theta (a)$
, and hence
Thus,
![]() $\phi $
is a continuous map from X to
$\phi $
is a continuous map from X to
![]() $\mathcal {F}(S)$
with
$\mathcal {F}(S)$
with
![]() $\theta =\overline \phi \circ \mathcal {F}$
.
$\theta =\overline \phi \circ \mathcal {F}$
.
For uniqueness, suppose that we had another map
![]() $\phi ':X\rightarrow \mathcal {F}(S)$
such that
$\phi ':X\rightarrow \mathcal {F}(S)$
such that
![]() $\overline {\phi '}\circ \mathcal {F}=\theta $
, that is,
$\overline {\phi '}\circ \mathcal {F}=\theta $
, that is,
![]() $\phi ^{\prime -1}[\mathcal {F}_a]=\theta (a)$
, for all
$\phi ^{\prime -1}[\mathcal {F}_a]=\theta (a)$
, for all
![]() $a\in S$
. Then again we note that
$a\in S$
. Then again we note that
![]() $x\in \theta (a)$
if and only if
$x\in \theta (a)$
if and only if
![]() $\phi '(x)\in \mathcal {F}_a$
if and only if
$\phi '(x)\in \mathcal {F}_a$
if and only if
![]() $a\in \phi '(x)$
and hence
$a\in \phi '(x)$
and hence
![]() $\phi '(x)=\{a\in S:x\in \theta (a)\}=\phi (x)$
, for all
$\phi '(x)=\{a\in S:x\in \theta (a)\}=\phi (x)$
, for all
![]() $x\in X$
.
$x\in X$
.
Remark 2.3. The filter representation has various other subrepresentations that are of interest, particularly if one wants to represent semilattices on nicer topological spaces, for example with better separation properties.
For example, one could restrict to irreducible filters, which are always plentiful enough to retain faithfulness; see [Reference Celani8, Corollary 9]. The irreducible subrepresentation can even be extended to a categorical duality (see [Reference Celani and González9]) generalising the classic Stone duality between distributive lattices and spectral spaces (see [Reference Stone32]). The filter representation can also be extended to a different but analogous duality between semilattices and ‘HMS spaces’; see [Reference Jipsen and Andrew Moshier16].
One could also restrict to ultrafilters, that is, maximal proper filters, as in Wallman’s work; see [Reference Wallman34]. The space of ultrafilters is necessarily
![]() $T_1$
, although it is only faithful for special kinds of semilattices, for example, separative semilattices with
$T_1$
, although it is only faithful for special kinds of semilattices, for example, separative semilattices with
![]() $0$
. We also briefly examine ultrafilters in more general semigroups later in Theorem 12.8. Indeed, the present paper could be viewed as a prelude to our subsequent work in [Reference Bice2, Reference Bice3] where ultrafilters play a much greater role in noncommutative extensions of the classic Gelfand duality (see [Reference Gelfand13, Reference Gelfand and Naimark14]).
$0$
. We also briefly examine ultrafilters in more general semigroups later in Theorem 12.8. Indeed, the present paper could be viewed as a prelude to our subsequent work in [Reference Bice2, Reference Bice3] where ultrafilters play a much greater role in noncommutative extensions of the classic Gelfand duality (see [Reference Gelfand13, Reference Gelfand and Naimark14]).
2.2 Inverse semigroups
Our goal in the present paper is to extend Propositions 2.1 and 2.2 to noncommutative semigroups. As a first step in this direction, let us consider inverse semigroups S (see [Reference Lawson20]), that is, such that each
![]() $a\in S$
has a unique generalised inverse
$a\in S$
has a unique generalised inverse
![]() $a^{-1}$
, meaning that
$a^{-1}$
, meaning that
So semilattices are inverse semigroups where
![]() $a^{-1}=a$
. Also the idempotents
$a^{-1}=a$
. Also the idempotents
of any inverse semigroup S form a semilattice. Consequently, inverse semigroups constitute a natural noncommutative generalisation of semilattices.
Topological spaces also have a natural noncommutative generalisation, namely étale groupoids; see [Reference Renault26, Reference Sims29]. Let us digress for a moment to recall all the relevant definitions. First, a groupoid is a category where all the morphisms are isomorphisms. Following standard practice, we generally forget about the objects and just consider groupoids as collections of morphisms on which we have an inverse operation and a partially defined product. The units of a groupoid G are given by
We denote the source and range units of any
![]() $g\in G$
by
$g\in G$
by
Note that
![]() $gh$
is defined if and only if
$gh$
is defined if and only if
![]() $(g,h)\in G^2$
, where
$(g,h)\in G^2$
, where
As usual, we call
![]() $B\subseteq G$
a bisection or slice of a groupoid G if the source and range
$B\subseteq G$
a bisection or slice of a groupoid G if the source and range
![]() $\mathsf {s},\mathsf {r}:G\rightarrow G^0$
are injective on B or, equivalently, if
$\mathsf {s},\mathsf {r}:G\rightarrow G^0$
are injective on B or, equivalently, if
![]() $BB^{-1}\cup B^{-1}B\subseteq G^0$
, where
$BB^{-1}\cup B^{-1}B\subseteq G^0$
, where
![]() $B^{-1}=\{b^{-1}:b\in B\}$
and
$B^{-1}=\{b^{-1}:b\in B\}$
and
![]() $AB=\{ab:a\in A\text { and }b\in B\}$
.
$AB=\{ab:a\in A\text { and }b\in B\}$
.
A topological groupoid is a groupoid G with a topology which makes the inverse
![]() $g\mapsto g^{-1}$
and product
$g\mapsto g^{-1}$
and product
![]() $(g,h)\mapsto gh$
continuous (on
$(g,h)\mapsto gh$
continuous (on
![]() $G^2$
). A topological groupoid is étale if the source
$G^2$
). A topological groupoid is étale if the source
![]() $\mathsf {s}$
(and hence the range
$\mathsf {s}$
(and hence the range
![]() $\mathsf {r}$
and product too) is also an open map, that is,
$\mathsf {r}$
and product too) is also an open map, that is,
![]() $\mathsf {s}$
maps open subsets of G to open subsets of G (which, in particular, implies that the units
$\mathsf {s}$
maps open subsets of G to open subsets of G (which, in particular, implies that the units
![]() $G^0=\mathsf {s}[G]$
form an open subset). Equivalently, a topology makes a groupoid étale precisely when the open bisections
$G^0=\mathsf {s}[G]$
form an open subset). Equivalently, a topology makes a groupoid étale precisely when the open bisections
form both a basis for the topology of G and an inverse semigroup under pointwise products
![]() $(A,B)\mapsto AB$
and inverses
$(A,B)\mapsto AB$
and inverses
![]() $B\mapsto B^{-1}$
; see [Reference Resende28, Theorem 5.18] and [Reference Bice and Starling5, Proposition 6.6]. This characterisation suggests that étale groupoids are natural structures on which to represent inverse semigroups.
$B\mapsto B^{-1}$
; see [Reference Resende28, Theorem 5.18] and [Reference Bice and Starling5, Proposition 6.6]. This characterisation suggests that étale groupoids are natural structures on which to represent inverse semigroups.
Accordingly, we call a map
![]() $\theta :S\rightarrow \mathcal {B}(G)$
an étale representation of an inverse semigroup S if
$\theta :S\rightarrow \mathcal {B}(G)$
an étale representation of an inverse semigroup S if
![]() $\theta [S]$
covers the étale groupoid G and, for all
$\theta [S]$
covers the étale groupoid G and, for all
![]() $a,b\in S$
,
$a,b\in S$
,
(note that this is consistent with our previous notion of a spatial representation, as
![]() $AB=A\cap B$
for any
$AB=A\cap B$
for any
![]() $A,B\subseteq G^0$
, in particular for any
$A,B\subseteq G^0$
, in particular for any
![]() $A,B\in \mathcal {O}(X)$
when we consider a space X as an étale groupoid with the trivial product
$A,B\in \mathcal {O}(X)$
when we consider a space X as an étale groupoid with the trivial product
![]() $xx=x$
, for all
$xx=x$
, for all
![]() $x\in X$
). To obtain a faithful étale representation of an inverse semigroup S we can again consider filters with respect to the canonical ordering on S given by
$x\in X$
). To obtain a faithful étale representation of an inverse semigroup S we can again consider filters with respect to the canonical ordering on S given by
As before, we let
![]() $\mathcal {F}(S)$
denote the nonempty filters in S, that is, the down-directed up-sets. These form an étale groupoid with inverse
$\mathcal {F}(S)$
denote the nonempty filters in S, that is, the down-directed up-sets. These form an étale groupoid with inverse
![]() $F\mapsto F^{-1}$
and product
$F\mapsto F^{-1}$
and product
where
![]() $T^{\leq }=\{s\geq t:t\in T\}$
and the topology again has basis
$T^{\leq }=\{s\geq t:t\in T\}$
and the topology again has basis
![]() $(\mathcal {F}_a)_{a\in S}$
, where
$(\mathcal {F}_a)_{a\in S}$
, where
![]() $\mathcal {F}_a=\{F\in \mathcal {F}(S):a\in F\}$
; see [Reference Bice1, Propositions 2.7 and 2.38, Example 2.12 and Theorem 2.32], which extend results from [Reference Lawson and Lenz22, Reference Lawson, Margolis and Steinberg23]. We call
$\mathcal {F}_a=\{F\in \mathcal {F}(S):a\in F\}$
; see [Reference Bice1, Propositions 2.7 and 2.38, Example 2.12 and Theorem 2.32], which extend results from [Reference Lawson and Lenz22, Reference Lawson, Margolis and Steinberg23]. We call
![]() $\mathcal {F}(S)$
with this étale groupoid structure the filter groupoid of S. Again we let
$\mathcal {F}(S)$
with this étale groupoid structure the filter groupoid of S. Again we let
![]() $\mathcal {F}$
on its own denote the map
$\mathcal {F}$
on its own denote the map
![]() $a\mapsto \mathcal {F}_a$
.
$a\mapsto \mathcal {F}_a$
.
Proposition 2.4. The map
![]() $\mathcal {F}$
is a faithful étale representation of S.
$\mathcal {F}$
is a faithful étale representation of S.
Proof. For any
![]() $a,b\in S$
, we immediately see that
$a,b\in S$
, we immediately see that
![]() $\mathcal {F}_a\cdot \mathcal {F}_b\subseteq \mathcal {F}_{ab}$
. Conversely, for any
$\mathcal {F}_a\cdot \mathcal {F}_b\subseteq \mathcal {F}_{ab}$
. Conversely, for any
![]() $F\in \mathcal {F}_{ab}$
, set
$F\in \mathcal {F}_{ab}$
, set
![]() $E=(Fb^{-1})^{\leq }\in \mathcal {F}_a$
, as
$E=(Fb^{-1})^{\leq }\in \mathcal {F}_a$
, as
![]() $a\geq abb^{-1}\in Fb^{-1}$
. For any
$a\geq abb^{-1}\in Fb^{-1}$
. For any
![]() $s,t\in S$
and
$s,t\in S$
and
![]() $e\in \mathsf {E}(S)$
, we see that
$e\in \mathsf {E}(S)$
, we see that
![]() $set\leq st$
and hence
$set\leq st$
and hence
For the reverse inclusion, first note that
![]() $FF^{-1}F\subseteq F^{\leq }=F$
: for any
$FF^{-1}F\subseteq F^{\leq }=F$
: for any
![]() $f,g,h\in F$
, we have
$f,g,h\in F$
, we have
![]() $i\in F$
with
$i\in F$
with
![]() $i\leq f,g,h$
, as F is a filter, and hence
$i\leq f,g,h$
, as F is a filter, and hence
![]() $i=ii^{-1}i\leq fg^{-1}h$
. Thus,
$i=ii^{-1}i\leq fg^{-1}h$
. Thus,
As above, it then follows that
![]() $(EE^{-1})^{\leq }\subseteq (Ebb^{-1}E^{-1})^{\leq }\subseteq (FF^{-1})^{\leq }$
. Thus,
$(EE^{-1})^{\leq }\subseteq (Ebb^{-1}E^{-1})^{\leq }\subseteq (FF^{-1})^{\leq }$
. Thus,
![]() $E^{-1}\cdot F$
is defined and
$E^{-1}\cdot F$
is defined and
Thus,
![]() $\mathcal {F}_{ab}=\mathcal {F}_a\cdot \mathcal {F}_b$
, showing that
$\mathcal {F}_{ab}=\mathcal {F}_a\cdot \mathcal {F}_b$
, showing that
![]() $a\mapsto \mathcal {F}_a$
is indeed an étale representation. As before, we see that
$a\mapsto \mathcal {F}_a$
is indeed an étale representation. As before, we see that
![]() $\mathcal {F}$
is faithful by considering principal filters.
$\mathcal {F}$
is faithful by considering principal filters.
Of course, this is still not the only faithful étale representation and one would expect the filter representation again to be distinguished by its universality. However, universality fails, at least with respect to the obvious morphisms.
Specifically, we call a map
![]() $\phi :G\rightarrow H$
between étale groupoids an étale morphism if
$\phi :G\rightarrow H$
between étale groupoids an étale morphism if
![]() $\phi $
is a continuous star-bijective functor. Here star-bijectivity means that
$\phi $
is a continuous star-bijective functor. Here star-bijectivity means that
![]() $\phi $
maps each star
$\phi $
maps each star
![]() $Ge$
, for
$Ge$
, for
![]() $e\in G^0$
, bijectively on the corresponding star
$e\in G^0$
, bijectively on the corresponding star
![]() $H\phi (e)$
(see [Reference Brown7], [Reference Higgins15, Ch. 13]; star-bijective functors are also called covering functors in [Reference Lawson21]). As noted below in Section 4, star-bijectivity ensures that preimages of slices are slices and that preimages respect products, that is, for all
$H\phi (e)$
(see [Reference Brown7], [Reference Higgins15, Ch. 13]; star-bijective functors are also called covering functors in [Reference Lawson21]). As noted below in Section 4, star-bijectivity ensures that preimages of slices are slices and that preimages respect products, that is, for all
![]() $A,B\in \mathcal {B}(G)$
,
$A,B\in \mathcal {B}(G)$
,
Thus, any étale morphism
![]() $\phi :H\rightarrow G$
again defines a semigroup homomorphism
$\phi :H\rightarrow G$
again defines a semigroup homomorphism
![]() $\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
(in the opposite direction) between their open slice semigroups by just taking preimages. Composing
$\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
(in the opposite direction) between their open slice semigroups by just taking preimages. Composing
![]() $\overline \phi $
with any étale representation
$\overline \phi $
with any étale representation
![]() $\theta :S\rightarrow \mathcal {B}(G)$
on G then yields an étale representation
$\theta :S\rightarrow \mathcal {B}(G)$
on G then yields an étale representation
![]() $\overline \phi \circ \theta :S\rightarrow \mathcal {B}(H)$
on H.
$\overline \phi \circ \theta :S\rightarrow \mathcal {B}(H)$
on H.
Just like before, we call an étale representation
![]() $\mu :S\rightarrow \mathcal {B}(G)$
universal if every étale representation
$\mu :S\rightarrow \mathcal {B}(G)$
universal if every étale representation
![]() $\theta :S\rightarrow \mathcal {B}(H)$
can be written uniquely as such a composition, that is, there exists a unique étale morphism
$\theta :S\rightarrow \mathcal {B}(H)$
can be written uniquely as such a composition, that is, there exists a unique étale morphism
![]() $\phi :H\rightarrow G$
such that
$\phi :H\rightarrow G$
such that
![]() $\theta =\overline \phi \circ \mu $
. To see why the proof of Proposition 2.2 no longer works note that, while it is still possible to define
$\theta =\overline \phi \circ \mu $
. To see why the proof of Proposition 2.2 no longer works note that, while it is still possible to define
![]() ${\phi (g)=\{a\in S:g\in \theta (a)\}}$
, this may not be a filter anymore. To construct universal representations here we must consider a slightly broader inverse semigroup generalisation of filters in semilattices.
${\phi (g)=\{a\in S:g\in \theta (a)\}}$
, this may not be a filter anymore. To construct universal representations here we must consider a slightly broader inverse semigroup generalisation of filters in semilattices.
Specifically, we call
![]() $C\subseteq S$
a coset if, for all
$C\subseteq S$
a coset if, for all
![]() $a,b\in C$
and
$a,b\in C$
and
![]() $c\in S$
,
$c\in S$
,
Equivalently,
![]() $C\subseteq S$
is a coset when
$C\subseteq S$
is a coset when
![]() $C=C^{\leq }=CC^{-1}C$
; see [Reference Lawson20, §1.4, Proposition 26]. The nonempty cosets
$C=C^{\leq }=CC^{-1}C$
; see [Reference Lawson20, §1.4, Proposition 26]. The nonempty cosets
![]() $\mathcal {C}(S)$
again form an étale groupoid with inverse
$\mathcal {C}(S)$
again form an étale groupoid with inverse
![]() $C\mapsto C^{-1}$
, product
$C\mapsto C^{-1}$
, product
![]() $B\cdot C=(BC)^{\leq }$
and subbasis
$B\cdot C=(BC)^{\leq }$
and subbasis
![]() $(\mathcal {C}_a)_{a\in S}$
, where
$(\mathcal {C}_a)_{a\in S}$
, where
again see [Reference Bice1, Example 2.12 and Theorem 2.32]. We call
![]() $\mathcal {C}(S)$
with this étale groupoid structure the coset groupoid of S and again let
$\mathcal {C}(S)$
with this étale groupoid structure the coset groupoid of S and again let
![]() $\mathcal {C}$
denote the map
$\mathcal {C}$
denote the map
![]() $a\mapsto \mathcal {C}_a$
. As in the proof of Proposition 2.4, we see that
$a\mapsto \mathcal {C}_a$
. As in the proof of Proposition 2.4, we see that
![]() $\mathcal {C}$
is a faithful étale representation of S which we call the coset representation.
$\mathcal {C}$
is a faithful étale representation of S which we call the coset representation.
Proposition 2.5. The coset representation of any inverse semigroup S is universal.
Proof. Take any étale representation
![]() $\theta :S\rightarrow \mathcal {B}(G)$
. For
$\theta :S\rightarrow \mathcal {B}(G)$
. For
![]() $g\in G$
, define
$g\in G$
, define
If
![]() $a,b,c\in \phi (g)$
then
$a,b,c\in \phi (g)$
then
![]() $g=gg^{-1}g\in \theta (a)\theta (b)^{-1}\theta (c)=\theta (ab^{-1}c)$
, which means that
$g=gg^{-1}g\in \theta (a)\theta (b)^{-1}\theta (c)=\theta (ab^{-1}c)$
, which means that
![]() $ab^{-1}c\in \phi (g)$
. On the other hand, if
$ab^{-1}c\in \phi (g)$
. On the other hand, if
![]() $a,b,ab^{-1}c\in \phi (g)$
then
$a,b,ab^{-1}c\in \phi (g)$
then
So
![]() $\phi (g)$
is a coset, which is also nonempty, as
$\phi (g)$
is a coset, which is also nonempty, as
![]() $(\theta (a))_{a\in S}$
covers G, that is,
$(\theta (a))_{a\in S}$
covers G, that is,
![]() $\phi (g)\in \mathcal {C}(S)$
.
$\phi (g)\in \mathcal {C}(S)$
.
Next, note that
![]() $\phi (\mathsf {s}(g))=\mathsf {s}(\phi (g))$
. Indeed, we immediately see that
$\phi (\mathsf {s}(g))=\mathsf {s}(\phi (g))$
. Indeed, we immediately see that
Conversely, for any
![]() $a\in \phi (\mathsf {s}(g))$
, taking
$a\in \phi (\mathsf {s}(g))$
, taking
![]() $b\in \phi (g)$
, we see that
$b\in \phi (g)$
, we see that
![]() $a\geq ab^{-1}b\in \phi (g^{-1})\phi (g)$
and hence
$a\geq ab^{-1}b\in \phi (g^{-1})\phi (g)$
and hence
![]() $a\in (\phi (g^{-1})\phi (g))^{\leq }=\phi (g^{-1})\cdot \phi (g)=\phi (\mathsf {s}(g))$
, that is,
$a\in (\phi (g^{-1})\phi (g))^{\leq }=\phi (g^{-1})\cdot \phi (g)=\phi (\mathsf {s}(g))$
, that is,
![]() $\phi (\mathsf {s}(g))\subseteq \mathsf {s}(\phi (g))$
. Likewise,
$\phi (\mathsf {s}(g))\subseteq \mathsf {s}(\phi (g))$
. Likewise,
![]() $\phi (\mathsf {r}(g))=\mathsf {r}(\phi (g))$
so
$\phi (\mathsf {r}(g))=\mathsf {r}(\phi (g))$
so
![]() $\mathsf {s}(g)=\mathsf {r}(h)$
implies that
$\mathsf {s}(g)=\mathsf {r}(h)$
implies that
![]() $\mathsf {s}(\phi (g))=\mathsf {r}(\phi (h))$
, so
$\mathsf {s}(\phi (g))=\mathsf {r}(\phi (h))$
, so
![]() $\phi (g)\cdot \phi (h)$
is a valid product. Again
$\phi (g)\cdot \phi (h)$
is a valid product. Again
![]() $\phi (g)\cdot \phi (h)\subseteq \phi (gh)$
is immediate, while the reverse inclusion follows as above. Thus,
$\phi (g)\cdot \phi (h)\subseteq \phi (gh)$
is immediate, while the reverse inclusion follows as above. Thus,
![]() $\phi $
is a functor.
$\phi $
is a functor.
To show that
![]() $\phi $
is star-bijective, take any
$\phi $
is star-bijective, take any
![]() $i\in G^0$
. If
$i\in G^0$
. If
![]() $\mathsf {s}(g)=\mathsf {s}(h)=i$
and
$\mathsf {s}(g)=\mathsf {s}(h)=i$
and
![]() $\phi (g)=\phi (h)$
then, for any
$\phi (g)=\phi (h)$
then, for any
![]() $a\in \phi (g)=\phi (h)$
, we see that
$a\in \phi (g)=\phi (h)$
, we see that
![]() $g,h\in \theta (a)$
and hence
$g,h\in \theta (a)$
and hence
![]() $g=h$
, as
$g=h$
, as
![]() $\theta (a)$
is a slice, showing that
$\theta (a)$
is a slice, showing that
![]() $\phi $
is star-injective. On the other hand, for any
$\phi $
is star-injective. On the other hand, for any
![]() $C\in \mathcal {C}(S)$
with
$C\in \mathcal {C}(S)$
with
![]() $\mathsf {s}(C)=\phi (i)$
, taking
$\mathsf {s}(C)=\phi (i)$
, taking
![]() $c\in C$
, we see that
$c\in C$
, we see that
![]() $c^{-1}c\in C^{-1}C\subseteq \mathsf {s}(C)=\phi (i)$
and hence
$c^{-1}c\in C^{-1}C\subseteq \mathsf {s}(C)=\phi (i)$
and hence
![]() $i\in \theta (c^{-1}c)=\theta (c)^{-1}\theta (c)=\mathsf {s}[\theta (c)]$
, as
$i\in \theta (c^{-1}c)=\theta (c)^{-1}\theta (c)=\mathsf {s}[\theta (c)]$
, as
![]() $\theta (c)$
is a slice. Thus, we have
$\theta (c)$
is a slice. Thus, we have
![]() $g\in \theta (c)$
with
$g\in \theta (c)$
with
![]() $\mathsf {s}(g)=i$
and hence
$\mathsf {s}(g)=i$
and hence
by [Reference Bice1, Theorem 2.32], proving that
![]() $\phi $
is also star-surjective.
$\phi $
is also star-surjective.
For continuity note that, as before,
![]() $\phi (g)\in \mathcal {C}_a$
if and only if
$\phi (g)\in \mathcal {C}_a$
if and only if
![]() $a\in \phi (g)$
if and only if
$a\in \phi (g)$
if and only if
![]() $g\in \theta (a)$
, so
$g\in \theta (a)$
, so
Thus,
![]() $\phi $
is an étale morphism from G to
$\phi $
is an étale morphism from G to
![]() $\mathcal {C}(S)$
with
$\mathcal {C}(S)$
with
![]() $\theta =\overline \phi \circ \mathcal {C}$
. Uniqueness follows by the same argument as before.
$\theta =\overline \phi \circ \mathcal {C}$
. Uniqueness follows by the same argument as before.
As hinted at above, there is actually an alternative approach here: instead of broadening the class of filters, we can broaden the class of étale morphisms. Specifically, we can consider more general relational Zakrzewski morphisms between étale groupoids; see Section 4 below. Indeed, there is a Zakrzewski morphism between filters and cosets of any inverse semigroup, which can be used to show that the filter representation is universal with respect to Zakrzewski morphisms (see Theorems 12.14 and 12.15 below for more general structured semigroup results).
2.3 Structured semigroups
The only problem with inverse semigroups is that they are not general enough, not if we want to apply the theory to semigroups commonly arising in other fields. Our primary motivating examples here come from operator algebras, where Cartan subalgebras of C*-algebras have received increasing attention in recent years; see [Reference Renault27]. A key role in their theory is played by the normaliser semigroup S of a Cartan subalgebra
![]() $C\subseteq A$
given by
$C\subseteq A$
given by
Note that if A is a projectionless C*-algebra, like the well-known Jiang–Su algebra (which does indeed have Cartan subalgebras; see [Reference Deeley, Putnam and Strung11]), then S cannot contain any nontrivial idempotents and thus certainly cannot be an inverse semigroup. Even when A does have a large supply of projections, for example, when A has real rank zero, there is still no guarantee that they will lie in S.
However, the Cartan subalgebra C here is a subsemigroup of S which still behaves much like the idempotents in an inverse semigroup. For one thing, C is commutative, and its self-adjoint part
![]() $C_{\mathrm {sa}}=\{a\in C:a=a^*\}$
also has a natural lattice structure. This exposes the possibility that inverse semigroup techniques could still be applied to Cartan pairs if we could somehow extend the relevant theory to *-semigroups S with a sufficiently well-behaved *-subsemigroup C. This is precisely what we did in our previous paper [Reference Bice1], where we examined ‘Weyl *-semigroups’ and their coset and filter groupoids.
$C_{\mathrm {sa}}=\{a\in C:a=a^*\}$
also has a natural lattice structure. This exposes the possibility that inverse semigroup techniques could still be applied to Cartan pairs if we could somehow extend the relevant theory to *-semigroups S with a sufficiently well-behaved *-subsemigroup C. This is precisely what we did in our previous paper [Reference Bice1], where we examined ‘Weyl *-semigroups’ and their coset and filter groupoids.
In the present paper we have our eye on applications even further afield (see [Reference Bice2, Reference Bice3]), namely to algebraic analogues of C*-algebras known as Steinberg algebras (see [Reference Clark, Farthing, Sims and Tomforde10, Reference Steinberg31]) as well as to noncommutative Cartan subalgebras of C*-algebras (see [Reference Exel12, Reference Kwaśniewski and Meyer19]). This forces us to consider more general semigroups S without an involution
![]() $^*$
, with more general noncommutative subsemigroups C. But we can always replace C with its centre
$^*$
, with more general noncommutative subsemigroups C. But we can always replace C with its centre
or some fixed subsemigroup Z, whenever commutativity is vital.
This naturally leads us to the concept of a ‘structured semigroup’. Formally this a triple
![]() $(S,N,Z)$
where S is a semigroup with distinguished subsemigroups N and
$(S,N,Z)$
where S is a semigroup with distinguished subsemigroups N and
![]() $Z\subseteq \mathsf {Z}(N)$
satisfying certain weak normality conditions. To describe these conditions, first recall that
$Z\subseteq \mathsf {Z}(N)$
satisfying certain weak normality conditions. To describe these conditions, first recall that
![]() $N\subseteq S$
is said to be normal if, for all
$N\subseteq S$
is said to be normal if, for all
![]() $s\in S$
,
$s\in S$
,
Let us call
![]() $Z\subseteq S$
binormal if, for all
$Z\subseteq S$
binormal if, for all
![]() $a,b\in S$
,
$a,b\in S$
,
If N is another subset, we call it Z-trinormal if, for all
![]() $a,b\in S$
and
$a,b\in S$
and
![]() $n\in N$
,
$n\in N$
,
Note that if
![]() $Z\subseteq \mathsf {Z}(N)$
, as in the structured semigroups considered below, then we always have
$Z\subseteq \mathsf {Z}(N)$
, as in the structured semigroups considered below, then we always have
![]() $abn=nab$
whenever
$abn=nab$
whenever
![]() $ab\in Z$
and
$ab\in Z$
and
![]() $n\in N$
. So, in this case, the left side of (
Z-Trinormal) could be replaced with just
$n\in N$
. So, in this case, the left side of (
Z-Trinormal) could be replaced with just
![]() $abn=n$
.
$abn=n$
.
Definition 2.6. We call
![]() $(S,N,Z)$
a structured semigroup if:
$(S,N,Z)$
a structured semigroup if:
(1) S is a semigroup;
(2) N is a Z-trinormal subsemigroup of S;
(3)
 $Z\subseteq \mathsf {Z}(N)$
is a binormal subsemigroup of S.
$Z\subseteq \mathsf {Z}(N)$
is a binormal subsemigroup of S.
Note that every normal subsemigroup Z is binormal, as
![]() $ab\in Z$
then implies
$ab\in Z$
then implies
![]() $aZb=abZ\subseteq ZZ\subseteq Z$
. However, the converse can fail; for example, Cartan subalgebras are always binormal in their normaliser semigroups, even though they are not necessarily normal (see [Reference Bice and Clark4, Example 7.3]). Similarly, we also immediately see that any binormal N is N-trinormal and hence Z-trinormal, for any
$aZb=abZ\subseteq ZZ\subseteq Z$
. However, the converse can fail; for example, Cartan subalgebras are always binormal in their normaliser semigroups, even though they are not necessarily normal (see [Reference Bice and Clark4, Example 7.3]). Similarly, we also immediately see that any binormal N is N-trinormal and hence Z-trinormal, for any
![]() $Z\subseteq N$
. In particular, for any commutative binormal subsemigroup C of a semigroup S, we get a structured semigroup by simply taking
$Z\subseteq N$
. In particular, for any commutative binormal subsemigroup C of a semigroup S, we get a structured semigroup by simply taking
![]() $N=Z=C$
. This applies to any Cartan subalgebra C in its normaliser semigroup S, as well as to the idempotents in any inverse semigroup, thanks to the following observation.
$N=Z=C$
. This applies to any Cartan subalgebra C in its normaliser semigroup S, as well as to the idempotents in any inverse semigroup, thanks to the following observation.
Proposition 2.7. The idempotents
![]() $\mathsf {E}(S)$
of any inverse semigroup S are normal.
$\mathsf {E}(S)$
of any inverse semigroup S are normal.
Proof. For any
![]() $s\in S$
and
$s\in S$
and
![]() $e\in \mathsf {E}(S)$
, note that
$e\in \mathsf {E}(S)$
, note that
![]() $ses^{-1}ses^{-1}=ss^{-1}sees^{-1}=ses^{-1}$
, that is,
$ses^{-1}ses^{-1}=ss^{-1}sees^{-1}=ses^{-1}$
, that is,
![]() $ses^{-1}\in \mathsf {E}(S)$
. Moreover,
$ses^{-1}\in \mathsf {E}(S)$
. Moreover,
![]() $se=ss^{-1}se=ses^{-1}s$
, showing that
$se=ss^{-1}se=ses^{-1}s$
, showing that
![]() $s\mathsf {E}(S)\subseteq \mathsf {E}(S)s$
, while the reverse inclusion follows by a dual argument.
$s\mathsf {E}(S)\subseteq \mathsf {E}(S)s$
, while the reverse inclusion follows by a dual argument.
However, inverse semigroups can also form structured semigroups in other ways, that is, there may be other natural choices for N and Z; see, for example, Proposition 3.6 below.
The next question is how structured semigroups should be represented. As before, we could consider étale representations, that is, semigroup homomorphisms
![]() $\theta :S\rightarrow \mathcal {B}(G)$
, for some étale groupoid G. As N is meant to be a kind of diagonal of S, it would be natural to further require that
$\theta :S\rightarrow \mathcal {B}(G)$
, for some étale groupoid G. As N is meant to be a kind of diagonal of S, it would be natural to further require that
![]() $\theta $
maps N onto open subsets of the diagonal of G, that is, its unit space
$\theta $
maps N onto open subsets of the diagonal of G, that is, its unit space
![]() $G^0$
, as we do in Definition 8.9 below. However, these are the idempotents of
$G^0$
, as we do in Definition 8.9 below. However, these are the idempotents of
![]() $\mathcal {B}(G)$
, so if
$\mathcal {B}(G)$
, so if
![]() $\theta $
were also faithful then this would imply that N also consists entirely of idempotents. So again we see that these kinds of étale representations are not general enough, not if we want structured semigroups with few idempotents to potentially have faithful representations.
$\theta $
were also faithful then this would imply that N also consists entirely of idempotents. So again we see that these kinds of étale representations are not general enough, not if we want structured semigroups with few idempotents to potentially have faithful representations.
To fix this, we again take inspiration from operator algebra theory, specifically Kumjian and Renault’s Weyl groupoid construction from a Cartan pair
![]() $(A,C)$
; see [Reference Kumjian17, Reference Renault27]. This results in the C*-algebra A being represented as continuous sections of a saturated Fell line bundle
$(A,C)$
; see [Reference Kumjian17, Reference Renault27]. This results in the C*-algebra A being represented as continuous sections of a saturated Fell line bundle
![]() $\pi :F\rightarrow G$
over a locally compact étale groupoid G. Furthermore, the sections coming from the normaliser semigroup S are supported on open slices of G. Restricting to these supports yields a representation of S as partial sections defined on slices taking values in the groupoid
$\pi :F\rightarrow G$
over a locally compact étale groupoid G. Furthermore, the sections coming from the normaliser semigroup S are supported on open slices of G. Restricting to these supports yields a representation of S as partial sections defined on slices taking values in the groupoid
![]() $F^{\times }$
of invertible elements. This suggests that we should likewise represent more general structured semigroups as partial sections of groupoid bundles. Accordingly, we start the paper proper with a discussion of these bundles and their slice-sections.
$F^{\times }$
of invertible elements. This suggests that we should likewise represent more general structured semigroups as partial sections of groupoid bundles. Accordingly, we start the paper proper with a discussion of these bundles and their slice-sections.
3 Slice-sections
We assume that the reader is familiar with the basics of étale groupoids, as briefly outlined in the previous section. We refer the reader to [Reference Renault26, Reference Sims29] for further background, the key difference in our work being that our étale groupoids (and even their unit spaces) can be highly non-Hausdorff.
Recall that an isocofibration
![]() $\pi :C\rightarrow D$
between categories C and D is a functor that is injective on objects/units or, equivalently, such that
$\pi :C\rightarrow D$
between categories C and D is a functor that is injective on objects/units or, equivalently, such that
![]() $cd$
is defined in C whenever
$cd$
is defined in C whenever
![]() $\pi (c)\pi (d)$
is defined in D. Also a map
$\pi (c)\pi (d)$
is defined in D. Also a map
![]() $\pi :X\rightarrow Y$
on a topological space X is locally injective if every point in X has a neighbourhood on which
$\pi :X\rightarrow Y$
on a topological space X is locally injective if every point in X has a neighbourhood on which
![]() $\pi $
is injective or, equivalently, such that the open subsets of X on which
$\pi $
is injective or, equivalently, such that the open subsets of X on which
![]() $\pi $
is injective cover X.
$\pi $
is injective cover X.
Definition 3.1. We call
![]() $\pi :F\rightarrow G$
a groupoid bundle if:
$\pi :F\rightarrow G$
a groupoid bundle if:
(1) F is a topological groupoid;
(2) G is an étale groupoid; and
(3)
 $\pi $
is an open continuous isocofibration.
$\pi $
is an open continuous isocofibration.
An étale bundle is a groupoid bundle
![]() $\pi :F\rightarrow G$
that is also locally injective.
$\pi :F\rightarrow G$
that is also locally injective.
If
![]() $\pi :F\rightarrow G$
is an étale bundle then, in particular,
$\pi :F\rightarrow G$
is an étale bundle then, in particular,
![]() $\pi $
is an open continuous and locally injective map, that is, a local homeomorphism. In this case, the source map
$\pi $
is an open continuous and locally injective map, that is, a local homeomorphism. In this case, the source map
![]() $\mathsf {s}$
on F is also a local homeomorphism, which means that F is also an étale groupoid.
$\mathsf {s}$
on F is also a local homeomorphism, which means that F is also an étale groupoid.
Proposition 3.2. If
![]() $\pi :F\rightarrow G$
is an étale bundle then F is an étale groupoid.
$\pi :F\rightarrow G$
is an étale bundle then F is an étale groupoid.
Proof. Assume that
![]() $\pi :F\rightarrow G$
is an étale bundle. First we show that
$\pi :F\rightarrow G$
is an étale bundle. First we show that
![]() $F^0$
is open in F. To see this, take any
$F^0$
is open in F. To see this, take any
![]() $f\in F^0$
. As
$f\in F^0$
. As
![]() $\pi $
is locally injective, f has an open neighbourhood O on which
$\pi $
is locally injective, f has an open neighbourhood O on which
![]() $\pi $
is injective. We claim that
$\pi $
is injective. We claim that
To start with,
![]() $f\in F^0$
implies
$f\in F^0$
implies
![]() $\mathsf {s}(f)=f\in O$
and
$\mathsf {s}(f)=f\in O$
and
![]() $\pi (f)\in G^0$
, as
$\pi (f)\in G^0$
, as
![]() $\pi $
is a functor, showing that
$\pi $
is a functor, showing that
![]() $f\in O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
. On the other hand, for any
$f\in O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
. On the other hand, for any
![]() $e\in O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
, we see that
$e\in O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
, we see that
![]() $e,\mathsf {s}(e)\in O$
and
$e,\mathsf {s}(e)\in O$
and
![]() $\pi (e)=\mathsf {s}(\pi (e))=\pi (\mathsf {s}(e))$
and hence
$\pi (e)=\mathsf {s}(\pi (e))=\pi (\mathsf {s}(e))$
and hence
![]() $e=\mathsf {s}(e)\in F^0$
, as
$e=\mathsf {s}(e)\in F^0$
, as
![]() $\pi $
is injective on O, proving the claim. As
$\pi $
is injective on O, proving the claim. As
![]() $\mathsf {s}$
and
$\mathsf {s}$
and
![]() $\pi $
are continuous, and O and
$\pi $
are continuous, and O and
![]() $G^0$
are open, it follows that
$G^0$
are open, it follows that
![]() $O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
is also open. As f was arbitrary, this shows that
$O\cap \mathsf {s}^{-1}[O]\cap \pi ^{-1}[G^0]$
is also open. As f was arbitrary, this shows that
![]() $F^0$
is open.
$F^0$
is open.
As
![]() $\pi $
is injective on units, for any
$\pi $
is injective on units, for any
![]() $O\subseteq F$
,
$O\subseteq F$
,
If O is open then this shows that
![]() $\mathsf {s}[O]$
is also open, that is,
$\mathsf {s}[O]$
is also open, that is,
![]() $\mathsf {s}$
is an open map on F and hence F is an étale groupoid.
$\mathsf {s}$
is an open map on F and hence F is an étale groupoid.
The simplest examples of groupoid bundles come from the obvious structure on the Cartesian product of an étale groupoid and a topological group.
Example 3.3 (trivial bundles)
If G is an étale groupoid and T is a topological group then
![]() $G\times T$
is a topological groupoid in the product topology where
$G\times T$
is a topological groupoid in the product topology where
when
![]() $gh$
is defined. The projection
$gh$
is defined. The projection
![]() $\pi :G\times T\rightarrow G$
is then a groupoid bundle. If T is discrete then
$\pi :G\times T\rightarrow G$
is then a groupoid bundle. If T is discrete then
![]() $\pi $
is also locally injective and hence a local homeomorphism.
$\pi $
is also locally injective and hence a local homeomorphism.
More interesting ‘twisted’ bundles can be obtained by modifying the structure above via a given
![]() $2$
-cocycle, just like in [Reference Renault26] and [Reference Sims29, Section 5.1].
$2$
-cocycle, just like in [Reference Renault26] and [Reference Sims29, Section 5.1].
Example 3.4 (twisted bundles)
Again suppose that G is an étale groupoid and T is a topological group. Furthermore, suppose that
![]() $\sigma :G^2\mapsto T$
is a continuous
$\sigma :G^2\mapsto T$
is a continuous
![]() $2$
-cocycle, that is,
$2$
-cocycle, that is,
for all
![]() $g\in G$
, and, for all
$g\in G$
, and, for all
![]() $t\in T$
and
$t\in T$
and
![]() $g,h,i\in G$
such that
$g,h,i\in G$
such that
![]() $ghi$
is defined,
$ghi$
is defined,
We claim that
![]() $G\times T$
is a topological groupoid in the product topology, where this time
$G\times T$
is a topological groupoid in the product topology, where this time
when
![]() $gh$
is defined. Indeed, we verify associativity by noting that
$gh$
is defined. Indeed, we verify associativity by noting that
 $$ \begin{align*} [(g,t)(h,u)](i,v)&=(gh,t\sigma(g,h)u)(i,v)=(ghi,t\sigma(g,h)u\sigma(gh,i)v),\\ (g,t)[(h,u)(i,v)]&=(g,t)(hi,u\sigma(h,i)v)=(ghi,t\sigma(g,hi)u\sigma(h,i)v), \end{align*} $$
$$ \begin{align*} [(g,t)(h,u)](i,v)&=(gh,t\sigma(g,h)u)(i,v)=(ghi,t\sigma(g,h)u\sigma(gh,i)v),\\ (g,t)[(h,u)(i,v)]&=(g,t)(hi,u\sigma(h,i)v)=(ghi,t\sigma(g,hi)u\sigma(h,i)v), \end{align*} $$
where the last two expressions are equal by (3-1). Likewise, for all
![]() $g\in G$
,
$g\in G$
,
It follows that
 $$ \begin{align*} (g^{-1},\sigma(g,g^{-1})^{-1}t^{-1})(g,t)&=(\mathsf{s}(g),\sigma(g,g^{-1})^{-1}t^{-1}\sigma(g^{-1},g)t)\\ &=(\mathsf{s}(g),\sigma(g,g^{-1})^{-1}t^{-1}t\sigma(g,g^{-1}))\\ &=(\mathsf{s}(g),1) \end{align*} $$
$$ \begin{align*} (g^{-1},\sigma(g,g^{-1})^{-1}t^{-1})(g,t)&=(\mathsf{s}(g),\sigma(g,g^{-1})^{-1}t^{-1}\sigma(g^{-1},g)t)\\ &=(\mathsf{s}(g),\sigma(g,g^{-1})^{-1}t^{-1}t\sigma(g,g^{-1}))\\ &=(\mathsf{s}(g),1) \end{align*} $$
and, similarly,
![]() $(g,t)(g^{-1},\sigma (g,g^{-1})^{-1}t^{-1})=(\mathsf {r}(g),1)$
, that is,
$(g,t)(g^{-1},\sigma (g,g^{-1})^{-1}t^{-1})=(\mathsf {r}(g),1)$
, that is,
As the cocycle is continuous, so is the product and inverse on
![]() $G\times T$
. So again
$G\times T$
. So again
![]() $G\times T$
is a topological groupoid and
$G\times T$
is a topological groupoid and
![]() $\pi :G\times T\rightarrow G$
is a groupoid bundle.
$\pi :G\times T\rightarrow G$
is a groupoid bundle.
Our primary interest in groupoid bundles is that they form natural structures on which to represent semigroups as ‘slice-sections’.
Definition 3.5. A slice-section of a groupoid bundle
![]() $\pi :F\rightarrow G$
is a continuous map a where
$\pi :F\rightarrow G$
is a continuous map a where
![]() $\mathrm {dom}(a)$
is an open slice of G on which
$\mathrm {dom}(a)$
is an open slice of G on which
![]() $\pi \circ a$
is the identity.
$\pi \circ a$
is the identity.
So if a is a slice-section then
![]() $\mathrm {ran}(a)\subseteq F$
and
$\mathrm {ran}(a)\subseteq F$
and
![]() $\pi (a(g))=g$
, for
$\pi (a(g))=g$
, for
![]() $g\in \mathrm {dom}(a)$
.
$g\in \mathrm {dom}(a)$
.
Proposition 3.6. The slice-sections
![]() $\mathcal {S}(\pi )$
of a groupoid bundle
$\mathcal {S}(\pi )$
of a groupoid bundle
![]() $\pi :F\rightarrow G$
form an inverse semigroup where, for all
$\pi :F\rightarrow G$
form an inverse semigroup where, for all
![]() $a,b\in S$
, the product is given by
$a,b\in S$
, the product is given by
![]() $($
so
$($
so
![]() $\mathrm {dom}(ab)=\mathrm {dom}(a)\mathrm {dom}(b))$
. Moreover,
$\mathrm {dom}(ab)=\mathrm {dom}(a)\mathrm {dom}(b))$
. Moreover,
![]() $\mathcal {S}(\pi )$
has normal subsemigroups
$\mathcal {S}(\pi )$
has normal subsemigroups
 $$ \begin{align*} \mathcal{N}(\pi)&=\{n\in\mathcal{S}(\pi):\mathrm{dom}(n)\subseteq G^0\}, \\ \mathsf{E}(\mathcal{S}(\pi))&=\{z\in\mathcal{S}(\pi):\mathrm{ran}(z)\subseteq F^0\}\subseteq\mathsf{Z}(\mathcal{N}(\pi)). \end{align*} $$
$$ \begin{align*} \mathcal{N}(\pi)&=\{n\in\mathcal{S}(\pi):\mathrm{dom}(n)\subseteq G^0\}, \\ \mathsf{E}(\mathcal{S}(\pi))&=\{z\in\mathcal{S}(\pi):\mathrm{ran}(z)\subseteq F^0\}\subseteq\mathsf{Z}(\mathcal{N}(\pi)). \end{align*} $$
In particular,
![]() $(S,N,Z)=(\mathcal {S}(\pi ),\mathcal {N}(\pi ),\mathsf {E}(\mathcal {S}(\pi )))$
is a structured semigroup.
$(S,N,Z)=(\mathcal {S}(\pi ),\mathcal {N}(\pi ),\mathsf {E}(\mathcal {S}(\pi )))$
is a structured semigroup.
Proof. If
![]() $gh$
is defined in G, for some
$gh$
is defined in G, for some
![]() $g,h\in G$
, then
$g,h\in G$
, then
![]() $a(g)b(h)$
is also defined in G, as
$a(g)b(h)$
is also defined in G, as
![]() $\pi (a(g))=g$
,
$\pi (a(g))=g$
,
![]() $\pi (b(h))=h$
and
$\pi (b(h))=h$
and
![]() $\pi $
is an isocofibration. Also, for any
$\pi $
is an isocofibration. Also, for any
![]() $i\in G$
, we have at most one pair
$i\in G$
, we have at most one pair
![]() $g\in \mathrm {dom}(a)$
and
$g\in \mathrm {dom}(a)$
and
![]() $h\in \mathrm {dom}(b)$
with
$h\in \mathrm {dom}(b)$
with
![]() $gh=i$
, as these domains are slices. Thus, the above product yields a well-defined function
$gh=i$
, as these domains are slices. Thus, the above product yields a well-defined function
![]() $ab$
on the slice
$ab$
on the slice
![]() $\mathrm {dom}(ab)=\mathrm {dom}(a)\mathrm {dom}(b)$
. Furthermore, for any
$\mathrm {dom}(ab)=\mathrm {dom}(a)\mathrm {dom}(b)$
. Furthermore, for any
![]() $g,h\in H$
such that
$g,h\in H$
such that
![]() $gh$
is defined,
$gh$
is defined,
as
![]() $\pi $
is a functor, so again
$\pi $
is a functor, so again
![]() $\pi \circ ab$
is the identity on
$\pi \circ ab$
is the identity on
![]() $\mathrm {dom}(ab)$
. As the product in F is continuous, the function
$\mathrm {dom}(ab)$
. As the product in F is continuous, the function
![]() $ab$
is also continuous and hence a slice-section. As the inverse map in F is continuous, every slice-section a has a unique inverse slice-section
$ab$
is also continuous and hence a slice-section. As the inverse map in F is continuous, every slice-section a has a unique inverse slice-section
![]() $a^{-1}(g)=a(g^{-1})^{-1}$
, for all
$a^{-1}(g)=a(g^{-1})^{-1}$
, for all
![]() $g\in \mathrm {dom}(a)^{-1}$
. Thus, the slice-sections do indeed form an inverse semigroup
$g\in \mathrm {dom}(a)^{-1}$
. Thus, the slice-sections do indeed form an inverse semigroup
![]() $S=\mathcal {S}(\pi )$
.
$S=\mathcal {S}(\pi )$
.
Certainly the diagonal
![]() $N=\mathcal {N}(\pi )$
is a subsemigroup. For any
$N=\mathcal {N}(\pi )$
is a subsemigroup. For any
![]() $a\in S$
and
$a\in S$
and
![]() $n\in N$
,
$n\in N$
,
as
![]() $\mathrm {dom}(n)\subseteq G^0$
and
$\mathrm {dom}(n)\subseteq G^0$
and
![]() $\mathrm {dom}(a)$
is a slice. Thus
$\mathrm {dom}(a)$
is a slice. Thus
![]() $an=ana^{-1}a\in Na$
, showing that
$an=ana^{-1}a\in Na$
, showing that
![]() $aN\subseteq Na$
, while the reverse inclusion follows by a dual argument, that is,
$aN\subseteq Na$
, while the reverse inclusion follows by a dual argument, that is,
![]() $aN=Na$
, showing that N is normal. As the only idempotents in a groupoid are units, the idempotent sections are precisely those whose range consists of units, that is,
$aN=Na$
, showing that N is normal. As the only idempotents in a groupoid are units, the idempotent sections are precisely those whose range consists of units, that is,
which is normal by Proposition 2.7. As units commute with isotropy elements of any groupoid, it follows that
![]() $nz=zn$
, for all
$nz=zn$
, for all
![]() $n\in N$
and
$n\in N$
and
![]() $z\in Z$
, that is,
$z\in Z$
, that is,
![]() $Z\subseteq \mathsf {Z}(N)$
.
$Z\subseteq \mathsf {Z}(N)$
.
Note here that N will be strictly bigger than
![]() $Z=\mathsf {E}(S)$
, as long as there are at least some slice-sections of
$Z=\mathsf {E}(S)$
, as long as there are at least some slice-sections of
![]() $\pi $
taking nonunit values. So in this case, the above structured semigroup is different from the canonical one mentioned after Definition 2.6 formed by simply taking
$\pi $
taking nonunit values. So in this case, the above structured semigroup is different from the canonical one mentioned after Definition 2.6 formed by simply taking
![]() $N=Z=\mathsf {E}(S)$
.
$N=Z=\mathsf {E}(S)$
.
We can also consider certain inverse subsemigroups of slice-sections.
Example 3.7. If G is an étale groupoid with Hausdorff unit space
![]() $G^0$
then pointwise products
$G^0$
then pointwise products
![]() $KL$
of compact subsets
$KL$
of compact subsets
![]() $K,L\subseteq G$
are again compact. If
$K,L\subseteq G$
are again compact. If
![]() $\pi :F\rightarrow G$
is a groupoid bundle then it follows that the slice-sections defined on (open) compact slices form an inverse subsemigroup
$\pi :F\rightarrow G$
is a groupoid bundle then it follows that the slice-sections defined on (open) compact slices form an inverse subsemigroup
![]() $S\subseteq \mathcal {S}(\pi )$
. Here it is natural to restrict to ample groupoids (where
$S\subseteq \mathcal {S}(\pi )$
. Here it is natural to restrict to ample groupoids (where
![]() $G^0$
and hence G has a basis of compact open subsets) so these compact-slice-sections can distinguish points of G.
$G^0$
and hence G has a basis of compact open subsets) so these compact-slice-sections can distinguish points of G.
If we have a trivial ample groupoid bundle
![]() $\pi :G\times (\mathbb {F}\setminus \{0\})\rightarrow G$
, where
$\pi :G\times (\mathbb {F}\setminus \{0\})\rightarrow G$
, where
![]() $\mathbb {F}$
is a discrete field, then any compact-slice-section s can be extended to the entirety of G with
$\mathbb {F}$
is a discrete field, then any compact-slice-section s can be extended to the entirety of G with
![]() $0$
values outside the original domain. The linear span of these then forms an algebra A of functions from G to
$0$
values outside the original domain. The linear span of these then forms an algebra A of functions from G to
![]() $\mathbb {F}$
commonly known as the ‘Steinberg algebra’ over G. The compact-slice-sections of nontrivial locally injective ample groupoid bundles
$\mathbb {F}$
commonly known as the ‘Steinberg algebra’ over G. The compact-slice-sections of nontrivial locally injective ample groupoid bundles
![]() $\pi :F\rightarrow G$
could thus be considered as ‘twisted Steinberg semigroups’.
$\pi :F\rightarrow G$
could thus be considered as ‘twisted Steinberg semigroups’.
Concrete (sub)semigroups of slice-sections arising in other contexts often only have ‘local inverses’.
Definition 3.8. Given a groupoid bundle
![]() $\pi :F\rightarrow G$
and semigroup
$\pi :F\rightarrow G$
and semigroup
![]() $S\subseteq \mathcal {S}(\pi )$
, let
$S\subseteq \mathcal {S}(\pi )$
, let
We call S a local-inverse semigroup if, for all
![]() $g\in G$
and
$g\in G$
and
![]() $a\in S_g$
, we have
$a\in S_g$
, we have
![]() $a'\in S_{g^{-1}}$
and
$a'\in S_{g^{-1}}$
and
![]() $b\in S_g$
with
$b\in S_g$
with
![]() $a'(h^{-1})=a(h)^{-1}$
, for all
$a'(h^{-1})=a(h)^{-1}$
, for all
![]() $h\in \mathrm {dom}(b)$
.
$h\in \mathrm {dom}(b)$
.
So the values of
![]() $a'$
above are the inverses of the values of a on some neighbourhood of g which is also the domain of some
$a'$
above are the inverses of the values of a on some neighbourhood of g which is also the domain of some
![]() $b\in S$
. In particular,
$b\in S$
. In particular,
![]() $\mathrm {dom}(b)\subseteq \mathrm {dom}(a)$
.
$\mathrm {dom}(b)\subseteq \mathrm {dom}(a)$
.
Example 3.9. As in [Reference Kumjian18], we can consider a Fell bundle
![]() $\pi :F\rightarrow G$
over a locally compact étale groupoid G with Hausdorff unit space
$\pi :F\rightarrow G$
over a locally compact étale groupoid G with Hausdorff unit space
![]() $G^0$
. This is not quite a groupoid bundle: even with line bundles, where the fibres are one-dimensional, each fibre still has a
$G^0$
. This is not quite a groupoid bundle: even with line bundles, where the fibres are one-dimensional, each fibre still has a
![]() $0$
. However, we can simply restrict
$0$
. However, we can simply restrict
![]() $\pi $
to the invertible elements
$\pi $
to the invertible elements
![]() $F^{\times }$
. The slice-sections a defined on open slices such that
$F^{\times }$
. The slice-sections a defined on open slices such that
![]() $\|a\|$
vanishes at infinity again form a subsemigroup
$\|a\|$
vanishes at infinity again form a subsemigroup
![]() $S\subseteq \mathcal {S}(\pi |_{F^{\times }})$
. Again we can extend any such slice-section to the entirety of G with
$S\subseteq \mathcal {S}(\pi |_{F^{\times }})$
. Again we can extend any such slice-section to the entirety of G with
![]() $0$
values outside the original domain. The linear span of these again forms an algebra, this time with a natural reduced algebra norm. Taking the completion then yields a C*-algebra A. Thus, S again forms a natural semigroup from which to generate A.
$0$
values outside the original domain. The linear span of these again forms an algebra, this time with a natural reduced algebra norm. Taking the completion then yields a C*-algebra A. Thus, S again forms a natural semigroup from which to generate A.
Note that the inverse of a function vanishing at infinity may not vanish at infinity and could even be unbounded, that is,
![]() $a\in S$
does not imply
$a\in S$
does not imply
![]() $a^{-1}\in S$
, so S is not an inverse semigroup. However, if
$a^{-1}\in S$
, so S is not an inverse semigroup. However, if
![]() $a\in S_g$
then we have an open neighbourhood
$a\in S_g$
then we have an open neighbourhood
![]() $O\subseteq \mathrm {dom}(a)$
of g on which
$O\subseteq \mathrm {dom}(a)$
of g on which
![]() $a^{-1}$
is bounded. We can then define a function
$a^{-1}$
is bounded. We can then define a function
![]() $a'\in S_{g^{-1}}$
which vanishes at infinity but coincides with
$a'\in S_{g^{-1}}$
which vanishes at infinity but coincides with
![]() $a^{-1}$
on
$a^{-1}$
on
![]() $O^{-1}$
. Taking any
$O^{-1}$
. Taking any
![]() $b\in S_g$
with
$b\in S_g$
with
![]() $\mathrm {dom}(b)\subseteq O$
then witnesses the fact that S is a local-inverse semigroup.
$\mathrm {dom}(b)\subseteq O$
then witnesses the fact that S is a local-inverse semigroup.
Similarly, the sections of
![]() $\pi $
with range in
$\pi $
with range in
![]() $F^0$
rarely vanish at infinity (only if their domain is also compact). Thus, it is more natural to allow scalar multiples of units as well, that is, instead of taking Z to be the idempotent slice-sections as in Proposition 3.6, we can take
$F^0$
rarely vanish at infinity (only if their domain is also compact). Thus, it is more natural to allow scalar multiples of units as well, that is, instead of taking Z to be the idempotent slice-sections as in Proposition 3.6, we can take
![]() $Z=S\cap \mathcal {Z}(\pi )$
, where
$Z=S\cap \mathcal {Z}(\pi )$
, where
![]() $\mathcal {Z}(\pi )$
denotes the central-diagonal
$\mathcal {Z}(\pi )$
denotes the central-diagonal
As the name suggests,
![]() $\mathcal {Z}(\pi )$
is a central subsemigroup of the diagonal
$\mathcal {Z}(\pi )$
is a central subsemigroup of the diagonal
![]() $\mathcal {N}(\pi )$
and hence
$\mathcal {N}(\pi )$
and hence
![]() $Z=S\cap \mathcal {Z}(\pi )$
is also a central subsemigroup of
$Z=S\cap \mathcal {Z}(\pi )$
is also a central subsemigroup of
![]() $N=S\cap \mathcal {N}(\pi )$
. Moreover, note that we can always choose the
$N=S\cap \mathcal {N}(\pi )$
. Moreover, note that we can always choose the
![]() $a'$
in the previous paragraph so that
$a'$
in the previous paragraph so that
![]() $aa',a'a\in Z$
. Also, unlike in the previous examples, N and Z here may not be normal (for example, in [Reference Bice and Clark4, Example 7.3] mentioned above) but they will still be binormal and hence
$aa',a'a\in Z$
. Also, unlike in the previous examples, N and Z here may not be normal (for example, in [Reference Bice and Clark4, Example 7.3] mentioned above) but they will still be binormal and hence
![]() $(S,N,Z)$
will still form a structured semigroup.
$(S,N,Z)$
will still form a structured semigroup.
Another possibility is to leave
![]() $\pi $
as is; even though F is only a category, not a groupoid, the slice-sections
$\pi $
as is; even though F is only a category, not a groupoid, the slice-sections
![]() $\mathcal {S}(\pi )$
still form a semigroup with a subsemigroup S of functions vanishing at infinity. Again taking
$\mathcal {S}(\pi )$
still form a semigroup with a subsemigroup S of functions vanishing at infinity. Again taking
![]() $N=S\cap \mathcal {N}(\pi )$
and
$N=S\cap \mathcal {N}(\pi )$
and
![]() $Z=S\cap \mathcal {Z}(\pi )$
, we see that N may not even be binormal now; however, it will still be Z-trinormal, that is,
$Z=S\cap \mathcal {Z}(\pi )$
, we see that N may not even be binormal now; however, it will still be Z-trinormal, that is,
![]() $(S,N,Z)$
will still form a structured semigroup.
$(S,N,Z)$
will still form a structured semigroup.
Our main goal is to obtain a kind of converse to Proposition 3.6. More precisely, we want to show how to represent a structured semigroup as a subsemigroup of
![]() $\mathcal {S}(\pi )$
, for some étale bundle
$\mathcal {S}(\pi )$
, for some étale bundle
![]() $\pi :F\rightarrow G$
, which is universal for an appropriate class of representations on even more general groupoid bundles.
$\pi :F\rightarrow G$
, which is universal for an appropriate class of representations on even more general groupoid bundles.
To get some hint as to how we might do this, take an étale bundle
![]() $\pi :F\rightarrow G$
and consider the inverse semigroup of all slice-sections
$\pi :F\rightarrow G$
and consider the inverse semigroup of all slice-sections
![]() $S=\mathcal {S}(\pi )$
. The sets of the form
$S=\mathcal {S}(\pi )$
. The sets of the form
![]() $S_g$
, for
$S_g$
, for
![]() $g\in G$
, form ‘cosets’ in an appropriate sense, generalising the usual cosets one considers in inverse semigroups; see (Coset) above. Indeed, these general cosets can still be defined via a domination relation
$g\in G$
, form ‘cosets’ in an appropriate sense, generalising the usual cosets one considers in inverse semigroups; see (Coset) above. Indeed, these general cosets can still be defined via a domination relation
![]() $<$
on S generalising the usual order on an inverse semigroup (basically
$<$
on S generalising the usual order on an inverse semigroup (basically
![]() $<$
corresponds to inclusion of domains; see Proposition 5.2 below). Moreover, for any
$<$
corresponds to inclusion of domains; see Proposition 5.2 below). Moreover, for any
![]() $g,h\in G$
such that
$g,h\in G$
such that
![]() $gh$
is defined, the products
$gh$
is defined, the products
![]() $S_gS_h$
of slice-sections in
$S_gS_h$
of slice-sections in
![]() $S_g$
and
$S_g$
and
![]() $S_h$
are
$S_h$
are
![]() $<$
-coinitial in the family of slice-sections
$<$
-coinitial in the family of slice-sections
![]() $S_{gh}$
. In this way, the product structure of S encodes that of G.
$S_{gh}$
. In this way, the product structure of S encodes that of G.
For each
![]() $f\in F$
and
$f\in F$
and
![]() $g\in G$
with
$g\in G$
with
![]() $\pi (f)=g$
, we can further consider the subfamily
$\pi (f)=g$
, we can further consider the subfamily
 $S^f\subseteq S_g$
of slice-sections taking the value f at g
$S^f\subseteq S_g$
of slice-sections taking the value f at g
These form equivalence classes in
![]() $S_g$
modulo a relation
$S_g$
modulo a relation
![]() $\sim _{S_g}$
again determined by the structured semigroup. Moreover, for any
$\sim _{S_g}$
again determined by the structured semigroup. Moreover, for any
![]() $e,f\in F$
such that
$e,f\in F$
such that
![]() $ef$
is defined,
$ef$
is defined,
![]() $S^{ef}$
coincides with the equivalence class containing
$S^{ef}$
coincides with the equivalence class containing
![]() $S^eS^f$
, again showing how the product structure of F is encoded by that of S.
$S^eS^f$
, again showing how the product structure of F is encoded by that of S.
The goal is thus to examine the domination relation
![]() $<$
in structured semigroups and the cosets and equivalence classes it gives rise to, in order to construct étale bundles on which to obtain universal slice-section representations. For universality, however, we first need to consider morphisms between groupoid bundles which correspond to semigroup homomorphisms of the associated slice-sections.
$<$
in structured semigroups and the cosets and equivalence classes it gives rise to, in order to construct étale bundles on which to obtain universal slice-section representations. For universality, however, we first need to consider morphisms between groupoid bundles which correspond to semigroup homomorphisms of the associated slice-sections.
4 Morphisms
Before considering groupoid bundles, we first need an appropriate notion of morphism for étale groupoids. One option would be to consider the (functional) étale morphisms from Section 2.2, which would be fine for Section 11 where we consider general cosets. However, when we restrict our attention to directed cosets in Section 12, we need more general (relational) Zakrzewski morphisms; see Theorem 12.14 below.
First let us consider any
![]() $\phi \subseteq G\times H$
as a relation ‘from H to G’, where
$\phi \subseteq G\times H$
as a relation ‘from H to G’, where
![]() $g\mathrel {\phi }h$
means
$g\mathrel {\phi }h$
means
![]() $(g,h)\in \phi $
. The flip of
$(g,h)\in \phi $
. The flip of
![]() $\phi $
is denoted by
$\phi $
is denoted by
![]() $\phi ^{-1}\subseteq H\times G$
, that is,
$\phi ^{-1}\subseteq H\times G$
, that is,
![]() $h\mathrel {\phi ^{-1}}g$
if and only if
$h\mathrel {\phi ^{-1}}g$
if and only if
![]() $g\mathrel {\phi }h$
. The image of
$g\mathrel {\phi }h$
. The image of
![]() $H'\subseteq H$
and preimage of
$H'\subseteq H$
and preimage of
![]() $G'\subseteq G$
are denoted by
$G'\subseteq G$
are denoted by
In particular, we define the domain and range of
![]() $\phi \subseteq G\times H$
by
$\phi \subseteq G\times H$
by
The composition of
![]() $\phi \subseteq G\times H$
and
$\phi \subseteq G\times H$
and
![]() $\psi \subseteq H\times I$
is the relation
$\psi \subseteq H\times I$
is the relation
![]() $\phi \circ \psi \subseteq G\times I$
where
$\phi \circ \psi \subseteq G\times I$
where
Definition 4.1. If G and H are groupoids,
![]() $\phi \subseteq G\times H$
is functorial if
$\phi \subseteq G\times H$
is functorial if
 $$ \begin{align*} g\mathrel{\phi}h\quad&\Rightarrow\quad g^{-1}\mathrel{\phi}h^{-1},\quad\text{and}\\ g\mathrel{\phi}h,\ g'\mathrel{\phi}h'\text{ and }\mathsf{s}(h)=\mathsf{r}(h')\quad&\Rightarrow\quad\mathsf{s}(g)=\mathsf{r}(g')\text{ and } gg'\mathrel{\phi}hh'. \end{align*} $$
$$ \begin{align*} g\mathrel{\phi}h\quad&\Rightarrow\quad g^{-1}\mathrel{\phi}h^{-1},\quad\text{and}\\ g\mathrel{\phi}h,\ g'\mathrel{\phi}h'\text{ and }\mathsf{s}(h)=\mathsf{r}(h')\quad&\Rightarrow\quad\mathsf{s}(g)=\mathsf{r}(g')\text{ and } gg'\mathrel{\phi}hh'. \end{align*} $$
In particular, note that
![]() $\mathrm {dom}(\phi )$
is a subgroupoid when
$\mathrm {dom}(\phi )$
is a subgroupoid when
![]() $\phi $
is functorial.
$\phi $
is functorial.
As usual, we call
![]() $\phi \subseteq G\times H$
a function when the image
$\phi \subseteq G\times H$
a function when the image
![]() $\phi \{h\}=\phi [\{h\}]$
of every singleton h in
$\phi \{h\}=\phi [\{h\}]$
of every singleton h in
![]() $\mathrm {dom}(\phi )$
is again a singleton in
$\mathrm {dom}(\phi )$
is again a singleton in
![]() $\mathrm {ran}(\phi )$
, in which case
$\mathrm {ran}(\phi )$
, in which case
So a functorial function
![]() $\phi \subseteq G\times H$
is just a functor on
$\phi \subseteq G\times H$
is just a functor on
![]() $\mathrm {dom}(\phi )$
in the usual sense. We also get functions when we restrict functorial relations to slices in the range.
$\mathrm {dom}(\phi )$
in the usual sense. We also get functions when we restrict functorial relations to slices in the range.
Proposition 4.2. If
![]() $\phi \subseteq G\times H$
is functorial then
$\phi \subseteq G\times H$
is functorial then
Proof. It suffices to show that
To see this, note that
![]() $f,g\mathrel {\phi }h$
implies
$f,g\mathrel {\phi }h$
implies
![]() $g^{-1}\mathrel {\phi }h^{-1}$
by functoriality. As
$g^{-1}\mathrel {\phi }h^{-1}$
by functoriality. As
![]() $\mathsf {s}(h)=\mathsf {r}(h^{-1})$
, functoriality again yields
$\mathsf {s}(h)=\mathsf {r}(h^{-1})$
, functoriality again yields
![]() $\mathsf {s}(f)=\mathsf {r}(g^{-1})=\mathsf {s}(g)$
.
$\mathsf {s}(f)=\mathsf {r}(g^{-1})=\mathsf {s}(g)$
.
We extend the terminology in [Reference Brown7, Reference Higgins15] from functions to relations.
Definition 4.3. Assume that G and H are groupoids and
![]() $\phi \subseteq G\times H$
is functorial. We call
$\phi \subseteq G\times H$
is functorial. We call
![]() $\phi $
star-injective (surjective, bijective) if, whenever
$\phi $
star-injective (surjective, bijective) if, whenever
![]() $h\in H$
and
$h\in H$
and
![]() $\mathsf {r}(g)\mathrel {\phi }h\in H^0$
, there is at most (at least, precisely) one
$\mathsf {r}(g)\mathrel {\phi }h\in H^0$
, there is at most (at least, precisely) one
![]() $i\in H$
such that
$i\in H$
such that
![]() $\mathsf {r}(i)=h$
and
$\mathsf {r}(i)=h$
and
![]() $g\mathrel {\phi }i$
.
$g\mathrel {\phi }i$
.
More symbolically, these definitions can be summarised as follows:
These have several equivalent characterisations; for example,
![]() $\phi $
is star-injective if and only if its kernel is discrete, that is, unit-preimages are units. More important for us is the fact that star-injectivity means
$\phi $
is star-injective if and only if its kernel is discrete, that is, unit-preimages are units. More important for us is the fact that star-injectivity means
![]() $\phi ^{-1}$
respects slices.
$\phi ^{-1}$
respects slices.
Proposition 4.4. The functorial
![]() $\phi \subseteq G\times H$
is star-injective precisely when
$\phi \subseteq G\times H$
is star-injective precisely when
![]() $\phi ^{-1}[G^0]\subseteq H^0$
or, equivalently, when
$\phi ^{-1}[G^0]\subseteq H^0$
or, equivalently, when
Proof. If
![]() $\phi $
is not star-injective then we have
$\phi $
is not star-injective then we have
![]() $h\in H^0$
and distinct
$h\in H^0$
and distinct
![]() $i,j\in H$
with
$i,j\in H$
with
![]() $\mathsf {r}(h)=\mathsf {r}(i)=h$
and
$\mathsf {r}(h)=\mathsf {r}(i)=h$
and
![]() $g\mathrel {\phi }i,j$
. Then
$g\mathrel {\phi }i,j$
. Then
![]() $G^0\ni \mathsf {s}(g)=g^{-1}g\mathrel {\phi }i^{-1}j\notin H^0$
by functoriality.
$G^0\ni \mathsf {s}(g)=g^{-1}g\mathrel {\phi }i^{-1}j\notin H^0$
by functoriality.
Conversely, if we have
![]() $G^0\ni g\mathrel {\phi }h\notin H^0$
then
$G^0\ni g\mathrel {\phi }h\notin H^0$
then
![]() $g=\mathsf {r}(g)\mathrel {\phi }\mathsf {r}(h)\neq h$
, even though
$g=\mathsf {r}(g)\mathrel {\phi }\mathsf {r}(h)\neq h$
, even though
![]() $\mathsf {r}(\mathsf {r}(h))=\mathsf {r}(h)$
, showing that
$\mathsf {r}(\mathsf {r}(h))=\mathsf {r}(h)$
, showing that
![]() $\phi $
is not star-injective.
$\phi $
is not star-injective.
Now if
![]() $\phi ^{-1}[G^0]\subseteq H^0$
then, for any slice
$\phi ^{-1}[G^0]\subseteq H^0$
then, for any slice
![]() $B\subseteq G^0$
, functoriality yields
$B\subseteq G^0$
, functoriality yields
Likewise,
![]() $(\phi ^{-1}[B])^{-1}\phi ^{-1}[B]\subseteq H^0$
, showing that
$(\phi ^{-1}[B])^{-1}\phi ^{-1}[B]\subseteq H^0$
, showing that
![]() $\phi ^{-1}[B]$
is a slice.
$\phi ^{-1}[B]$
is a slice.
Conversely, if
![]() $\phi ^{-1}\{g\}$
is a slice then, in particular,
$\phi ^{-1}\{g\}$
is a slice then, in particular,
![]() $i,j\in \phi ^{-1}\{g\}\cap \mathsf {r}^{-1}\{h\}$
implies
$i,j\in \phi ^{-1}\{g\}\cap \mathsf {r}^{-1}\{h\}$
implies
![]() $i=j$
. So if this holds for all
$i=j$
. So if this holds for all
![]() $g\in G$
then
$g\in G$
then
![]() $\phi $
is star-injective.
$\phi $
is star-injective.
On the other hand, star-surjectivity means
![]() $\phi ^{-1}$
respects products.
$\phi ^{-1}$
respects products.
Proposition 4.5. The functorial
![]() $\phi \subseteq G\times H$
is star-surjective if and only if, for all
$\phi \subseteq G\times H$
is star-surjective if and only if, for all
![]() $A,B\subseteq ~G$
,
$A,B\subseteq ~G$
,
Proof. Assume that
![]() $\phi \subseteq G\times H$
is functorial and star-surjective. If
$\phi \subseteq G\times H$
is functorial and star-surjective. If
![]() $A,B\subseteq G$
then
$A,B\subseteq G$
then
![]() $\phi ^{-1}[A]\phi ^{-1}[B]\subseteq \phi ^{-1}[AB]$
by the functoriality of
$\phi ^{-1}[A]\phi ^{-1}[B]\subseteq \phi ^{-1}[AB]$
by the functoriality of
![]() $\phi $
. Conversely, take
$\phi $
. Conversely, take
![]() $a\in A$
,
$a\in A$
,
![]() $b\in B$
and
$b\in B$
and
![]() $h\in H$
with
$h\in H$
with
![]() $ab\mathrel {\phi }h$
. By functoriality,
$ab\mathrel {\phi }h$
. By functoriality,
![]() $\mathsf {r}(a)=\mathsf {r}(ab)\mathrel {\phi }\mathsf {r}(h)$
. Star-surjectivity then yields
$\mathsf {r}(a)=\mathsf {r}(ab)\mathrel {\phi }\mathsf {r}(h)$
. Star-surjectivity then yields
![]() $i\in \phi ^{-1}\{a\}$
with
$i\in \phi ^{-1}\{a\}$
with
![]() $\mathsf {r}(h)=\mathsf {r}(i)$
. Again functoriality yields
$\mathsf {r}(h)=\mathsf {r}(i)$
. Again functoriality yields
![]() $b=a^{-1}(ab)\mathrel {\phi }i^{-1}h$
and hence
$b=a^{-1}(ab)\mathrel {\phi }i^{-1}h$
and hence
![]() $h=i(i^{-1}h)\in \phi ^{-1}[A]\phi ^{-1}[B]$
, showing that
$h=i(i^{-1}h)\in \phi ^{-1}[A]\phi ^{-1}[B]$
, showing that
![]() $\phi ^{-1}[AB]\subseteq \phi ^{-1}[A]\phi ^{-1}[B]$
too.
$\phi ^{-1}[AB]\subseteq \phi ^{-1}[A]\phi ^{-1}[B]$
too.
On the other hand, if (4-3) holds and
![]() $\mathsf {r}(g)\mathrel {\phi }h\in H^0$
then
$\mathsf {r}(g)\mathrel {\phi }h\in H^0$
then
Thus, we have
![]() $i\in \phi ^{-1}\{g\}$
and
$i\in \phi ^{-1}\{g\}$
and
![]() $j\in \phi ^{-1}\{g^{-1}\}$
with
$j\in \phi ^{-1}\{g^{-1}\}$
with
![]() $h=ij$
. As
$h=ij$
. As
![]() $h\in H^0$
, this means that
$h\in H^0$
, this means that
![]() $h=\mathsf {r}(h)=\mathsf {r}(ij)=\mathsf {r}(i)$
, showing that
$h=\mathsf {r}(h)=\mathsf {r}(ij)=\mathsf {r}(i)$
, showing that
![]() $\phi $
is star-surjective.
$\phi $
is star-surjective.
In fact, the proofs show that it suffices to consider singleton A and B in (4-2) and (4-3). We also note that
![]() $\phi $
is star-surjective if and only if
$\phi $
is star-surjective if and only if
![]() $\mathrm {ran}(\phi )$
is an ideal of G; see (Ideal) below.
$\mathrm {ran}(\phi )$
is an ideal of G; see (Ideal) below.
Extending the usual notion for functions, when G and H are topological spaces and
![]() $\phi \subseteq G\times H$
, we call
$\phi \subseteq G\times H$
, we call
![]() $\phi $
continuous if
$\phi $
continuous if
![]() $\phi ^{-1}[O]$
is open, for all open
$\phi ^{-1}[O]$
is open, for all open
![]() $O\subseteq G$
.
$O\subseteq G$
.
Definition 4.6. A Zakrzewski morphism
![]() $\phi \subseteq G\times H$
between étale groupoids G and H is a continuous star-bijective functorial relation.
$\phi \subseteq G\times H$
between étale groupoids G and H is a continuous star-bijective functorial relation.
The idea of considering relational morphisms between groupoids comes from [Reference Zakrzewski35] and was further studied in [Reference Stachura30]. As in Section 2.2, a functional Zakrzewski morphism will be called an étale morphism.
Remark 4.7. Zakrzewski morphisms include both continuous functions and group homomorphisms but in opposite directions. Indeed, if G and H are étale groupoids with
![]() $G=G^0$
and
$G=G^0$
and
![]() $H=H^0$
, that is, if G and H are just topological spaces under the trivial product defined on the diagonal, a Zakrzewski morphism
$H=H^0$
, that is, if G and H are just topological spaces under the trivial product defined on the diagonal, a Zakrzewski morphism
![]() $\phi \subseteq G\times H$
is just a continuous function from an open subset of H to G. At the other extreme, if
$\phi \subseteq G\times H$
is just a continuous function from an open subset of H to G. At the other extreme, if
![]() $G^0$
and
$G^0$
and
![]() $H^0$
are singletons, that is, if G and H are discrete groups, then nonempty
$H^0$
are singletons, that is, if G and H are discrete groups, then nonempty
![]() $\phi \subseteq G\times H$
is a Zakrzewski morphism if and only if
$\phi \subseteq G\times H$
is a Zakrzewski morphism if and only if
![]() $\phi ^{-1}\subseteq H\times G$
is a group homomorphism from G to H.
$\phi ^{-1}\subseteq H\times G$
is a group homomorphism from G to H.
Zakrzewski morphisms can also be seen as generalisations of groupoid bundles. Indeed, if F and G are étale groupoids then a function
![]() $\pi :F\rightarrow G$
is a groupoid bundle if and only if
$\pi :F\rightarrow G$
is a groupoid bundle if and only if
![]() $\pi ^{-1}\subseteq F\times G$
is an open Zakrzewski morphism, that is, a Zakrzewski morphism such that
$\pi ^{-1}\subseteq F\times G$
is an open Zakrzewski morphism, that is, a Zakrzewski morphism such that
![]() $\pi ^{-1}[O]$
is open, for all open
$\pi ^{-1}[O]$
is open, for all open
![]() $O\subseteq G$
.
$O\subseteq G$
.
Now suppose we have a groupoid bundle
![]() $\pi :F\rightarrow G$
and a Zakrzewski morphism
$\pi :F\rightarrow G$
and a Zakrzewski morphism
![]() $\phi \subseteq G\times H$
. Consider the subspace of
$\phi \subseteq G\times H$
. Consider the subspace of
![]() $F\times H$
given by
$F\times H$
given by
Note that
![]() $\phi ^{\pi } F$
is a topological groupoid under the product
$\phi ^{\pi } F$
is a topological groupoid under the product
Let
![]() $\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
denote the projection onto H, that is,
$\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
denote the projection onto H, that is,
![]() $\pi _{\phi }(f,h)=h$
.
$\pi _{\phi }(f,h)=h$
.
Proposition 4.8. If
![]() $\pi :F\rightarrow G$
is a groupoid bundle and
$\pi :F\rightarrow G$
is a groupoid bundle and
![]() $\phi \subseteq G\times H$
is a Zakrzewski morphism then
$\phi \subseteq G\times H$
is a Zakrzewski morphism then
![]() $\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
is also a groupoid bundle.
$\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
is also a groupoid bundle.
Proof. The definition of the topology and product on
![]() $\phi ^{\pi } F$
ensures that
$\phi ^{\pi } F$
ensures that
![]() $\pi _{\phi }$
is a continuous isocofibration. It only remains to show that
$\pi _{\phi }$
is a continuous isocofibration. It only remains to show that
![]() $\pi _{\phi }$
is also an open map. To see this, take open
$\pi _{\phi }$
is also an open map. To see this, take open
![]() $O\subseteq F$
and
$O\subseteq F$
and
![]() $N\subseteq H$
and note that
$N\subseteq H$
and note that
 $$ \begin{align*} \pi_{\phi}[(O\times N)\cap\phi^{\pi} F]&=\{h\in N:\text{ there exists } f\in O\ (\pi(f)\mathrel{\phi}h)\}\\ &=N\cap\phi^{-1}[\pi[O]], \end{align*} $$
$$ \begin{align*} \pi_{\phi}[(O\times N)\cap\phi^{\pi} F]&=\{h\in N:\text{ there exists } f\in O\ (\pi(f)\mathrel{\phi}h)\}\\ &=N\cap\phi^{-1}[\pi[O]], \end{align*} $$
which is open because
![]() $\phi $
is continuous and
$\phi $
is continuous and
![]() $\pi $
is an open map.
$\pi $
is an open map.
This
![]() $\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
is the pullback bundle of
$\pi _{\phi }:\phi ^{\pi } F\rightarrow H$
is the pullback bundle of
![]() $\pi $
induced by
$\pi $
induced by
![]() $\phi $
.
$\phi $
.
Definition 4.9. Let
![]() $\pi :F\rightarrow G$
and
$\pi :F\rightarrow G$
and
![]() $\pi ':F'\rightarrow G'$
be groupoid bundles. If
$\pi ':F'\rightarrow G'$
be groupoid bundles. If
(1)
 $\phi \subseteq G\times G'$
is a Zakrzewski morphism,
$\phi \subseteq G\times G'$
is a Zakrzewski morphism,(2)
 $\tau :\phi ^{\pi } F\rightarrow F'$
is a continuous functor and
$\tau :\phi ^{\pi } F\rightarrow F'$
is a continuous functor and(3)
 $\pi _{\phi }=\pi '\circ \tau $
(that is,
$\pi _{\phi }=\pi '\circ \tau $
(that is,
 $\pi '(\tau (f,g'))=g'$
, for all
$\pi '(\tau (f,g'))=g'$
, for all
 $(f,g')\in \phi ^{\pi } F$
)
$(f,g')\in \phi ^{\pi } F$
)
then we call the pair
![]() $(\phi ,\tau )$
a Zakrzewski–Pierce morphism from
$(\phi ,\tau )$
a Zakrzewski–Pierce morphism from
![]() $\pi $
to
$\pi $
to
![]() $\pi '$
. If
$\pi '$
. If
![]() $\phi $
is also a function then
$\phi $
is also a function then
![]() $(\phi ,\tau )$
is a Pierce morphism.
$(\phi ,\tau )$
is a Pierce morphism.
Similar morphisms for ring bundles are considered in [Reference Pierce25, Definition 6.1], hence the name (for analogous C*-bundle morphisms, see [Reference Varela33, Definition 4.3]). Like in [Reference Pierce25, Lemma 6.2], Zakrzewski–Pierce morphisms of groupoid bundles naturally yield semigroup homomorphisms of their slice-sections.
Theorem 4.10. If
![]() $(\phi ,\tau )$
is a Zakrzewski–Pierce morphism from
$(\phi ,\tau )$
is a Zakrzewski–Pierce morphism from
![]() $\pi :F\rightarrow G$
to
$\pi :F\rightarrow G$
to
![]() $\pi ':F'\rightarrow G'$
, we have a semigroup homomorphism
$\pi ':F'\rightarrow G'$
, we have a semigroup homomorphism
![]() ${\tau }/{\phi }:\mathcal {S}(\pi )\rightarrow \mathcal {S}(\pi ')$
given by
${\tau }/{\phi }:\mathcal {S}(\pi )\rightarrow \mathcal {S}(\pi ')$
given by
 $$ \begin{align*} \frac{\tau}{\phi}(a)=\tau\circ(((a\circ\phi)\times\mathrm{id})\circ\delta), \end{align*} $$
$$ \begin{align*} \frac{\tau}{\phi}(a)=\tau\circ(((a\circ\phi)\times\mathrm{id})\circ\delta), \end{align*} $$
where
![]() $\delta (g')=(g',g')$
and
$\delta (g')=(g',g')$
and
![]() $\mathrm {id}(g')=g'$
.
$\mathrm {id}(g')=g'$
.
Proof. Assume that a is a slice-section of
![]() $\pi $
. In particular,
$\pi $
. In particular,
![]() $\mathrm {dom}(a)$
is an open slice, as is
$\mathrm {dom}(a)$
is an open slice, as is
 $$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\bigg)=\mathrm{dom}(a\circ\phi)=\phi^{-1}[\mathrm{dom}(a)], \end{align*} $$
$$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\bigg)=\mathrm{dom}(a\circ\phi)=\phi^{-1}[\mathrm{dom}(a)], \end{align*} $$
because
![]() $\phi $
is continuous and star-injective; see (4-2). As a and
$\phi $
is continuous and star-injective; see (4-2). As a and
![]() $\tau $
are also continuous, so is
$\tau $
are also continuous, so is
![]() $({\tau }/{\phi })(a)$
. Moreover,
$({\tau }/{\phi })(a)$
. Moreover,
![]() $\phi \cap (\mathrm {dom}(a)\times G')$
and hence
$\phi \cap (\mathrm {dom}(a)\times G')$
and hence
![]() $a\circ \phi $
is function, by (4-1). Thus,
$a\circ \phi $
is function, by (4-1). Thus,
![]() $({\tau }/{\phi })(a)$
is a function too such that, for all
$({\tau }/{\phi })(a)$
is a function too such that, for all
![]() $g'\in \mathrm {dom}(({\tau }/{\phi })(a))$
,
$g'\in \mathrm {dom}(({\tau }/{\phi })(a))$
,
 $$ \begin{align*} \frac{\tau}{\phi}(a)(g')=\tau((a\circ\phi)(g'),g') \end{align*} $$
$$ \begin{align*} \frac{\tau}{\phi}(a)(g')=\tau((a\circ\phi)(g'),g') \end{align*} $$
(which is defined because
![]() $((a\circ \phi )(g'),g')\in \phi ^{\pi }$
, as a is a section of
$((a\circ \phi )(g'),g')\in \phi ^{\pi }$
, as a is a section of
![]() $\pi $
). It follows that
$\pi $
). It follows that
![]() $\pi '(({\tau }/{\phi })(a)(g'))=\pi '(\tau ((a\circ \phi )(g'),g'))=\pi _{\phi }((a\circ \phi )(g'),g')=g'$
. This all shows that
$\pi '(({\tau }/{\phi })(a)(g'))=\pi '(\tau ((a\circ \phi )(g'),g'))=\pi _{\phi }((a\circ \phi )(g'),g')=g'$
. This all shows that
![]() $({\tau }/{\phi })(a)$
is a slice-section of
$({\tau }/{\phi })(a)$
is a slice-section of
![]() $\pi '$
, that is,
$\pi '$
, that is,
![]() $({\tau }/{\phi })(a)\in \mathcal {S}(\pi ')$
.
$({\tau }/{\phi })(a)\in \mathcal {S}(\pi ')$
.
Now, given another slice-section
![]() $b\in \mathcal {S}(\pi )$
, note that
$b\in \mathcal {S}(\pi )$
, note that
 $$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(ab)\bigg)&=\phi^{-1}[\mathrm{dom}(ab)]=\phi^{-1}[\mathrm{dom}(a)\mathrm{dom}(b)],\quad\text{and}\\ \mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\frac{\tau}{\phi}(b)\bigg)&=\mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\bigg)\mathrm{dom}\bigg(\frac{\tau}{\phi}(b)\bigg)=\phi^{-1}[\mathrm{dom}(a)]\phi^{-1}[\mathrm{dom}(b)], \end{align*} $$
$$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(ab)\bigg)&=\phi^{-1}[\mathrm{dom}(ab)]=\phi^{-1}[\mathrm{dom}(a)\mathrm{dom}(b)],\quad\text{and}\\ \mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\frac{\tau}{\phi}(b)\bigg)&=\mathrm{dom}\bigg(\frac{\tau}{\phi}(a)\bigg)\mathrm{dom}\bigg(\frac{\tau}{\phi}(b)\bigg)=\phi^{-1}[\mathrm{dom}(a)]\phi^{-1}[\mathrm{dom}(b)], \end{align*} $$
so
![]() $\mathrm {dom}(({\tau }/{\phi })(ab))=\mathrm {dom}(({\tau }/{\phi })(a)({\tau }/{\phi })(b))$
, by the star-surjectivity of
$\mathrm {dom}(({\tau }/{\phi })(ab))=\mathrm {dom}(({\tau }/{\phi })(a)({\tau }/{\phi })(b))$
, by the star-surjectivity of
![]() $\phi $
. Moreover, for any
$\phi $
. Moreover, for any
![]() $g'\in \mathrm {dom}(({\tau }/{\phi })(a))$
and
$g'\in \mathrm {dom}(({\tau }/{\phi })(a))$
and
![]() $h'\in \mathrm {dom}(({\tau }/{\phi })(b))$
such that
$h'\in \mathrm {dom}(({\tau }/{\phi })(b))$
such that
![]() $g'h'$
is defined, note that
$g'h'$
is defined, note that
 $$ \begin{align*} \frac{\tau}{\phi}(ab)(g'h')&=\tau((ab\circ\phi)(g'h'),g'h')\\ &=\tau((a\circ\phi)(g')(b\circ\phi)(h'),g'h')\\ &=\tau(((a\circ\phi)(g'),g')((b\circ\phi)(h'),h'))\\ &=\tau((a\circ\phi)(g'),g')\tau((b\circ\phi)(h'),h')\\ &=\frac{\tau}{\phi}(a)(g')\frac{\tau}{\phi}(b)(h')\\ &=\bigg(\frac{\tau}{\phi}(a)\frac{\tau}{\phi}(b)\bigg)(g'h'). \end{align*} $$
$$ \begin{align*} \frac{\tau}{\phi}(ab)(g'h')&=\tau((ab\circ\phi)(g'h'),g'h')\\ &=\tau((a\circ\phi)(g')(b\circ\phi)(h'),g'h')\\ &=\tau(((a\circ\phi)(g'),g')((b\circ\phi)(h'),h'))\\ &=\tau((a\circ\phi)(g'),g')\tau((b\circ\phi)(h'),h')\\ &=\frac{\tau}{\phi}(a)(g')\frac{\tau}{\phi}(b)(h')\\ &=\bigg(\frac{\tau}{\phi}(a)\frac{\tau}{\phi}(b)\bigg)(g'h'). \end{align*} $$
This shows that
![]() $({\tau }/{\phi })(ab)=({\tau }/{\phi })(a)({\tau }/{\phi })(b)$
, that is,
$({\tau }/{\phi })(ab)=({\tau }/{\phi })(a)({\tau }/{\phi })(b)$
, that is,
![]() $({\tau }/{\phi })$
is semigroup homo- morphism.
$({\tau }/{\phi })$
is semigroup homo- morphism.
5 Domination
We now make the following standing assumption throughout.
Definition 5.1. We define relations on S as follows:
 $$ \begin{align*} a<_sb\quad&\Leftrightarrow\quad asb=a=bsa,\ as,sa\in N\quad\text{and}\quad bs,sb\in Z;\\ a<b\quad&\Leftrightarrow\quad\text{there exists } s\in S\ (a<_sb). \end{align*} $$
$$ \begin{align*} a<_sb\quad&\Leftrightarrow\quad asb=a=bsa,\ as,sa\in N\quad\text{and}\quad bs,sb\in Z;\\ a<b\quad&\Leftrightarrow\quad\text{there exists } s\in S\ (a<_sb). \end{align*} $$
When
![]() $a<_sb$
, we say that b dominates a via s.
$a<_sb$
, we say that b dominates a via s.
To get some intuition for domination, we imagine that S is a subsemigroup of the slice-sections
![]() $\mathcal {S}(\pi )$
of some groupoid bundle
$\mathcal {S}(\pi )$
of some groupoid bundle
![]() $\pi :F\rightarrow G$
. As long as N lies in the diagonal
$\pi :F\rightarrow G$
. As long as N lies in the diagonal
![]() $\mathcal {N}(\pi )$
,
$\mathcal {N}(\pi )$
,
![]() $a<_sb$
means that s is an inverse of b on the domain of a.
$a<_sb$
means that s is an inverse of b on the domain of a.
Proposition 5.2. If
![]() $\pi :F\rightarrow G$
is a groupoid bundle and
$\pi :F\rightarrow G$
is a groupoid bundle and
![]() $a,s,b\in \mathcal {S}(\pi )$
,
$a,s,b\in \mathcal {S}(\pi )$
,
![]() $($
implicit in
$($
implicit in
![]() $s(g^{-1})=b(g)^{-1}$
is that
$s(g^{-1})=b(g)^{-1}$
is that
![]() $g^{-1}\in \mathrm {dom}(s)$
and
$g^{-1}\in \mathrm {dom}(s)$
and
![]() $g\in \mathrm {dom}(b))$
.
$g\in \mathrm {dom}(b))$
.
Proof. If
![]() $a=asb$
and
$a=asb$
and
![]() $g\in \mathrm {dom}(a)$
then
$g\in \mathrm {dom}(a)$
then
![]() $a(g)=asb(g)=a(h)s(i)b(j)$
, for some
$a(g)=asb(g)=a(h)s(i)b(j)$
, for some
![]() $h,i,j\in G$
with
$h,i,j\in G$
with
![]() $g=hij$
. Thus,
$g=hij$
. Thus,
![]() $\mathsf {r}(g)=\mathsf {r}(hij)=\mathsf {r}(h)$
so
$\mathsf {r}(g)=\mathsf {r}(hij)=\mathsf {r}(h)$
so
![]() $g=h$
, as
$g=h$
, as
![]() $\mathrm {dom}(a)$
is a slice. If
$\mathrm {dom}(a)$
is a slice. If
![]() $as\in \mathcal {N}(\pi )$
too then
$as\in \mathcal {N}(\pi )$
too then
![]() $gi=hi\in \mathrm {dom}(as)\subseteq G^0$
and hence
$gi=hi\in \mathrm {dom}(as)\subseteq G^0$
and hence
![]() $i=g^{-1}$
. Thus,
$i=g^{-1}$
. Thus,
![]() $g=hij=gg^{-1}j=j$
so
$g=hij=gg^{-1}j=j$
so
![]() $a(g)=a(g)s(g^{-1})b(g)$
and hence
$a(g)=a(g)s(g^{-1})b(g)$
and hence
![]() $s(g^{-1})b(g)\in F^0$
, that is,
$s(g^{-1})b(g)\in F^0$
, that is,
![]() $s(g^{-1})=b(g)^{-1}$
. This proves
$s(g^{-1})=b(g)^{-1}$
. This proves
![]() $\Rightarrow $
.
$\Rightarrow $
.
Now suppose that
![]() $s(g^{-1})=b(g)^{-1}$
, for all
$s(g^{-1})=b(g)^{-1}$
, for all
![]() $g\in \mathrm {dom}(a)$
. In particular,
$g\in \mathrm {dom}(a)$
. In particular,
![]() $\mathrm {dom}(a)\subseteq \mathrm {dom}(s)^{-1}$
and hence
$\mathrm {dom}(a)\subseteq \mathrm {dom}(s)^{-1}$
and hence
![]() $\mathrm {dom}(as)=\mathrm {dom}(a)\mathrm {dom}(s)\subseteq \mathrm {dom}(s)^{-1}\mathrm {dom}(s)\subseteq G^0$
so
$\mathrm {dom}(as)=\mathrm {dom}(a)\mathrm {dom}(s)\subseteq \mathrm {dom}(s)^{-1}\mathrm {dom}(s)\subseteq G^0$
so
![]() $as\in \mathcal {N}(\pi )$
. Also
$as\in \mathcal {N}(\pi )$
. Also
for all
![]() $g\in \mathrm {dom}(a)$
. In particular,
$g\in \mathrm {dom}(a)$
. In particular,
![]() $\mathsf {s}[\mathrm {dom}(a)]\subseteq \mathrm {dom}(sb)$
and hence
$\mathsf {s}[\mathrm {dom}(a)]\subseteq \mathrm {dom}(sb)$
and hence
which, together with the above computation, yields
![]() $a=asb$
, proving
$a=asb$
, proving
![]() $\Leftarrow $
.
$\Leftarrow $
.
In particular, if
![]() $\pi :F\rightarrow G$
is a groupoid bundle and
$\pi :F\rightarrow G$
is a groupoid bundle and
![]() $(S,N,Z)$
is a structured semigroup with
$(S,N,Z)$
is a structured semigroup with
![]() $S\subseteq \mathcal {S}(\pi )$
and
$S\subseteq \mathcal {S}(\pi )$
and
![]() $N\subseteq \mathcal {N}(\pi )$
then it follows from the above that
$N\subseteq \mathcal {N}(\pi )$
then it follows from the above that
On the other hand, if
![]() $S=\mathcal {S}(\pi )$
,
$S=\mathcal {S}(\pi )$
,
![]() $\mathcal {N}(\pi )\subseteq N$
and
$\mathcal {N}(\pi )\subseteq N$
and
![]() $\mathsf {E}(S)\subseteq Z$
then the converse holds. If we instead consider functions vanishing at infinity as in Example 3.9 then
$\mathsf {E}(S)\subseteq Z$
then the converse holds. If we instead consider functions vanishing at infinity as in Example 3.9 then
![]() $<$
is instead equivalent to compact containment
$<$
is instead equivalent to compact containment
![]() $\Subset $
of domains, that is,
$\Subset $
of domains, that is,
![]() $a<b$
means
$a<b$
means
![]() $\mathrm {dom}(a)\subseteq K\subseteq \mathrm {dom}(b)$
, for some compact
$\mathrm {dom}(a)\subseteq K\subseteq \mathrm {dom}(b)$
, for some compact
![]() $K\subseteq G$
(see [Reference Bice and Clark4, Proposition 4.4]).
$K\subseteq G$
(see [Reference Bice and Clark4, Proposition 4.4]).
On inverse semigroups,
![]() $<$
is just the usual ordering.
$<$
is just the usual ordering.
Proposition 5.3. If S is an inverse semigroup and
![]() $N=Z=\mathsf {E}(S)$
then
$N=Z=\mathsf {E}(S)$
then
Proof. If
![]() $a<b$
then we have
$a<b$
then we have
![]() $s\in S$
with
$s\in S$
with
![]() $a=asb\in Nb$
. Conversely, if
$a=asb\in Nb$
. Conversely, if
![]() $a=nb$
, for some
$a=nb$
, for some
![]() $n\in N$
, then
$n\in N$
, then
![]() $ab^{-1}=nbb^{-1}\in N$
and
$ab^{-1}=nbb^{-1}\in N$
and
![]() $ab^{-1}b=nbb^{-1}b=nb=a$
. Likewise
$ab^{-1}b=nbb^{-1}b=nb=a$
. Likewise
![]() $b^{-1}a=b^{-1}nb\in N$
and
$b^{-1}a=b^{-1}nb\in N$
and
![]() $bb^{-1}a=bb^{-1}nb=nbb^{-1}b=nb=a$
. As
$bb^{-1}a=bb^{-1}nb=nbb^{-1}b=nb=a$
. As
![]() $bb^{-1},b^{-1}b\in N$
, this shows that
$bb^{-1},b^{-1}b\in N$
, this shows that
![]() $a<_{b^{-1}}b$
.
$a<_{b^{-1}}b$
.
Our primary goal in this section is to show that the domination relation
![]() $<$
on general structured semigroups still has many of the same properties as the usual order relation on inverse semigroups.
$<$
on general structured semigroups still has many of the same properties as the usual order relation on inverse semigroups.
First we note that
![]() $<$
could have been defined in a more one-sided way. Note that here and elsewhere we make use of the fact that a result proved from S immediately yields a dual result for the opposite semigroup
$<$
could have been defined in a more one-sided way. Note that here and elsewhere we make use of the fact that a result proved from S immediately yields a dual result for the opposite semigroup
![]() $S^{\mathrm {op}}$
(where
$S^{\mathrm {op}}$
(where
![]() $a\cdot ^{\mathrm {op}}b=ba$
).
$a\cdot ^{\mathrm {op}}b=ba$
).
Proposition 5.4. For any
![]() $a,b,b'\in S$
,
$a,b,b'\in S$
,
 $$ \begin{align*} a<_sb\quad&\Leftrightarrow\quad asb=a,\ as\in N\quad\text{and}\quad bs,sb\in Z,\\ &\Leftrightarrow\quad bsa=a,\ sa\in N\quad\text{and}\quad bs,sb\in Z. \end{align*} $$
$$ \begin{align*} a<_sb\quad&\Leftrightarrow\quad asb=a,\ as\in N\quad\text{and}\quad bs,sb\in Z,\\ &\Leftrightarrow\quad bsa=a,\ sa\in N\quad\text{and}\quad bs,sb\in Z. \end{align*} $$
Proof. If
![]() $asb=a$
,
$asb=a$
,
![]() $as\in N$
and
$as\in N$
and
![]() $bs,sb\in Z$
then
$bs,sb\in Z$
then
![]() $as\in N$
commutes with
$as\in N$
commutes with
![]() $bs\in Z$
. Thus,
$bs\in Z$
. Thus,
![]() $bsa=bsasb=asbsb=a$
and
$bsa=bsasb=asbsb=a$
and
![]() $bsas=asbs=as\in N$
so
$bsas=asbs=as\in N$
so
![]() $sa=sasb\in N$
, as N is Z-trinormal. Thus,
$sa=sasb\in N$
, as N is Z-trinormal. Thus,
![]() $a<_sb$
, proving the first
$a<_sb$
, proving the first
![]() $\Leftrightarrow $
, while the second follows dually.
$\Leftrightarrow $
, while the second follows dually.
From now on we use the above characterisations of
![]() $<$
.
$<$
.
Proposition 5.5. For all
![]() $a,b',b,c',c\in S$
,
$a,b',b,c',c\in S$
,
Proof. If
![]() $a<_{b'}b<_{c'}c$
then we see that
$a<_{b'}b<_{c'}c$
then we see that
![]() $ac'=ab'bc'\in NN\subseteq N$
and
$ac'=ab'bc'\in NN\subseteq N$
and
![]() $ac'c=ab'bc'c=ab'b=a$
.
$ac'c=ab'bc'c=ab'b=a$
.
We can also switch the subscript with the right argument as follows.
Proposition 5.6. For all
![]() $a,b,c,c'\in S$
,
$a,b,c,c'\in S$
,
Proof. If
![]() $ab\in N$
and
$ab\in N$
and
![]() $b<_{c'}c$
then we see that
$b<_{c'}c$
then we see that
![]() $abc'c\in NZ\subseteq N$
and
$abc'c\in NZ\subseteq N$
and
![]() $abc'cc'=abc'$
.
$abc'cc'=abc'$
.
Next we show that
![]() $<$
preserves the product.
$<$
preserves the product.
Proposition 5.7. For any
![]() $a,b',b,c,d',d\in S$
,
$a,b',b,c,d',d\in S$
,
Proof. If
![]() $a<_{b'}b$
and
$a<_{b'}b$
and
![]() $c<_{d'}d$
then
$c<_{d'}d$
then
![]() $b'bb'acd'=b'acd'\in NN\subseteq N$
so
$b'bb'acd'=b'acd'\in NN\subseteq N$
so
![]() $acd'b'=bb'acd'b'\in N$
, as N is Z-trinormal. Also
$acd'b'=bb'acd'b'\in N$
, as N is Z-trinormal. Also
![]() $acd'b'bd=ab'bcd'd=ac$
, as
$acd'b'bd=ab'bcd'd=ac$
, as
![]() $b'b\in Z$
commutes with
$b'b\in Z$
commutes with
![]() $cd'\in N$
. Moreover, as Z is binormal,
$cd'\in N$
. Moreover, as Z is binormal,
Next we note multiplying by elements of N on the left does not affect
![]() $<$
.
$<$
.
Proposition 5.8. For any
![]() $a,b',b\in S$
and
$a,b',b\in S$
and
![]() $n\in N$
,
$n\in N$
,
Proof. If
![]() $a<_{b'}b$
then
$a<_{b'}b$
then
![]() $nab'\in NN\subseteq N$
and
$nab'\in NN\subseteq N$
and
![]() $nab'b=na$
and hence
$nab'b=na$
and hence
![]() $na<_{b'}b$
, while
$na<_{b'}b$
, while
![]() $an<_{b'}b$
follows by duality.
$an<_{b'}b$
follows by duality.
We also have a similar result for elements of Z.
Proposition 5.9. For any
![]() $a,b,b'\in S$
and
$a,b,b'\in S$
and
![]() $z\in Z$
,
$z\in Z$
,
Proof. If
![]() $az=a<_{b'}b$
then
$az=a<_{b'}b$
then
![]() $b'bz,bzb'\in Z$
and
$b'bz,bzb'\in Z$
and
![]() $ab'bz=az$
, that is,
$ab'bz=az$
, that is,
![]() $a<_{b'}bz$
. Also
$a<_{b'}bz$
. Also
![]() $azb'=ab'\in N$
and
$azb'=ab'\in N$
and
![]() $azb'b=a$
, that is,
$azb'b=a$
, that is,
![]() $a<_{zb'}b$
.
$a<_{zb'}b$
.
We can even split up pairs whose products lie in Z.
Proposition 5.10. For any
![]() $a,b,b',c,c'\in S$
with
$a,b,b',c,c'\in S$
with
![]() $cc',c'c\in Z$
,
$cc',c'c\in Z$
,
Proof. If
![]() $acc'=a<_{b'}b$
and
$acc'=a<_{b'}b$
and
![]() $cc'\in Z$
then
$cc'\in Z$
then
![]() $c'b'bc,bcc'b'\in Z$
,
$c'b'bc,bcc'b'\in Z$
,
![]() $acc'b'bc=ac$
and
$acc'b'bc=ac$
and
![]() $acc'b'=ab'bcc'b'\in NZ\subseteq N$
, that is,
$acc'b'=ab'bcc'b'\in NZ\subseteq N$
, that is,
![]() $ac<_{c'b'}bc$
.
$ac<_{c'b'}bc$
.
For use in the next section, we denote the up-closure of
![]() $A\subseteq S$
by
$A\subseteq S$
by
6 Duals
Definition 6.1. The dual of
![]() $A\subseteq S$
is defined by
$A\subseteq S$
is defined by
So
![]() $s\in A^*$
precisely when some
$s\in A^*$
precisely when some
![]() $a\in A$
is dominated by another element via s. In particular, if
$a\in A$
is dominated by another element via s. In particular, if
![]() $A\subseteq B$
then
$A\subseteq B$
then
![]() $A^*\subseteq B^*$
, a simple fact we often use below. In inverse semigroups, duals are just up-closures of inverses.
$A^*\subseteq B^*$
, a simple fact we often use below. In inverse semigroups, duals are just up-closures of inverses.
Proposition 6.2. If S is an inverse semigroup and
![]() $N=Z=\mathsf {E}(S)$
then
$N=Z=\mathsf {E}(S)$
then
Proof. If
![]() $s\in A^*$
then we have
$s\in A^*$
then we have
![]() $a\in A$
with
$a\in A$
with
![]() $a<_sb$
and hence
$a<_sb$
and hence
![]() $a<_{b^{-1}}b$
, by (5-1), so
$a<_{b^{-1}}b$
, by (5-1), so
Then
![]() $a^{-1}=a^{-1}aa^{-1}=a^{-1}as\in Ns$
so
$a^{-1}=a^{-1}aa^{-1}=a^{-1}as\in Ns$
so
![]() $a^{-1}<s$
, showing that
$a^{-1}<s$
, showing that
![]() $A^*\subseteq A^{-1<}$
.
$A^*\subseteq A^{-1<}$
.
Conversely, if
![]() $s\in A^{-1<\!}$
then we have
$s\in A^{-1<\!}$
then we have
![]() $a\in A$
with
$a\in A$
with
![]() $a^{-1}\!<\!s$
. Again (5-1) yields
$a^{-1}\!<\!s$
. Again (5-1) yields
![]() $a^{-1}\!<_{s^{-1}}s$
. Taking inverses yields
$a^{-1}\!<_{s^{-1}}s$
. Taking inverses yields
![]() $a<_ss^{-1}$
so
$a<_ss^{-1}$
so
![]() $s\in A^*$
, showing that
$s\in A^*$
, showing that
![]() $A^{-1<}\subseteq A^*$
.
$A^{-1<}\subseteq A^*$
.
Again we want to show that duals in structured semigroups still behave much like up-closures of inverses. For example, from (Multiplicativity), we see that the
![]() $^*$
operation is a kind of antimorphism, that is, for all
$^*$
operation is a kind of antimorphism, that is, for all
![]() $A,B\subseteq S$
.
$A,B\subseteq S$
.
Next we note some relations between the
![]() $^*$
and
$^*$
and
![]() $^<$
operations.
$^<$
operations.
Proposition 6.3. For any
![]() $A\subseteq S$
,
$A\subseteq S$
,
Consequently,
![]() $A^*\neq \emptyset $
whenever
$A^*\neq \emptyset $
whenever
![]() $\emptyset \neq A\subseteq A^<$
.
$\emptyset \neq A\subseteq A^<$
.
Proof.
(6-1) If
 $c'\in A^{<*}$
then we have
$c'\in A^{<*}$
then we have
 $a,b,b',c\in S$
with
$a,b,b',c\in S$
with
 $A\ni a<_{b'}b<_{c'}c$
. Then
$A\ni a<_{b'}b<_{c'}c$
. Then
 $a<_{b'bc'}c$
by (Transitivity) and (
Z-Invariance), so
$a<_{b'bc'}c$
by (Transitivity) and (
Z-Invariance), so
 $A^*\ni b'bc'<_cc'\in A^{*<}$
by (Switch).
$A^*\ni b'bc'<_cc'\in A^{*<}$
by (Switch).(6-2) If
 $c\in A^{<<}$
then we have
$c\in A^{<<}$
then we have
 $a,b',b,c'\in S$
with
$a,b',b,c'\in S$
with
 $A\ni a<_{b'}b<_{c'}c$
. Then again
$A\ni a<_{b'}b<_{c'}c$
. Then again
 $A^*\ni b'bc'<_cc'$
and hence
$A^*\ni b'bc'<_cc'$
and hence
 $c\in A^{**}$
.
$c\in A^{**}$
.
For the last statement, note that if
![]() $A^*=\emptyset $
and
$A^*=\emptyset $
and
![]() $A\subseteq A^<$
then (6-2) would yield
$A\subseteq A^<$
then (6-2) would yield
![]() $A\subseteq A^{<<}\subseteq A^{**}\subseteq \emptyset ^*=\emptyset $
.
$A\subseteq A^{<<}\subseteq A^{**}\subseteq \emptyset ^*=\emptyset $
.
If A is closed under ‘triple products’, these inclusions become equalities.
Proposition 6.4. If
![]() $AA^*A\subseteq A$
then
$AA^*A\subseteq A$
then
Proof.
(6-3) Take
 $a'\in A^{*<}$
so we have
$a'\in A^{*<}$
so we have
 $a,b,b',c\in S$
with
$a,b,b',c\in S$
with
 $A\ni c<_{b'}b$
and
$A\ni c<_{b'}b$
and
 $b'<_aa'$
. As
$b'<_aa'$
. As
 $ab'ba'\in Z$
,
$ab'ba'\in Z$
,
 $ba'ab'=bb'\in Z$
and
$ba'ab'=bb'\in Z$
and
 $bb'c=c$
, (
Z-Splitting) and (Switch) yield Then ( N-Invariance) yields
$bb'c=c$
, (
Z-Splitting) and (Switch) yield Then ( N-Invariance) yields $$ \begin{align*} ab'c<_{b'ba'}ab'b<_{a'}a. \end{align*} $$
$$ \begin{align*} ab'c<_{b'ba'}ab'b<_{a'}a. \end{align*} $$
 $cb'ab'c<ab'b<_{a'}a$
and (Transitivity) yields
$cb'ab'c<ab'b<_{a'}a$
and (Transitivity) yields
 $cb'ab'c<_{a'}a$
. Thus
$cb'ab'c<_{a'}a$
. Thus
 $a'\in A^{<*}\cap A^*$
, as showing that
$a'\in A^{<*}\cap A^*$
, as showing that $$ \begin{align*} cb'ab'c\in AA^*A^{**}A^*A\subseteq A(AA^*A)^*A\subseteq AA^*A\subseteq A, \end{align*} $$
$$ \begin{align*} cb'ab'c\in AA^*A^{**}A^*A\subseteq A(AA^*A)^*A\subseteq AA^*A\subseteq A, \end{align*} $$
 $A^{*<}\subseteq A^{<*}\cap A^*$
and hence
$A^{*<}\subseteq A^{<*}\cap A^*$
and hence
 $A^{<*}=A^{*<}\subseteq A^*$
, by (6-1).
$A^{<*}=A^{*<}\subseteq A^*$
, by (6-1).
(6-4) If we take
 $a\in A^{**}$
then we likewise have
$a\in A^{**}$
then we likewise have
 $a',b,b',c\in S$
with
$a',b,b',c\in S$
with
 $A\ni c<_{b'}b$
and
$A\ni c<_{b'}b$
and
 $b'<_aa'$
, which again yields
$b'<_aa'$
, which again yields
 $cb'ab'c<ab'b<a$
and hence
$cb'ab'c<ab'b<a$
and hence
 $a\in A^{<<}$
. Combined with (6-2), this shows that
$a\in A^{<<}$
. Combined with (6-2), this shows that
 $A^{<<}=A^{**}$
.
$A^{<<}=A^{**}$
.
6.1 Diagonality
We can improve some results when N is ‘diagonal’.
Definition 6.5. We call
![]() $D\subseteq S$
diagonal if, for all
$D\subseteq S$
diagonal if, for all
![]() $a,d,b\in S$
,
$a,d,b\in S$
,
Example 6.6. If S is a semigroup of slice-sections of a groupoid bundle
![]() $\pi :F\rightarrow G$
then the canonical diagonal
$\pi :F\rightarrow G$
then the canonical diagonal
![]() $N=\{n\in S:\mathrm {dom}(n)\subseteq G^0\}$
is indeed diagonal in S. To see this just note that if
$N=\{n\in S:\mathrm {dom}(n)\subseteq G^0\}$
is indeed diagonal in S. To see this just note that if
![]() $an,n,nb\in N$
then
$an,n,nb\in N$
then
![]() $anb\in N$
because
$anb\in N$
because
Example 6.7. Any subsemigroup
![]() $I\subseteq S$
of idempotents (for example, all idempotents in an inverse semigroup S) is diagonal, as
$I\subseteq S$
of idempotents (for example, all idempotents in an inverse semigroup S) is diagonal, as
![]() $ai,i,ib\in I$
implies
$ai,i,ib\in I$
implies
![]() $aib=aiib\in II\subseteq I$
.
$aib=aiib\in II\subseteq I$
.
More generally, any regular subsemigroup
![]() $R\subseteq S$
(that is, for every
$R\subseteq S$
(that is, for every
![]() $r\in R$
we have
$r\in R$
we have
![]() $r'\in R$
with
$r'\in R$
with
![]() $rr'r=r$
) is diagonal, as
$rr'r=r$
) is diagonal, as
![]() $ar,r,rb\in R$
yields
$ar,r,rb\in R$
yields
![]() $r'\in R$
with
$r'\in R$
with
Example 6.8. The range of any ‘conditional expectation’
![]() $\Phi $
satisfies (Diagonal): if
$\Phi $
satisfies (Diagonal): if
![]() $R=\mathrm {ran}(\Phi )$
for an idempotent map
$R=\mathrm {ran}(\Phi )$
for an idempotent map
![]() $\Phi $
on S such that, for all
$\Phi $
on S such that, for all
![]() $a,b\in S$
,
$a,b\in S$
,
then
![]() $ar,r,rb\in R$
implies
$ar,r,rb\in R$
implies
![]() $\Phi (arb)=ar\Phi (b)=a\Phi (rb)=arb$
so
$\Phi (arb)=ar\Phi (b)=a\Phi (rb)=arb$
so
![]() $arb\in R$
.
$arb\in R$
.
Diagonality allows us to exchange the subscript and right argument of
![]() $<$
in a slightly more general situation than in (Switch).
$<$
in a slightly more general situation than in (Switch).
Proposition 6.9. If N is diagonal then, for all
![]() $a,b,c,d,d'\in S$
,
$a,b,c,d,d'\in S$
,
Proof. If
![]() $b<_{d'}d$
and
$b<_{d'}d$
and
![]() $ab,bc\in N$
then
$ab,bc\in N$
then
![]() $abcdd'=add'bc=abc$
and (Diagonal) yields
$abcdd'=add'bc=abc$
and (Diagonal) yields
![]() $abcd=add'bcd\in N$
, as
$abcd=add'bcd\in N$
, as
![]() $ab=add'b,d'b,d'bcd\in N$
, that is,
$ab=add'b,d'b,d'bcd\in N$
, that is,
![]() $abc<_dd'$
.
$abc<_dd'$
.
This yields is a kind of transitivity, namely,
Indeed, if
![]() $a<_{b'}b$
and
$a<_{b'}b$
and
![]() $b'<_cc'$
then (Exchange) yields
$b'<_cc'$
then (Exchange) yields
![]() $a=ab'b<_{c'}c$
.
$a=ab'b<_{c'}c$
.
Then (6-3) and (6-4) hold even without the triple product assumption.
Proposition 6.10. If N is diagonal then, for any
![]() $C\subseteq S$
,
$C\subseteq S$
,
Proof. If
![]() $a'\in C^{*<}$
then we have
$a'\in C^{*<}$
then we have
![]() $a,b,b',c\in S$
with
$a,b,b',c\in S$
with
![]() $C\ni c<_{b'}b$
and
$C\ni c<_{b'}b$
and
![]() $b'<_aa'$
. By (*-Transitivity),
$b'<_aa'$
. By (*-Transitivity),
![]() $c<_{a'}a$
and hence
$c<_{a'}a$
and hence
![]() $a'\in C^*$
, showing that
$a'\in C^*$
, showing that
![]() $C^{*<}\subseteq C^*$
.
$C^{*<}\subseteq C^*$
.
If
![]() $a\in C^{**}$
then we have
$a\in C^{**}$
then we have
![]() $a',b,b',c\in S$
with
$a',b,b',c\in S$
with
![]() $C\ni c<_{b'}b$
and
$C\ni c<_{b'}b$
and
![]() $b'<_aa'$
. By (Exchange),
$b'<_aa'$
. By (Exchange),
![]() $c<_{b'}bb'b<_{a'}a$
and hence
$c<_{b'}bb'b<_{a'}a$
and hence
![]() $a\in C^{<<}$
, showing
$a\in C^{<<}$
, showing
![]() $C^{**}\subseteq C^{<<}$
. The reverse inclusion was already proved in (6-2).
$C^{**}\subseteq C^{<<}$
. The reverse inclusion was already proved in (6-2).
Now it follows that
![]() $C^{***}\subseteq C^{*<<}\subseteq C^{*<}\subseteq C^*$
.
$C^{***}\subseteq C^{*<<}\subseteq C^{*<}\subseteq C^*$
.
7 Atlases
Definition 7.1. We call
![]() $A\subseteq S$
an atlas and
$A\subseteq S$
an atlas and
![]() $C\subseteq S$
a coset if
$C\subseteq S$
a coset if
So an atlas is a triple-product-closed round subset, and a coset is also an up-set. These generalise the same notions for inverse semigroups from [Reference Lawson20, Section 1.4 before Proposition 26] (as the order there is reflexive, all subsets are trivially round).
Remark 7.2. When S is a group with identity e and
![]() $N=Z=\{e\}$
, a coset C of S is precisely a coset in the usual sense, specifically a left coset of the subgroup
$N=Z=\{e\}$
, a coset C of S is precisely a coset in the usual sense, specifically a left coset of the subgroup
![]() $C^{-1}C$
or a right coset of the subgroup
$C^{-1}C$
or a right coset of the subgroup
![]() $CC^{-1}$
. In particular, each singleton
$CC^{-1}$
. In particular, each singleton
![]() $\{a\}$
is a coset of the trivial subgroup
$\{a\}$
is a coset of the trivial subgroup
![]() $\{e\}$
.
$\{e\}$
.
More generally, if S is an inverse semigroup and
![]() $N=Z=\mathsf {E}(S)$
then every principal filter
$N=Z=\mathsf {E}(S)$
then every principal filter
![]() $a^{\leq }$
is a coset. If S is the normaliser semigroup of a Cartan subalgebra C of some C*-algebra and
$a^{\leq }$
is a coset. If S is the normaliser semigroup of a Cartan subalgebra C of some C*-algebra and
![]() $N=Z=C$
then again we have principal filters
$N=Z=C$
then again we have principal filters
![]() $a^<$
, for each
$a^<$
, for each
![]() $a\in S$
, which are also cosets, by Proposition 12.3 below. We also have principal filters in the more general structured C*-algebras considered in [Reference Bice2], thanks to [Reference Bice2, Proposition 6.11] and [Reference Bice3, Lemmas 5.2 and 5.3].
$a\in S$
, which are also cosets, by Proposition 12.3 below. We also have principal filters in the more general structured C*-algebras considered in [Reference Bice2], thanks to [Reference Bice2, Proposition 6.11] and [Reference Bice3, Lemmas 5.2 and 5.3].
However, general structured semigroups can have few cosets, for example, S itself is the only nonempty coset in Example 11.4 below. Indeed, an important consequence of one of our results is that we have faithful bundle representations precisely when there are enough cosets to distinguish the elements of S via their corresponding equivalence relations, at least when Z is symmetric; see Corollary 11.3 below.
First we show that atlases generate cosets.
Proposition 7.3. If A is an atlas,
![]() $A^*$
and
$A^*$
and
![]() $A^<=A^{**}(\supseteq A)$
are cosets.
$A^<=A^{**}(\supseteq A)$
are cosets.
Proof. If A is an atlas,
![]() $A^*A^{**}A^*\subseteq (AA^*A)^*\subseteq A^*$
by (Antimorphism). Also
$A^*A^{**}A^*\subseteq (AA^*A)^*\subseteq A^*$
by (Antimorphism). Also
![]() $A^*\subseteq A^{<*}=A^{*<}\subseteq A^*$
by (6-3), that is,
$A^*\subseteq A^{<*}=A^{*<}\subseteq A^*$
by (6-3), that is,
![]() $A^*=A^{*<}$
. This shows that
$A^*=A^{*<}$
. This shows that
![]() $A^*$
is a coset and hence
$A^*$
is a coset and hence
![]() $A^{**}=A^{<<}=A^<$
is also a coset, by (Transitivity),
$A^{**}=A^{<<}=A^<$
is also a coset, by (Transitivity),
![]() $A\subseteq A^<$
and (6-4).
$A\subseteq A^<$
and (6-4).
Proposition 7.4. If
![]() $A,B\subseteq S$
are atlases and
$A,B\subseteq S$
are atlases and
![]() $c\in S$
then
$c\in S$
then
Proof. Assume that
![]() $A,B\subseteq S$
are atlases with
$A,B\subseteq S$
are atlases with
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $A^*=B^*$
. If
$A^*=B^*$
. If
![]() $d\in (Bc)^*$
, then we have
$d\in (Bc)^*$
, then we have
![]() $b\in B$
and
$b\in B$
and
![]() $d'\in S$
with
$d'\in S$
with
![]() $bc<_dd'$
. As
$bc<_dd'$
. As
![]() $A\subseteq A^<$
and
$A\subseteq A^<$
and
![]() $B\subseteq B^<$
, we can take
$B\subseteq B^<$
, we can take
![]() $n\in AA^*\cap N$
,
$n\in AA^*\cap N$
,
![]() $z\in A^*A\cap N$
and
$z\in A^*A\cap N$
and
![]() $b'\in B^*$
with
$b'\in B^*$
with
![]() $b'b\in Z$
. As Z is binormal,
$b'b\in Z$
. As Z is binormal,
![]() $nbzb'\in NZ\subseteq N$
and hence (
N-Invariance) yields
$nbzb'\in NZ\subseteq N$
and hence (
N-Invariance) yields
![]() $nbzb'bc<_dd'$
. Also
$nbzb'bc<_dd'$
. Also
so
![]() $d\in (Ac)^*$
, showing that
$d\in (Ac)^*$
, showing that
![]() $(Bc)^*\subseteq (Ac)^*\subseteq (Bc)^*$
.
$(Bc)^*\subseteq (Ac)^*\subseteq (Bc)^*$
.
Definition 7.5. For any
![]() $A\subseteq S$
and
$A\subseteq S$
and
![]() $b\in S$
we define
$b\in S$
we define
 $$ \begin{align*} A|b\quad&\Leftrightarrow\quad\text{there exists } b'\in S\ (bb',b'b\in Z\quad\text{and}\quad\text{there exists } a\in A\ (a=abb')),\\ b|A\quad&\Leftrightarrow\quad\text{there exists } b'\in S\ (bb',b'b\in Z\quad\text{and}\quad\text{there exists } a\in A\ (a=b'ba)). \end{align*} $$
$$ \begin{align*} A|b\quad&\Leftrightarrow\quad\text{there exists } b'\in S\ (bb',b'b\in Z\quad\text{and}\quad\text{there exists } a\in A\ (a=abb')),\\ b|A\quad&\Leftrightarrow\quad\text{there exists } b'\in S\ (bb',b'b\in Z\quad\text{and}\quad\text{there exists } a\in A\ (a=b'ba)). \end{align*} $$
We read
![]() $A|b$
and
$A|b$
and
![]() $b|A$
as saying b acts on A (from the right and left, respectively). Indeed, when b acts on A, the product is another atlas; see Proposition 7.7 below.
$b|A$
as saying b acts on A (from the right and left, respectively). Indeed, when b acts on A, the product is another atlas; see Proposition 7.7 below.
Proposition 7.6. If
![]() $A,B\subseteq S$
are atlases satisfying
$A,B\subseteq S$
are atlases satisfying
![]() $A^*A\subseteq (BB^*)^<$
then their product
$A^*A\subseteq (BB^*)^<$
then their product
![]() $AB$
is also an atlas. Consequently,
$AB$
is also an atlas. Consequently,
![]() $(AB)^*$
is a coset and, for all
$(AB)^*$
is a coset and, for all
![]() $a\in A$
,
$a\in A$
,
Proof. If
![]() $A^*A\subseteq (BB^*)^<$
then (Multiplicativity) and the fact B is an atlas yields
$A^*A\subseteq (BB^*)^<$
then (Multiplicativity) and the fact B is an atlas yields
![]() $A^*AB\subseteq (BB^*)^<B^<\subseteq (BB^*B)^<\subseteq B^<$
and hence
$A^*AB\subseteq (BB^*)^<B^<\subseteq (BB^*B)^<\subseteq B^<$
and hence
Thus,
![]() $AB(AB)^*AB\subseteq ABB^*B\subseteq AB\subseteq A^<B^<\subseteq (AB)^<$
by (Multiplicativity), so
$AB(AB)^*AB\subseteq ABB^*B\subseteq AB\subseteq A^<B^<\subseteq (AB)^<$
by (Multiplicativity), so
![]() $AB$
is an atlas.
$AB$
is an atlas.
Take
![]() $a',c\in S$
with
$a',c\in S$
with
![]() $A\ni c<_{a'}a$
. Then
$A\ni c<_{a'}a$
. Then
![]() $a'c\in A^*A\subseteq (BB^*)^<$
so, taking any
$a'c\in A^*A\subseteq (BB^*)^<$
so, taking any
![]() $b\in B$
,
$b\in B$
,
![]() $a'cb\in (BB^*)^<B\subseteq B^<$
. Taking
$a'cb\in (BB^*)^<B\subseteq B^<$
. Taking
![]() $e,d\in S$
with
$e,d\in S$
with
![]() $B\ni e<_da'cb$
, we see that
$B\ni e<_da'cb$
, we see that
![]() $a'ae=a'aa'cbde=a'cbde=e$
so
$a'ae=a'aa'cbde=a'cbde=e$
so
![]() $a|B$
. For any other
$a|B$
. For any other
![]() $f\in A$
, (
N-Invariance) yields
$f\in A$
, (
N-Invariance) yields
by (7-1) (applied to
![]() $S^{\mathrm {op}}$
with a,
$S^{\mathrm {op}}$
with a,
![]() $B^<$
and B in place of c, A and B, respectively). This shows that
$B^<$
and B in place of c, A and B, respectively). This shows that
![]() $(AB)^*\subseteq (aB)^*\subseteq (AB)^*$
.
$(AB)^*\subseteq (aB)^*\subseteq (AB)^*$
.
Note that we can take
![]() $B=A^*$
above, as
$B=A^*$
above, as
![]() $A^*A\subseteq A^{<*}A^<\subseteq (A^*A)^<$
, that is,
$A^*A\subseteq A^{<*}A^<\subseteq (A^*A)^<$
, that is,
In this case, the cosets
![]() $(AA^*)^*$
and
$(AA^*)^*$
and
![]() $(AA^*)^<$
they generate are the same as
$(AA^*)^<$
they generate are the same as
![]() $(AA^*)^*\subseteq (A^{**}A^*)^*\subseteq (AA^*)^{**}=(AA^*)^<$
and
$(AA^*)^*\subseteq (A^{**}A^*)^*\subseteq (AA^*)^{**}=(AA^*)^<$
and
![]() $(AA^*)^<\subseteq (A^{**}A^*)^<\subseteq (AA^*)^{*<}=(AA^*)^*$
. Likewise,
$(AA^*)^<\subseteq (A^{**}A^*)^<\subseteq (AA^*)^{*<}=(AA^*)^*$
. Likewise,
![]() $(A^*A)^*$
and
$(A^*A)^*$
and
![]() $(A^*A)^<$
coincide, and we denote these cosets by
$(A^*A)^<$
coincide, and we denote these cosets by
We soon see that these are the source and range in a groupoid of cosets.
Proposition 7.7. If
![]() $A|b$
and A is an atlas then
$A|b$
and A is an atlas then
![]() $Ab$
is an atlas with
$Ab$
is an atlas with
Proof. Take
![]() $b'\in S$
with
$b'\in S$
with
![]() $bb',b'b\in Z$
and
$bb',b'b\in Z$
and
![]() $a\in A$
with
$a\in A$
with
![]() $a=abb'$
. As
$a=abb'$
. As
![]() $A\subseteq A^<$
, we can also take
$A\subseteq A^<$
, we can also take
![]() $a'\in A^*$
with
$a'\in A^*$
with
![]() $aa',a'a\in Z$
.
$aa',a'a\in Z$
.
First, note that
To see this, take any
![]() $c'\in A^*$
, so we have
$c'\in A^*$
, so we have
![]() $c,d\in S$
with
$c,d\in S$
with
![]() $A\ni d<_{c'}c$
. Then (
N-Invariance) yields
$A\ni d<_{c'}c$
. Then (
N-Invariance) yields
![]() $da'a<_{c'}c$
and (
Z-Splitting) yields
$da'a<_{c'}c$
and (
Z-Splitting) yields
![]() $da'ab<_{b'c'}cb$
. Thus
$da'ab<_{b'c'}cb$
. Thus
![]() $b'c'\in (Ab)^*$
, as
$b'c'\in (Ab)^*$
, as
![]() $da'a\in AA^*A\subseteq A$
, showing that
$da'a\in AA^*A\subseteq A$
, showing that
![]() $b'A^*\subseteq (Ab)^*$
.
$b'A^*\subseteq (Ab)^*$
.
Next we claim that
To see this, take
![]() $c'\in (Ab)^*$
, so we have
$c'\in (Ab)^*$
, so we have
![]() $c\in S$
and
$c\in S$
and
![]() $d\in A$
with
$d\in A$
with
![]() $db<_{c'}c$
. Take
$db<_{c'}c$
. Take
![]() $d'\in A^*$
with
$d'\in A^*$
with
![]() $dd',d'd\in Z$
and let
$dd',d'd\in Z$
and let
![]() $n=da'ad'\in N$
so (
N-Invariance) yields
$n=da'ad'\in N$
so (
N-Invariance) yields
![]() $ndb<_{c'}c$
. Also
$ndb<_{c'}c$
. Also
![]() $ndbb'=da'ad'dbb'=da'abb'd'd=da'ad'd=nd$
and hence
$ndbb'=da'ad'dbb'=da'abb'd'd=da'ad'd=nd$
and hence
![]() $ndbb'b=ndb$
so (
Z-Splitting) yields
$ndbb'b=ndb$
so (
Z-Splitting) yields
![]() $nd=ndbb'<_{bc'}cb'$
. Thus
$nd=ndbb'<_{bc'}cb'$
. Thus
![]() $bc'\in A^*$
, as
$bc'\in A^*$
, as
![]() $nd\in AA^*AA^*A\subseteq A$
, showing that
$nd\in AA^*AA^*A\subseteq A$
, showing that
![]() $b(Ab)^*\subseteq A^*$
and hence
$b(Ab)^*\subseteq A^*$
and hence
Next, note that
![]() $a'aa'=a'abb'a'=bb'a'aa'$
, so b and
$a'aa'=a'abb'a'=bb'a'aa'$
, so b and
![]() $a'aa'\in A^*AA^*\subseteq A^*$
witness
$a'aa'\in A^*AA^*\subseteq A^*$
witness
![]() $b'|A^*$
. Thus, (7-3) applied in
$b'|A^*$
. Thus, (7-3) applied in
![]() $S^{\mathrm {op}}$
yields
$S^{\mathrm {op}}$
yields
![]() $A^{**}b\subseteq (b'A^*)^*$
. Then (6-4) and (7-4) yield
$A^{**}b\subseteq (b'A^*)^*$
. Then (6-4) and (7-4) yield
showing that
![]() $Ab$
is an atlas.
$Ab$
is an atlas.
Note that
![]() $Ab(Ab)^*\subseteq AA^*\subseteq A^{**}(Abb')^*\subseteq (Abb'A^*)^*\subseteq (Ab(Ab)^*)^*=\mathsf {r}(Ab)$
, so taking duals yields
$Ab(Ab)^*\subseteq AA^*\subseteq A^{**}(Abb')^*\subseteq (Abb'A^*)^*\subseteq (Ab(Ab)^*)^*=\mathsf {r}(Ab)$
, so taking duals yields
![]() $\mathsf {r}(Ab)\subseteq \mathsf {r}(A)\subseteq \mathsf {r}(Ab)^*=\mathsf {r}(Ab)$
.
$\mathsf {r}(Ab)\subseteq \mathsf {r}(A)\subseteq \mathsf {r}(Ab)^*=\mathsf {r}(Ab)$
.
Proposition 7.8. If
![]() $A\subseteq S$
is an atlas and
$A\subseteq S$
is an atlas and
![]() $n\in N$
then
$n\in N$
then
Proof. If
![]() $n\in \mathsf {s}(A)$
then
$n\in \mathsf {s}(A)$
then
![]() $An\subseteq A^<(A^*A)^<\subseteq (AA^*A)^<\subseteq A^<$
and hence
$An\subseteq A^<(A^*A)^<\subseteq (AA^*A)^<\subseteq A^<$
and hence
Also, we have
![]() $m,n'\in S$
with
$m,n'\in S$
with
![]() $A^*A\ni m<_nn'$
, so
$A^*A\ni m<_nn'$
, so
![]() $nn',n'n\in Z$
and
$nn',n'n\in Z$
and
![]() $mnn'=m$
. Taking any
$mnn'=m$
. Taking any
![]() $a\in A$
, note that
$a\in A$
, note that
![]() $am\in AA^*A\subseteq A$
and
$am\in AA^*A\subseteq A$
and
![]() $amnn'=am$
, showing
$amnn'=am$
, showing
![]() $A|n$
.
$A|n$
.
Conversely, if
![]() $A|n$
, we have
$A|n$
, we have
![]() $n'\in S$
with
$n'\in S$
with
![]() $nn',n'n\in Z$
and
$nn',n'n\in Z$
and
![]() $a\in A$
with
$a\in A$
with
![]() $a=ann'$
. Then
$a=ann'$
. Then
![]() $a'a=a'ann'$
, for any
$a'a=a'ann'$
, for any
![]() $a'\in A^*$
with
$a'\in A^*$
with
![]() $a'a\in N$
, so
$a'a\in N$
, so
![]() $a'a<_nn'$
and
$a'a<_nn'$
and
![]() $n\in \mathsf {s}(A)$
.
$n\in \mathsf {s}(A)$
.
8 Cosets
Our goal here is to show that the nonempty cosets
form an étale groupoid. This generalises similar results for filters in inverse semigroups in [Reference Lawson, Margolis and Steinberg23, Reference Lenz24] (we have more to say about filters in Section 12).
Theorem 8.1.
![]() $\mathcal {C}(S)$
is a groupoid with inverse
$\mathcal {C}(S)$
is a groupoid with inverse
![]() $C\mapsto C^*$
and product
$C\mapsto C^*$
and product
Proof. If
![]() $(B,C)\in \mathcal {C}^2=\{(B,C):B,C\in \mathcal {C}(S)\ \text {and}\ \mathsf {s}(B)=\mathsf {r}(C)\}$
then
$(B,C)\in \mathcal {C}^2=\{(B,C):B,C\in \mathcal {C}(S)\ \text {and}\ \mathsf {s}(B)=\mathsf {r}(C)\}$
then
![]() $(BC)^<$
is a coset, by Propositions 7.3 and 7.6. Also, as
$(BC)^<$
is a coset, by Propositions 7.3 and 7.6. Also, as
![]() $B\neq \emptyset \neq C$
, it follows that
$B\neq \emptyset \neq C$
, it follows that
![]() $\emptyset \neq BC\subseteq B^<C^<\subseteq (BC)^<$
, so the product is well defined on
$\emptyset \neq BC\subseteq B^<C^<\subseteq (BC)^<$
, so the product is well defined on
![]() $\mathcal {C}(S)$
. Moreover, if
$\mathcal {C}(S)$
. Moreover, if
![]() $c\in C$
, Proposition 7.6 yields
$c\in C$
, Proposition 7.6 yields
![]() $B|c$
and
$B|c$
and
![]() $(BC)^<=(Bc)^<$
, so Proposition 7.7 yields
$(BC)^<=(Bc)^<$
, so Proposition 7.7 yields
Thus,
![]() $(A,B)\in \mathcal {C}^2$
if and only if
$(A,B)\in \mathcal {C}^2$
if and only if
![]() $(A,(BC)^<)\in \mathcal {C}^2$
, in which case, for any
$(A,(BC)^<)\in \mathcal {C}^2$
, in which case, for any
![]() $c\in C$
,
$c\in C$
,
Likewise, for any
![]() $(A,B)\in \mathcal {C}^2$
, we see that
$(A,B)\in \mathcal {C}^2$
, we see that
![]() $\mathsf {s}((AB)^<)=\mathsf {s}(B)$
, so
$\mathsf {s}((AB)^<)=\mathsf {s}(B)$
, so
![]() $((AB)^<,C)\in \mathcal {C}^2$
if and only if
$((AB)^<,C)\in \mathcal {C}^2$
if and only if
![]() $(B,C)\in \mathcal {C}^2$
, in which case
$(B,C)\in \mathcal {C}^2$
, in which case
![]() $((AB)^<C)^<=(ABC)^<=(A(BC)^<)^<$
, showing that the product is associative.
$((AB)^<C)^<=(ABC)^<=(A(BC)^<)^<$
, showing that the product is associative.
Again by Proposition 7.3, as well as the last part of Proposition 6.3, if
![]() $C\in \mathcal {C}(S)$
then
$C\in \mathcal {C}(S)$
then
![]() $C^*\in \mathcal {C}(S)$
, so the involution is well defined on
$C^*\in \mathcal {C}(S)$
, so the involution is well defined on
![]() $\mathcal {C}(S)$
. Also, for any
$\mathcal {C}(S)$
. Also, for any
![]() $(B,C)\in \mathcal {C}^2$
,
$(B,C)\in \mathcal {C}^2$
,
![]() $c\in C$
and
$c\in C$
and
![]() $c'\in C^*$
with
$c'\in C^*$
with
![]() $cc'\in N$
,
$cc'\in N$
,
showing that
![]() $C\cdot C^*$
is a unit. Likewise,
$C\cdot C^*$
is a unit. Likewise,
![]() $(B^*BC)^<=C$
so
$(B^*BC)^<=C$
so
![]() $B^*\cdot B$
is a unit, showing that the involution takes each element to its inverse. Thus,
$B^*\cdot B$
is a unit, showing that the involution takes each element to its inverse. Thus,
![]() $\mathcal {C}(S)$
is a groupoid.
$\mathcal {C}(S)$
is a groupoid.
The units of this groupoid have a couple of simple characterisations.
Proposition 8.2.
![]() $C\in \mathcal {C}(S)$
is a unit if and only if
$C\in \mathcal {C}(S)$
is a unit if and only if
![]() $C\cap N\neq \emptyset $
if and only if
$C\cap N\neq \emptyset $
if and only if
![]() $C\cap Z\neq \emptyset $
.
$C\cap Z\neq \emptyset $
.
Proof. If
![]() $C\in \mathcal {C}(S)$
is a unit then
$C\in \mathcal {C}(S)$
is a unit then
![]() $C=(CC^*)^<\supseteq CC^*$
. Taking any
$C=(CC^*)^<\supseteq CC^*$
. Taking any
![]() $b,b',c\in S$
with
$b,b',c\in S$
with
![]() $C\ni c<_{b'}b$
, we see that
$C\ni c<_{b'}b$
, we see that
![]() $bb'\in CC^*\cap Z\subseteq C\cap Z$
. Conversely, if
$bb'\in CC^*\cap Z\subseteq C\cap Z$
. Conversely, if
![]() $n\in C\cap N$
then, for any B with
$n\in C\cap N$
then, for any B with
![]() $(B,C)\in \mathcal {C}^2$
, Proposition 7.6 and (7-5) yield
$(B,C)\in \mathcal {C}^2$
, Proposition 7.6 and (7-5) yield
![]() $B=(Bn)^<=(BC)^<$
. Likewise,
$B=(Bn)^<=(BC)^<$
. Likewise,
![]() $B=(CB)^<$
for any B with
$B=(CB)^<$
for any B with
![]() $(C,B)\in \mathcal {C}^2$
, so C is a unit in
$(C,B)\in \mathcal {C}^2$
, so C is a unit in
![]() $\mathcal {C}(S)$
.
$\mathcal {C}(S)$
.
The following slices of
![]() $\mathcal {C}(S)$
will play an important role very soon.
$\mathcal {C}(S)$
will play an important role very soon.
Proposition 8.3. For every
![]() $a\in S$
, we have a slice in
$a\in S$
, we have a slice in
![]() $\mathcal {C}(S)$
given by
$\mathcal {C}(S)$
given by
Proof. If
![]() $B,C\in \mathcal {C}_a$
and
$B,C\in \mathcal {C}_a$
and
![]() $\mathsf {s}(B)=\mathsf {s}(C)$
then, by (7-2),
$\mathsf {s}(B)=\mathsf {s}(C)$
then, by (7-2),
Likewise,
![]() $\mathsf {r}(B)=\mathsf {r}(C)$
implies
$\mathsf {r}(B)=\mathsf {r}(C)$
implies
![]() $B=C$
, so
$B=C$
, so
![]() $\mathcal {C}_a$
is a slice.
$\mathcal {C}_a$
is a slice.
The canonical topology on
![]() $\mathcal {C}(S)$
is generated by the slices
$\mathcal {C}(S)$
is generated by the slices
![]() $(\mathcal {C}_a)_{a\in S}$
. So a basis for this topology is given by
$(\mathcal {C}_a)_{a\in S}$
. So a basis for this topology is given by
![]() $\mathcal {C}_F=\bigcap _{f\in F}\mathcal {C}_f$
, for finite
$\mathcal {C}_F=\bigcap _{f\in F}\mathcal {C}_f$
, for finite
![]() $F\subseteq S$
.
$F\subseteq S$
.
Theorem 8.4. The coset groupoid is étale in the canonical topology.
Proof. If
![]() $C^*\in \mathcal {C}_b$
then
$C^*\in \mathcal {C}_b$
then
![]() $b\in C^*$
, so we have
$b\in C^*$
, so we have
![]() $a,b'\in S$
with
$a,b'\in S$
with
![]() $C\ni a<_bb'$
and hence
$C\ni a<_bb'$
and hence
![]() $C\in \mathcal {C}_a$
and
$C\in \mathcal {C}_a$
and
![]() $\mathcal {C}_a^*\subseteq \mathcal {C}_b$
, showing that the involution
$\mathcal {C}_a^*\subseteq \mathcal {C}_b$
, showing that the involution
![]() $C\mapsto C^*$
is continuous on
$C\mapsto C^*$
is continuous on
![]() $\mathcal {C}(S)$
. Similarly, if
$\mathcal {C}(S)$
. Similarly, if
![]() $B\cdot C\in \mathcal {C}_a$
then
$B\cdot C\in \mathcal {C}_a$
then
![]() $a\in B\cdot C$
, so we have
$a\in B\cdot C$
, so we have
![]() $b\in B$
and
$b\in B$
and
![]() $c\in C$
with
$c\in C$
with
![]() $bc<a$
, that is,
$bc<a$
, that is,
![]() $B\in \mathcal {C}_b$
,
$B\in \mathcal {C}_b$
,
![]() $C\in \mathcal {C}_c$
and
$C\in \mathcal {C}_c$
and
![]() $\mathcal {C}_b\cdot \mathcal {C}_c\subseteq \mathcal {C}_a$
, showing that the product is also continuous.
$\mathcal {C}_b\cdot \mathcal {C}_c\subseteq \mathcal {C}_a$
, showing that the product is also continuous.
To see that the source
![]() $\mathsf {s}$
is an open map on
$\mathsf {s}$
is an open map on
![]() $\mathcal {C}(S)$
, take any finite
$\mathcal {C}(S)$
, take any finite
![]() $F\subseteq S$
and
$F\subseteq S$
and
![]() $C\in \mathcal {C}_F$
. Further, take finite
$C\in \mathcal {C}_F$
. Further, take finite
![]() $G\subseteq C$
with
$G\subseteq C$
with
![]() $F\subseteq G^<$
and fix some
$F\subseteq G^<$
and fix some
![]() $a,b',b\in S$
with
$a,b',b\in S$
with
![]() $G\ni a<_{b'}b\in F$
. We claim that
$G\ni a<_{b'}b\in F$
. We claim that
To see this, first note that
![]() $b'\in G^*\subseteq C^*$
and
$b'\in G^*\subseteq C^*$
and
![]() $G\subseteq C$
imply
$G\subseteq C$
imply
![]() $b'G\subseteq C^*C\subseteq \mathsf {s}(C)$
and hence
$b'G\subseteq C^*C\subseteq \mathsf {s}(C)$
and hence
![]() $\mathsf {s}(C)\in \mathcal {C}_{b'G}$
. Next note that if
$\mathsf {s}(C)\in \mathcal {C}_{b'G}$
. Next note that if
![]() $B\in \mathcal {C}_{b'G}$
then
$B\in \mathcal {C}_{b'G}$
then
![]() $b'a\in B\cap N$
so B is a unit, by Proposition 8.2, and
$b'a\in B\cap N$
so B is a unit, by Proposition 8.2, and
![]() $b'bb'a=b'a$
so
$b'bb'a=b'a$
so
![]() $b|B$
and
$b|B$
and
![]() $(bB)^<\in \mathcal {C}_{bb'G}\subseteq \mathcal {C}_F$
(as
$(bB)^<\in \mathcal {C}_{bb'G}\subseteq \mathcal {C}_F$
(as
![]() $A\in \mathcal {C}_{bb'G}$
implies
$A\in \mathcal {C}_{bb'G}$
implies
![]() $bb'G\subseteq A$
and hence
$bb'G\subseteq A$
and hence
![]() $F\subseteq G^<\subseteq (bb'G)^<\subseteq A^<\subseteq A$
). Thus
$F\subseteq G^<\subseteq (bb'G)^<\subseteq A^<\subseteq A$
). Thus
![]() $B=\mathsf {s}(B)=\mathsf {s}(bB)\in \mathsf {s}[\mathcal {C}_F]$
, showing that
$B=\mathsf {s}(B)=\mathsf {s}(bB)\in \mathsf {s}[\mathcal {C}_F]$
, showing that
![]() $\mathcal {C}_{b'G}\subseteq \mathsf {s}[\mathcal {C}_F]$
. As C was arbitrary, this shows
$\mathcal {C}_{b'G}\subseteq \mathsf {s}[\mathcal {C}_F]$
. As C was arbitrary, this shows
![]() $\mathsf {s}[\mathcal {C}_F]$
is open, which, as F was arbitrary, shows that
$\mathsf {s}[\mathcal {C}_F]$
is open, which, as F was arbitrary, shows that
![]() $\mathsf {s}$
is an open map.
$\mathsf {s}$
is an open map.
8.1 Symmetry
The structured semigroups we are interested in often satisfy a certain additional assumption, which also allows us to say more about cosets.
Definition 8.5. We call
![]() $Y\subseteq S$
symmetric if, for all
$Y\subseteq S$
symmetric if, for all
![]() $a,b\in S$
,
$a,b\in S$
,
For example, the idempotents
![]() $\mathsf {E}(S)$
in any semigroup S are always symmetric, as
$\mathsf {E}(S)$
in any semigroup S are always symmetric, as
![]() $ab\in \mathsf {E}(S)$
implies
$ab\in \mathsf {E}(S)$
implies
![]() $b(ababab)a=baba\in \mathsf {E}(S)$
. Likewise, one can verify that the slice-sections
$b(ababab)a=baba\in \mathsf {E}(S)$
. Likewise, one can verify that the slice-sections
![]() $\mathcal {S}(\pi |_{F^{\times }})$
of the invertible part of a Fell bundle
$\mathcal {S}(\pi |_{F^{\times }})$
of the invertible part of a Fell bundle
![]() $\pi $
have a symmetric central-diagonal
$\pi $
have a symmetric central-diagonal
![]() $\mathcal {Z}(\pi |_{F^{\times }})$
(see Example 3.9).
$\mathcal {Z}(\pi |_{F^{\times }})$
(see Example 3.9).
Symmetry yields more one-sided versions of
![]() $<$
than in Proposition 5.4.
$<$
than in Proposition 5.4.
Proposition 8.6. If Z is symmetric and
![]() $a,b\in S$
then
$a,b\in S$
then
 $$ \begin{align*} asb=a,\ as\in N\quad\text{and}\quad(bs\in Z\quad\text{or }sb\in Z)\ &\Rightarrow\ a<_sbsb\quad\text{and}\quad a<_{sbs}b.\\ bsa=a,\ sa\in N\quad\text{and}\quad(bs\in Z\quad\text{or }sb\in Z)\ &\Rightarrow\ a<_sbsb\quad\text{and}\quad a<_{sbs}b. \end{align*} $$
$$ \begin{align*} asb=a,\ as\in N\quad\text{and}\quad(bs\in Z\quad\text{or }sb\in Z)\ &\Rightarrow\ a<_sbsb\quad\text{and}\quad a<_{sbs}b.\\ bsa=a,\ sa\in N\quad\text{and}\quad(bs\in Z\quad\text{or }sb\in Z)\ &\Rightarrow\ a<_sbsb\quad\text{and}\quad a<_{sbs}b. \end{align*} $$
Proof. If
![]() $bs\in Z$
then
$bs\in Z$
then
![]() $bsbs\in ZZ\subseteq Z$
and
$bsbs\in ZZ\subseteq Z$
and
![]() $sbsb\in Z$
, by symmetry. If
$sbsb\in Z$
, by symmetry. If
![]() $sb\in Z$
then, likewise,
$sb\in Z$
then, likewise,
![]() $sbsb\in ZZ\subseteq Z$
and
$sbsb\in ZZ\subseteq Z$
and
![]() $bsbs\in Z$
, by symmetry. If
$bsbs\in Z$
, by symmetry. If
![]() $asb=a$
and
$asb=a$
and
![]() $as\in N$
too then
$as\in N$
too then
![]() $asbs\in NZ\subseteq N$
and
$asbs\in NZ\subseteq N$
and
![]() $asbsb=asb=a$
, so
$asbsb=asb=a$
, so
![]() $a<_sbsb$
and
$a<_sbsb$
and
![]() $a<_{sbs}b$
. This proves the first
$a<_{sbs}b$
. This proves the first
![]() $\Rightarrow $
and the second follows by a dual argument.
$\Rightarrow $
and the second follows by a dual argument.
Proposition 8.7. If Z is symmetric then, for all
![]() $a,b\in S$
and
$a,b\in S$
and
![]() $n\in N$
,
$n\in N$
,
If N is diagonal and Z is symmetric then, for all
![]() $a,b\in S$
and
$a,b\in S$
and
![]() $n\in N$
,
$n\in N$
,
Proof. If
![]() $a<_{b'}nb$
then
$a<_{b'}nb$
then
![]() $ab'n\in NN\subseteq N$
,
$ab'n\in NN\subseteq N$
,
![]() $ab'nb=a$
and
$ab'nb=a$
and
![]() $b'nb\in Z$
so
$b'nb\in Z$
so
![]() $a<_{b'nbb'n}b$
, by Proposition 8.6 with
$a<_{b'nbb'n}b$
, by Proposition 8.6 with
![]() $s=b'n$
.
$s=b'n$
.
Now suppose that N is also diagonal and
![]() $a<_{b'n}b$
. In particular,
$a<_{b'n}b$
. In particular,
![]() $bb'n\in Z$
so, by symmetry,
$bb'n\in Z$
so, by symmetry,
![]() ${nbb'nbb'\in Z\subseteq N}$
. As
${nbb'nbb'\in Z\subseteq N}$
. As
![]() $ab'n,n\in N$
too, diagonality yields
$ab'n,n\in N$
too, diagonality yields
![]() ${ab'=ab'nbb'nbb'\in N}$
. As
${ab'=ab'nbb'nbb'\in N}$
. As
![]() $ab'nb=a$
and
$ab'nb=a$
and
![]() $b'nb\in Z$
, it follows that
$b'nb\in Z$
, it follows that
![]() $a<_{b'}nbb'nb$
, again by Proposition 8.6 but with
$a<_{b'}nbb'nb$
, again by Proposition 8.6 but with
![]() $s=b'$
and
$s=b'$
and
![]() $nb$
replacing b.
$nb$
replacing b.
Proposition 8.8. If Z is symmetric,
![]() $A\subseteq S$
is an atlas and
$A\subseteq S$
is an atlas and
![]() $a,b',b\in S$
, then
$a,b',b\in S$
, then
Proof. If
![]() $bb'\in Z$
then
$bb'\in Z$
then
![]() $b'bb'b\in Z$
by symmetry. Also
$b'bb'b\in Z$
by symmetry. Also
![]() $bb'bb'\in ZZ\subseteq Z$
and
$bb'bb'\in ZZ\subseteq Z$
and
![]() $abb'bb'=abb'=a$
, showing that
$abb'bb'=abb'=a$
, showing that
![]() $b'bb'$
witnesses
$b'bb'$
witnesses
![]() $A|b$
.
$A|b$
.
Let us now extend our notion of étale representation from Section 2.2.
Definition 8.9. An étale representation of the structured semigroup
![]() $(S,N,Z)$
on an étale groupoid G is a semigroup homomorphism
$(S,N,Z)$
on an étale groupoid G is a semigroup homomorphism
![]() $\theta :S\rightarrow \mathcal {B}(G)$
to the open slices of G such that
$\theta :S\rightarrow \mathcal {B}(G)$
to the open slices of G such that
![]() $\theta [S]$
covers G,
$\theta [S]$
covers G,
![]() $\theta [N]\subseteq \mathcal {O}(G^0)$
and, for all
$\theta [N]\subseteq \mathcal {O}(G^0)$
and, for all
![]() $g\in G$
and
$g\in G$
and
![]() $a\in S$
,
$a\in S$
,
Intuitively, (Locally Round) is saying we can always shrink open neighbourhoods arising from the representation. On a more technical level, we must restrict the representations in this way for the coset representation to be universal, as shown below. The following observation shows that we can at least rest assured that requiring (Locally Round) and
![]() $\theta [N]\subseteq \mathcal {O}(G^0)$
is still consistent with the original notion of an étale representation of an inverse semigroup introduced in Section 2.2.
$\theta [N]\subseteq \mathcal {O}(G^0)$
is still consistent with the original notion of an étale representation of an inverse semigroup introduced in Section 2.2.
Proposition 8.10. If S is an inverse semigroup and
![]() $N=Z=\mathsf {E}(S)$
then any semigroup homomorphism
$N=Z=\mathsf {E}(S)$
then any semigroup homomorphism
![]() $\theta :S\rightarrow \mathcal {B}(G)$
is an étale representation.
$\theta :S\rightarrow \mathcal {B}(G)$
is an étale representation.
Proof. As
![]() $\theta $
is semigroup homomorphism, it maps idempotents in S to idempotents in
$\theta $
is semigroup homomorphism, it maps idempotents in S to idempotents in
![]() $\mathcal {B}(G)$
, which are precisely the open subsets of the unit space
$\mathcal {B}(G)$
, which are precisely the open subsets of the unit space
![]() $G^0$
, that is,
$G^0$
, that is,
![]() $\theta [\mathsf {E}(S)]\subseteq \mathcal {O}(G^0)$
. Moreover, the domination relation
$\theta [\mathsf {E}(S)]\subseteq \mathcal {O}(G^0)$
. Moreover, the domination relation
![]() $<$
here is just the usual order on the inverse semigroup S; see (5-1). In particular,
$<$
here is just the usual order on the inverse semigroup S; see (5-1). In particular,
![]() $<$
is reflexive so (Locally Round) is immediately verified by taking
$<$
is reflexive so (Locally Round) is immediately verified by taking
![]() $b=a$
.
$b=a$
.
As before in Section 2.2, we call an étale representation
![]() $\mu :S\rightarrow \mathcal {B}(G)$
universal if, for every étale representation
$\mu :S\rightarrow \mathcal {B}(G)$
universal if, for every étale representation
![]() $\theta :S\rightarrow \mathcal {B}(H)$
, there exists a unique étale morphism
$\theta :S\rightarrow \mathcal {B}(H)$
, there exists a unique étale morphism
![]() $\phi :H\rightarrow G$
such that
$\phi :H\rightarrow G$
such that
![]() $\theta =\overline \phi \circ \mu $
, where
$\theta =\overline \phi \circ \mu $
, where
![]() $\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
is the preimage map. Again as before, we let
$\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
is the preimage map. Again as before, we let
![]() $\mathcal {C}$
denote the map
$\mathcal {C}$
denote the map
![]() $a\mapsto \mathcal {C}_a$
.
$a\mapsto \mathcal {C}_a$
.
Theorem 8.11. If Z is symmetric,
![]() $\mathcal {C}$
is a universal étale representation.
$\mathcal {C}$
is a universal étale representation.
Proof. First, we must show that
![]() $\mathcal {C}$
is a semigroup homomorphism. For
$\mathcal {C}$
is a semigroup homomorphism. For
![]() $a,b\in S$
, certainly
$a,b\in S$
, certainly
![]() $\mathcal {C}_a\cdot \mathcal {C}_b\subseteq \mathcal {C}_{ab}$
. Next, for
$\mathcal {C}_a\cdot \mathcal {C}_b\subseteq \mathcal {C}_{ab}$
. Next, for
![]() $n\in N$
, we have a partial converse, namely,
$n\in N$
, we have a partial converse, namely,
Indeed, if
![]() $C\in \mathcal {C}_{an}$
then we have
$C\in \mathcal {C}_{an}$
then we have
![]() $c\in C$
with
$c\in C$
with
![]() $c<an$
. This implies
$c<an$
. This implies
![]() $c<a$
, by (8-1), and hence
$c<a$
, by (8-1), and hence
![]() $a\in C^<\subseteq C$
, that is,
$a\in C^<\subseteq C$
, that is,
![]() $C\in \mathcal {C}_a$
, which proves (8-3).
$C\in \mathcal {C}_a$
, which proves (8-3).
More generally, if
![]() $C\in \mathcal {C}_{ab}$
then we have
$C\in \mathcal {C}_{ab}$
then we have
![]() $c,c'\in S$
with
$c,c'\in S$
with
![]() $C\ni c<_{c'}ab$
. In particular,
$C\ni c<_{c'}ab$
. In particular,
![]() $abc'\in Z$
and
$abc'\in Z$
and
![]() $abc'c=c$
and hence
$abc'c=c$
and hence
![]() $bc'|C$
, by (8-2). By Proposition 7.7,
$bc'|C$
, by (8-2). By Proposition 7.7,
![]() $B=(bc'C)^<$
is a coset with
$B=(bc'C)^<$
is a coset with
![]() $\mathsf {s}(B)=\mathsf {s}(C)$
. Also
$\mathsf {s}(B)=\mathsf {s}(C)$
. Also
![]() $B\in \mathcal {C}_{bc'c}\subseteq \mathcal {C}_b$
, by (8-3), as
$B\in \mathcal {C}_{bc'c}\subseteq \mathcal {C}_b$
, by (8-3), as
![]() $c'c\in N$
. As
$c'c\in N$
. As
![]() $b\in B$
, we have
$b\in B$
, we have
![]() $b'\in B^*$
with
$b'\in B^*$
with
![]() $bb'\in Z\subseteq N$
and hence
$bb'\in Z\subseteq N$
and hence
![]() $C\cdot B^*\in \mathcal {C}_{ab}\cdot \mathcal {C}_{b'}\subseteq \mathcal {C}_{abb'}\subseteq \mathcal {C}_a$
, again by (8-3). Thus,
$C\cdot B^*\in \mathcal {C}_{ab}\cdot \mathcal {C}_{b'}\subseteq \mathcal {C}_{abb'}\subseteq \mathcal {C}_a$
, again by (8-3). Thus,
![]() $C=C\cdot B^*\cdot B\in \mathcal {C}_a\cdot \mathcal {C}_b$
. This shows that
$C=C\cdot B^*\cdot B\in \mathcal {C}_a\cdot \mathcal {C}_b$
. This shows that
![]() $\mathcal {C}_{ab}=\mathcal {C}_a\cdot \mathcal {C}_b$
, for all
$\mathcal {C}_{ab}=\mathcal {C}_a\cdot \mathcal {C}_b$
, for all
![]() $a,b\in S$
, so
$a,b\in S$
, so
![]() $\mathcal {C}$
is indeed a semigroup homomorphism.
$\mathcal {C}$
is indeed a semigroup homomorphism.
To see that
![]() $\mathcal {C}$
is even an étale representation, note first that
$\mathcal {C}$
is even an étale representation, note first that
![]() $n\in N$
implies that
$n\in N$
implies that
![]() $\mathcal {C}_n$
consists entirely of unit cosets, thanks to Proposition 8.2. Also any coset C must satisfy
$\mathcal {C}_n$
consists entirely of unit cosets, thanks to Proposition 8.2. Also any coset C must satisfy
![]() $C\subseteq C^<$
by definition, so if
$C\subseteq C^<$
by definition, so if
![]() $C\in \mathcal {C}_a$
then we have
$C\in \mathcal {C}_a$
then we have
![]() $b\in C$
with
$b\in C$
with
![]() $b<a$
and hence
$b<a$
and hence
![]() $C\in \mathcal {C}_b$
, that is, (Locally Round) is also satisfied. As each
$C\in \mathcal {C}_b$
, that is, (Locally Round) is also satisfied. As each
![]() $C\in \mathcal {C}(S)$
is nonempty, we have
$C\in \mathcal {C}(S)$
is nonempty, we have
![]() $a\in C$
and hence
$a\in C$
and hence
![]() $C\in \mathcal {C}_a$
, that is,
$C\in \mathcal {C}_a$
, that is,
![]() $(\mathcal {C}_a)_{a\in S}$
covers
$(\mathcal {C}_a)_{a\in S}$
covers
![]() $\mathcal {C}(S)$
, as required.
$\mathcal {C}(S)$
, as required.
To see that
![]() $\mathcal {C}$
is universal, take any other étale representation
$\mathcal {C}$
is universal, take any other étale representation
![]() $\theta :S\rightarrow \mathcal {B}(G)$
. For each
$\theta :S\rightarrow \mathcal {B}(G)$
. For each
![]() $g\in G$
, define
$g\in G$
, define
![]() $\phi (g)\subseteq S$
by
$\phi (g)\subseteq S$
by
We claim that
![]() $\phi (g)\in \mathcal {C}(S)$
. Certainly
$\phi (g)\in \mathcal {C}(S)$
. Certainly
![]() $\phi (g)\neq \emptyset $
, as
$\phi (g)\neq \emptyset $
, as
![]() $\theta [S]$
covers G. Also
$\theta [S]$
covers G. Also
![]() $\phi (g)\subseteq \phi (g)^<$
, as
$\phi (g)\subseteq \phi (g)^<$
, as
![]() $\theta $
is required to satisfy (Locally Round). Conversely, suppose that
$\theta $
is required to satisfy (Locally Round). Conversely, suppose that
![]() $\phi (g)\ni a<b$
so
$\phi (g)\ni a<b$
so
![]() $g\in \theta (a)=\theta (asb)=\theta (a)\theta (s)\theta (b)$
and
$g\in \theta (a)=\theta (asb)=\theta (a)\theta (s)\theta (b)$
and
![]() $\theta (a)\theta (s)=\theta (as)\in \theta [N]\subseteq \mathcal {O}(G^0)$
. Arguing as in the proof of Proposition 5.2 (or considering the special case of Proposition 5.2 where
$\theta (a)\theta (s)=\theta (as)\in \theta [N]\subseteq \mathcal {O}(G^0)$
. Arguing as in the proof of Proposition 5.2 (or considering the special case of Proposition 5.2 where
![]() $\pi :G\rightarrow G$
is the identity bundle and hence
$\pi :G\rightarrow G$
is the identity bundle and hence
![]() $\mathcal {B}(G)\approx \mathcal {S}(\pi )$
), it follows that
$\mathcal {B}(G)\approx \mathcal {S}(\pi )$
), it follows that
![]() $g\in \theta (b)$
and hence
$g\in \theta (b)$
and hence
![]() $b\in \phi (g)$
, showing that
$b\in \phi (g)$
, showing that
![]() $\phi (g)^<\subseteq \phi (g)$
. Finally, note that if
$\phi (g)^<\subseteq \phi (g)$
. Finally, note that if
![]() $b\in \phi (g)^*$
then
$b\in \phi (g)^*$
then
![]() $a<_bc$
, for some
$a<_bc$
, for some
![]() $a\in \phi (g)$
, which means that
$a\in \phi (g)$
, which means that
![]() $g\in \theta (a)$
and hence
$g\in \theta (a)$
and hence
![]() $g^{-1}\in \theta (b)$
, again by Proposition 5.2. This shows that
$g^{-1}\in \theta (b)$
, again by Proposition 5.2. This shows that
![]() $\phi (g)^*\subseteq \phi (g^{-1})$
so, for any
$\phi (g)^*\subseteq \phi (g^{-1})$
so, for any
![]() $a,c\in \phi (g)$
and
$a,c\in \phi (g)$
and
![]() $b\in \phi (g)^*$
, we see that
$b\in \phi (g)^*$
, we see that
![]() $g=gg^{-1}g\in \theta (a)\theta (b)\theta (c)=\theta (abc)$
, that is,
$g=gg^{-1}g\in \theta (a)\theta (b)\theta (c)=\theta (abc)$
, that is,
![]() $abc\in \phi (g)$
. Thus, we have shown that
$abc\in \phi (g)$
. Thus, we have shown that
![]() $\phi (g)$
is a nonempty coset, proving the claim.
$\phi (g)$
is a nonempty coset, proving the claim.
Now
![]() $\phi (g)^*\subseteq \phi (g^{-1})=\phi (g^{-1})^{**}\subseteq \phi (g)^*$
, that is,
$\phi (g)^*\subseteq \phi (g^{-1})=\phi (g^{-1})^{**}\subseteq \phi (g)^*$
, that is,
![]() $\phi (g)^*=\phi (g^{-1})$
. Also
$\phi (g)^*=\phi (g^{-1})$
. Also
As
![]() $\phi (\mathsf {r}(g))$
contains a unit coset and hence an element of N,
$\phi (\mathsf {r}(g))$
contains a unit coset and hence an element of N,
![]() $\phi (\mathsf {r}(g))$
is also a unit coset. Taking any
$\phi (\mathsf {r}(g))$
is also a unit coset. Taking any
![]() $a\in \phi (g)$
and
$a\in \phi (g)$
and
![]() $a'\in \phi (g^{-1})$
, we see that
$a'\in \phi (g^{-1})$
, we see that
![]() $\mathsf {r}(g)=gg^{-1}\in \theta (a)\theta (a')=\theta (aa')$
. Thus,
$\mathsf {r}(g)=gg^{-1}\in \theta (a)\theta (a')=\theta (aa')$
. Thus,
![]() $aa'\in \phi (\mathsf {r}(g))$
and then (6-4) and (7-2) yield
$aa'\in \phi (\mathsf {r}(g))$
and then (6-4) and (7-2) yield
Likewise,
![]() $\mathsf {s}(\phi (g))=\phi (\mathsf {s}(g))$
. If we have another
$\mathsf {s}(\phi (g))=\phi (\mathsf {s}(g))$
. If we have another
![]() $h\in G$
with
$h\in G$
with
![]() $\mathsf {s}(g)=\mathsf {r}(h)$
then
$\mathsf {s}(g)=\mathsf {r}(h)$
then
so
![]() $\phi (g)\cdot \phi (h)$
is defined and
$\phi (g)\cdot \phi (h)$
is defined and
Likewise,
![]() $\phi (gh)\cdot \phi (h^{-1})\subseteq \phi (ghh^{-1})=\phi (g)$
and hence
$\phi (gh)\cdot \phi (h^{-1})\subseteq \phi (ghh^{-1})=\phi (g)$
and hence
This shows that
![]() $\phi (gh)=\phi (g)\cdot \phi (h)$
and hence
$\phi (gh)=\phi (g)\cdot \phi (h)$
and hence
![]() $\phi $
is a functor.
$\phi $
is a functor.
Now suppose that
![]() $x\in G^0$
,
$x\in G^0$
,
![]() $C\in \mathcal {C}(S)$
and
$C\in \mathcal {C}(S)$
and
![]() $\mathsf {r}(C)=\phi (x)$
. Taking any
$\mathsf {r}(C)=\phi (x)$
. Taking any
![]() $c\in C$
and
$c\in C$
and
![]() $c'\in C^*$
, we see that
$c'\in C^*$
, we see that
![]() $cc'\in CC^*\subseteq \mathsf {r}(C)=\phi (x)$
, so
$cc'\in CC^*\subseteq \mathsf {r}(C)=\phi (x)$
, so
![]() $x\in \theta (cc')=\theta (c)\theta (c')$
and hence
$x\in \theta (cc')=\theta (c)\theta (c')$
and hence
![]() $x=\mathsf {r}(g)$
, for some
$x=\mathsf {r}(g)$
, for some
![]() $g\in \theta (c)\cap \theta (c')^{-1}$
. Then (6-4) and (7-2) again yield
$g\in \theta (c)\cap \theta (c')^{-1}$
. Then (6-4) and (7-2) again yield
This shows that
![]() $\phi $
is star-surjective. To see that
$\phi $
is star-surjective. To see that
![]() $\phi $
is also star-injective, just note that
$\phi $
is also star-injective, just note that
![]() $\mathsf {r}(g)=\mathsf {r}(h)$
and
$\mathsf {r}(g)=\mathsf {r}(h)$
and
![]() $\phi (g)=\phi (h)$
, or even just
$\phi (g)=\phi (h)$
, or even just
![]() $\phi (g)\cap \phi (h)\neq \emptyset $
, implies
$\phi (g)\cap \phi (h)\neq \emptyset $
, implies
![]() $g=h$
, as
$g=h$
, as
![]() $a\in \phi (g)\cap \phi (h)$
implies that g and h are in the same slice
$a\in \phi (g)\cap \phi (h)$
implies that g and h are in the same slice
![]() $\theta (a)$
.
$\theta (a)$
.
Now note that, for any
![]() $a\in S$
,
$a\in S$
,
![]() $\phi ^{-1}[\mathcal {C}_a]=\theta (a)\in \mathcal {B}(G)$
because
$\phi ^{-1}[\mathcal {C}_a]=\theta (a)\in \mathcal {B}(G)$
because
Thus,
![]() $\phi $
is an étale morphism from G to
$\phi $
is an étale morphism from G to
![]() $\mathcal {C}(S)$
with
$\mathcal {C}(S)$
with
![]() $\theta =\overline \phi \circ \mathcal {C}$
.
$\theta =\overline \phi \circ \mathcal {C}$
.
Finally, for uniqueness, suppose that we had another map
![]() $\psi :G\rightarrow \mathcal {C}(S)$
such that
$\psi :G\rightarrow \mathcal {C}(S)$
such that
![]() $\overline \psi \circ \mathcal {C}=\theta $
, that is,
$\overline \psi \circ \mathcal {C}=\theta $
, that is,
![]() $\psi ^{-1}[\mathcal {C}_a]=\theta (a)$
, for all
$\psi ^{-1}[\mathcal {C}_a]=\theta (a)$
, for all
![]() $a\in S$
. Then again we see that
$a\in S$
. Then again we see that
![]() $g\in \theta (a)$
if and only if
$g\in \theta (a)$
if and only if
![]() $\psi (g)\in \mathcal {C}_a$
if and only if
$\psi (g)\in \mathcal {C}_a$
if and only if
![]() $a\in \psi (g)$
and hence
$a\in \psi (g)$
and hence
![]() $\psi (g)=\{a\in S:g\in \theta (a)\}=\phi (g)$
, for all
$\psi (g)=\{a\in S:g\in \theta (a)\}=\phi (g)$
, for all
![]() $g\in G$
.
$g\in G$
.
Remark 8.12. If the subbasic slices of a groupoid are closed under pointwise products then the same is true of arbitrary open slices; see the proof of [Reference Bice and Starling6, Proposition 3.18]. In particular, this applies to
![]() $\mathcal {C}(S)$
if
$\mathcal {C}(S)$
if
![]() $\mathcal {C}$
is a semigroup homomorphism, as shown in the first part of the proof above. As
$\mathcal {C}$
is a semigroup homomorphism, as shown in the first part of the proof above. As
![]() $C\mapsto C^*$
is immediately seen to be continuous on
$C\mapsto C^*$
is immediately seen to be continuous on
![]() $\mathcal {C}(S)$
, as mentioned at the start of the proof of Theorem 8.4, the open slices of
$\mathcal {C}(S)$
, as mentioned at the start of the proof of Theorem 8.4, the open slices of
![]() $\mathcal {C}(S)$
are also closed under pointwise inverses. It follows that
$\mathcal {C}(S)$
are also closed under pointwise inverses. It follows that
![]() $\mathcal {C}(S)$
is étale, again by [Reference Bice and Starling6, Proposition 3.18], which provides an alternative proof of Theorem 8.4 in the symmetric case.
$\mathcal {C}(S)$
is étale, again by [Reference Bice and Starling6, Proposition 3.18], which provides an alternative proof of Theorem 8.4 in the symmetric case.
While the coset representation
![]() $\mathcal {C}$
is universal, it can only be faithful when N consists entirely of idempotents. If we want faithful representations of more general structured semigroups, including those with few idempotents, then we need to consider finer representations on groupoid bundles. In particular, to construct such a bundle over the coset groupoid, we split up the cosets into equivalence classes with respect to certain relations that we now proceed to examine.
$\mathcal {C}$
is universal, it can only be faithful when N consists entirely of idempotents. If we want faithful representations of more general structured semigroups, including those with few idempotents, then we need to consider finer representations on groupoid bundles. In particular, to construct such a bundle over the coset groupoid, we split up the cosets into equivalence classes with respect to certain relations that we now proceed to examine.
9 Equivalence
Definition 9.1. For any
![]() $A\subseteq S$
, we define a relation
$A\subseteq S$
, we define a relation
![]() $\sim _A$
on
$\sim _A$
on
![]() $A^<$
by
$A^<$
by
Here A will usually be an atlas, in which case
![]() $A^<$
is a coset.
$A^<$
is a coset.
We think of
![]() $a\sim _Ab$
as saying that a and b have the same ‘germ’ at A.
$a\sim _Ab$
as saying that a and b have the same ‘germ’ at A.
Example 9.2. Suppose that
![]() $S=N=Z=C_0(X)$
are continuous functions from X to
$S=N=Z=C_0(X)$
are continuous functions from X to
![]() $\mathbb {C}$
vanishing at infinity, where X is a locally compact Hausdorff space. Then each
$\mathbb {C}$
vanishing at infinity, where X is a locally compact Hausdorff space. Then each
![]() $x\in X$
defines a coset (in fact an ultrafilter)
$x\in X$
defines a coset (in fact an ultrafilter)
(note that this is consistent with (3-2) when we identify each
![]() $a\in S$
with the restriction to its support
$a\in S$
with the restriction to its support
![]() $a|_{\mathrm {supp}(a)}$
). Moreover, for all
$a|_{\mathrm {supp}(a)}$
). Moreover, for all
![]() $a,b\in S_x$
,
$a,b\in S_x$
,
Indeed, if
![]() $a\sim _{S_x}b$
, that is,
$a\sim _{S_x}b$
, that is,
![]() $sat=sbt$
, for some
$sat=sbt$
, for some
![]() $s,t\in S_x^*=S_x$
, then
$s,t\in S_x^*=S_x$
, then
![]() $a(x)=b(x)$
, for all
$a(x)=b(x)$
, for all
![]() $x\in \mathrm {supp}(s)\cap \mathrm {supp}(t)$
. Conversely, if
$x\in \mathrm {supp}(s)\cap \mathrm {supp}(t)$
. Conversely, if
![]() $a(y)=b(y)$
for all y in a neighbourhood N of x then, taking any
$a(y)=b(y)$
for all y in a neighbourhood N of x then, taking any
![]() $s\in S_x$
with
$s\in S_x$
with
![]() $\mathrm {supp}(s)\subseteq N$
, we see that
$\mathrm {supp}(s)\subseteq N$
, we see that
![]() $sas=sbs$
so
$sas=sbs$
so
![]() $a\sim _{S_x}b$
.
$a\sim _{S_x}b$
.
Another example to think of would be inverse semigroups, where
![]() $a\sim _Ab$
is just saying that a and b have a common lower bound in A. We prove something similar for more general semigroups in (9-4) below by considering the subsets
$a\sim _Ab$
is just saying that a and b have a common lower bound in A. We prove something similar for more general semigroups in (9-4) below by considering the subsets
 $$ \begin{align*} A^Z&=\{z\in Z:\text{ there exists } a\in A\ (az=a)\},\\ {}^Z\!A&=\{z\in Z:\text{ there exists } a\in A\ (za=a))\}. \end{align*} $$
$$ \begin{align*} A^Z&=\{z\in Z:\text{ there exists } a\in A\ (az=a)\},\\ {}^Z\!A&=\{z\in Z:\text{ there exists } a\in A\ (za=a))\}. \end{align*} $$
First, however, we need to examine their basic properties.
Proposition 9.3. If A is an atlas then
![]() $A^Z$
is a subsemigroup of Z and
$A^Z$
is a subsemigroup of Z and
Proof. If
![]() $y,z\in A^Z$
then we have
$y,z\in A^Z$
then we have
![]() $a,b\in A$
with
$a,b\in A$
with
![]() $ay=a$
and
$ay=a$
and
![]() $bz=b$
. As A is an atlas,
$bz=b$
. As A is an atlas,
![]() $A\subseteq A^<$
, so we have
$A\subseteq A^<$
, so we have
![]() $a',a''\in S$
with
$a',a''\in S$
with
![]() $A\ni a''<_{a'}a$
. Then
$A\ni a''<_{a'}a$
. Then
![]() $ba'a\in AA^*A\subseteq A$
and, moreover,
$ba'a\in AA^*A\subseteq A$
and, moreover,
![]() $ba'ayz=ba'az=bza'a=ba'a$
. Thus,
$ba'ayz=ba'az=bza'a=ba'a$
. Thus,
![]() $yz\in A^Z$
, which shows that
$yz\in A^Z$
, which shows that
![]() $A^Z$
is a subsemigroup of Z. A dual argument works for
$A^Z$
is a subsemigroup of Z. A dual argument works for
![]() ${}^Z\!A$
.
${}^Z\!A$
.
(9-1) If
 $z\in A^{*Z}$
then we have
$z\in A^{*Z}$
then we have
 $a,a',a''\in S$
with
$a,a',a''\in S$
with
 $A\ni a''<_{a'}a$
and
$A\ni a''<_{a'}a$
and
 $a'z=a'$
and hence
$a'z=a'$
and hence
 $za''=za''a'a=a''a'za=a''a'a=a''$
, showing that
$za''=za''a'a=a''a'za=a''a'a=a''$
, showing that
 $z\in {}^Z\!A$
. Conversely, if
$z\in {}^Z\!A$
. Conversely, if
 $z\in {}^Z\!A$
, then we have
$z\in {}^Z\!A$
, then we have
 $a\in A$
with
$a\in A$
with
 $za=a$
. As
$za=a$
. As
 $A\subseteq A^<$
, we have
$A\subseteq A^<$
, we have
 $a',a''\in S$
with
$a',a''\in S$
with
 $A\ni a''<_{a'}a$
and hence
$A\ni a''<_{a'}a$
and hence
 $a'aa'z=a'zaa'=a'aa'\in A^*AA^*\subseteq A^*$
, showing that
$a'aa'z=a'zaa'=a'aa'\in A^*AA^*\subseteq A^*$
, showing that
 $z\in A^{*Z}$
. Thus,
$z\in A^{*Z}$
. Thus,
 ${}^Z\!A=A^{*Z}$
and, likewise,
${}^Z\!A=A^{*Z}$
and, likewise,
 ${}^Z(A^*)=A^Z$
. Then (6-4) yields
${}^Z(A^*)=A^Z$
. Then (6-4) yields
 $A^{<Z}=A^{**Z}={}^Z(A^*)=A^Z$
.
$A^{<Z}=A^{**Z}={}^Z(A^*)=A^Z$
.Now if
 $z\in A^Z$
then we have
$z\in A^Z$
then we have
 $a\in A$
with
$a\in A$
with
 $az=a$
. Taking
$az=a$
. Taking
 $a',a''\in A$
with
$a',a''\in A$
with
 $A\ni a''<_{a'}a$
, we see that
$A\ni a''<_{a'}a$
, we see that
 $A^Z\ni a'a=a'az$
, so
$A^Z\ni a'a=a'az$
, so
 $z\in (A^Z)^Z$
, and
$z\in (A^Z)^Z$
, and
 $a'a<_zz$
, so
$a'a<_zz$
, so
 $z\in (A^*A)^<=\mathsf {s}(A)$
. This shows that
$z\in (A^*A)^<=\mathsf {s}(A)$
. This shows that
 $A^Z\subseteq \mathsf {s}(A)$
and
$A^Z\subseteq \mathsf {s}(A)$
and
 $A^Z\subseteq (A^Z)^Z\subseteq \mathsf {s}(A)^Z$
. Conversely, if
$A^Z\subseteq (A^Z)^Z\subseteq \mathsf {s}(A)^Z$
. Conversely, if
 $z\in \mathsf {s}(A)^Z$
then we have
$z\in \mathsf {s}(A)^Z$
then we have
 $b\in \mathsf {s}(A)$
with
$b\in \mathsf {s}(A)$
with
 $bz=b$
. Taking
$bz=b$
. Taking
 $a\in A$
, note that
$a\in A$
, note that
 $abz=ab\in A\mathsf {s}(A)\subseteq A^<$
so
$abz=ab\in A\mathsf {s}(A)\subseteq A^<$
so
 $z\in A^{<Z}=A^Z$
, showing that
$z\in A^{<Z}=A^Z$
, showing that
 $\mathsf {s}(A)^Z\subseteq A^Z$
.
$\mathsf {s}(A)^Z\subseteq A^Z$
.(9-2) If
 $A\ni a''<_{a'}a$
and
$A\ni a''<_{a'}a$
and
 $zb=b\in A$
then we have
$zb=b\in A$
then we have
 $b',b''\in S$
with
$b',b''\in S$
with
 $A\ni b''<_{b'}b$
and hence
$A\ni b''<_{b'}b$
and hence
 $bb'a''\in AA^*A\subseteq A$
and
$bb'a''\in AA^*A\subseteq A$
and
 $bb'a''a'za=zbb'a''a'a=bb'a''$
, that is,
$bb'a''a'za=zbb'a''a'a=bb'a''$
, that is,
 $bb'a''$
witnesses
$bb'a''$
witnesses
 $a'za\in A^Z$
.
$a'za\in A^Z$
.(9-3) If
 $A\ni a<_{a'}a''$
and
$A\ni a<_{a'}a''$
and
 $z\in {}^Z\!A$
then (9-2) yields
$z\in {}^Z\!A$
then (9-2) yields
 $a'za''\in A^Z$
and hence
$a'za''\in A^Z$
and hence
 $za=zaa'a''=aa'za''\in aA^Z$
.
$za=zaa'a''=aa'za''\in aA^Z$
.
Dually to (9-2),
![]() $A\ni a''<_{a'}a$
also implies
$A\ni a''<_{a'}a$
also implies
![]() $aA^Za'\subseteq {}^Z\!A$
.
$aA^Za'\subseteq {}^Z\!A$
.
Proposition 9.4. If
![]() $A\subseteq S$
is an atlas and
$A\subseteq S$
is an atlas and
![]() $a,b\in A^<$
then
$a,b\in A^<$
then
Proof. Take
![]() $a,b\in A^<$
. If
$a,b\in A^<$
. If
![]() $s\in A^*$
and
$s\in A^*$
and
![]() $sa=sb$
or
$sa=sb$
or
![]() $as=bs$
then
$as=bs$
then
![]() $sas=sbs$
so
$sas=sbs$
so
![]() $a\sim _Ab$
. This proves the last
$a\sim _Ab$
. This proves the last
![]() $\Leftarrow $
.
$\Leftarrow $
.
If
![]() $a\sim _Ab$
then we have
$a\sim _Ab$
then we have
![]() $s,t\in A^*$
with
$s,t\in A^*$
with
![]() $sat=sbt$
. Taking any
$sat=sbt$
. Taking any
![]() $s',s'',t',t''\in S$
with
$s',s'',t',t''\in S$
with
![]() $A^*\ni s''<_{s'}s$
and
$A^*\ni s''<_{s'}s$
and
![]() $A^*\ni t''<_{t'}t$
, we see that
$A^*\ni t''<_{t'}t$
, we see that
![]() ${}^Z\!AaA^Z\ni s'satt'=s'sbtt'\in {}^Z\!AbA^Z$
. This proves the first
${}^Z\!AaA^Z\ni s'satt'=s'sbtt'\in {}^Z\!AbA^Z$
. This proves the first
![]() $\Rightarrow $
.
$\Rightarrow $
.
Conversely, assume that
![]() ${}^Z\!AaA^Z\cap {}^Z\!AbA^Z\neq \emptyset $
. First, we claim that
${}^Z\!AaA^Z\cap {}^Z\!AbA^Z\neq \emptyset $
. First, we claim that
![]() $aA^Z\cap bA^Z\neq \emptyset $
. To see this, take
$aA^Z\cap bA^Z\neq \emptyset $
. To see this, take
![]() $w,x\in {}^Z\!A$
and
$w,x\in {}^Z\!A$
and
![]() $y,z\in A^Z$
with
$y,z\in A^Z$
with
![]() $way=xbz$
. As
$way=xbz$
. As
![]() $a\in A^<$
, we have
$a\in A^<$
, we have
![]() $a',a''\in S$
with
$a',a''\in S$
with
![]() $A\ni a''<_{a'}a$
. Note that
$A\ni a''<_{a'}a$
. Note that
![]() $waya'a=waa'ay=aa'way\in aa'{}^Z\!AaA^Z\subseteq aA^Z$
by Proposition 9.3. Likewise, as
$waya'a=waa'ay=aa'way\in aa'{}^Z\!AaA^Z\subseteq aA^Z$
by Proposition 9.3. Likewise, as
![]() $b\in A^<$
, we have
$b\in A^<$
, we have
![]() $b',b''\in S$
with
$b',b''\in S$
with
![]() $A\ni b''<_{b'}b$
and then
$A\ni b''<_{b'}b$
and then
![]() $xbzb'b\in bA^Z$
. As
$xbzb'b\in bA^Z$
. As
![]() $way=xbz$
,
$way=xbz$
,
This proves the claim.
Next, we claim that we have
![]() $t\in A^*$
with
$t\in A^*$
with
![]() $at=bt\in {}^Z\!A$
and
$at=bt\in {}^Z\!A$
and
![]() $ta\in A^Z$
. To see this, take
$ta\in A^Z$
. To see this, take
![]() $p,q\in A^Z$
with
$p,q\in A^Z$
with
![]() $ap=bq$
. As
$ap=bq$
. As
![]() $p\in A^Z$
, we have
$p\in A^Z$
, we have
![]() $c\in A\subseteq A^<$
with
$c\in A\subseteq A^<$
with
![]() $cp=c$
and
$cp=c$
and
![]() $c',c''\in S$
with
$c',c''\in S$
with
![]() $A\ni c''<_{c'}c$
. Likewise, we have
$A\ni c''<_{c'}c$
. Likewise, we have
![]() $d,d',d''\in S$
with
$d,d',d''\in S$
with
![]() $A\ni d''<_{d'}d$
and
$A\ni d''<_{d'}d$
and
![]() $dq=d$
. Let
$dq=d$
. Let
![]() $z=c'cd'd=d'dc'c\in A^Z\cap A^*A$
by Proposition 9.3. Now just note that
$z=c'cd'd=d'dc'c\in A^Z\cap A^*A$
by Proposition 9.3. Now just note that
![]() $az=ac'cd'd=ac'cpd'd=apc'cd'd=apz$
and, likewise,
$az=ac'cd'd=ac'cpd'd=apc'cd'd=apz$
and, likewise,
Taking the
![]() $a'$
above, note that
$a'$
above, note that
![]() $t=za'\in A^*AA^*\subseteq A^*$
,
$t=za'\in A^*AA^*\subseteq A^*$
,
![]() $ta=za'a\in A^ZA^Z\subseteq A^Z$
and
$ta=za'a\in A^ZA^Z\subseteq A^Z$
and
![]() $bza'=aza'\in aA^Za'\subseteq {}^Z\!A$
by Proposition 9.3, proving the claim.
$bza'=aza'\in aA^Za'\subseteq {}^Z\!A$
by Proposition 9.3, proving the claim.
Likewise, we have
![]() $u\in A^*$
with
$u\in A^*$
with
![]() $ua=ub\in A^Z$
and
$ua=ub\in A^Z$
and
![]() $au\in {}^Z\!A$
. Again Proposition 9.3 yields
$au\in {}^Z\!A$
. Again Proposition 9.3 yields
![]() $taub=taua\in A^ZA^Z\subseteq A^Z$
and
$taub=taua\in A^ZA^Z\subseteq A^Z$
and
![]() $btau=atau\in A^ZA^Z\subseteq A^Z$
, that is,
$btau=atau\in A^ZA^Z\subseteq A^Z$
, that is,
for
![]() $s=tau$
. This completes the cycle of equivalences.
$s=tau$
. This completes the cycle of equivalences.
One could also write down other characterisations of
![]() $\sim _A$
that lie somewhere in between (9-4) and (9-5). One could also replace
$\sim _A$
that lie somewhere in between (9-4) and (9-5). One could also replace
![]() $A^*$
with some coinitial subset
$A^*$
with some coinitial subset
![]() $A'$
. That is to say, if A is an atlas and
$A'$
. That is to say, if A is an atlas and
![]() $A'\subseteq A^*=(A')^<$
then, for example,
$A'\subseteq A^*=(A')^<$
then, for example,
Indeed, if we have
![]() $s\in A'\subseteq A^*$
with
$s\in A'\subseteq A^*$
with
![]() $as=bs$
then
$as=bs$
then
![]() $aA^Z\cap bA^Z\neq \emptyset $
and so certainly
$aA^Z\cap bA^Z\neq \emptyset $
and so certainly
![]() ${}^Z\!AaA^Z\cap {}^Z\!AbA^Z\neq \emptyset $
and hence
${}^Z\!AaA^Z\cap {}^Z\!AbA^Z\neq \emptyset $
and hence
![]() $a\sim _Ab$
, by (9-4). Conversely, if
$a\sim _Ab$
, by (9-4). Conversely, if
![]() $a\sim _Ab$
then we have
$a\sim _Ab$
then we have
![]() $s\in A^*$
with
$s\in A^*$
with
![]() $as=bs$
by (9-5). If
$as=bs$
by (9-5). If
![]() $A^*=(A')^<$
too then we have
$A^*=(A')^<$
too then we have
![]() $a',t\in S$
with
$a',t\in S$
with
![]() $A'\ni a'<_ts$
and hence
$A'\ni a'<_ts$
and hence
![]() $aa'=asta'=bsta'=ba'$
, proving (9-6).
$aa'=asta'=bsta'=ba'$
, proving (9-6).
We can now finally show that
![]() $\sim _A$
is an equivalence relation.
$\sim _A$
is an equivalence relation.
Corollary 9.5. If
![]() $A\subseteq S$
is an atlas then
$A\subseteq S$
is an atlas then
![]() $\sim _A$
is an equivalence relation.
$\sim _A$
is an equivalence relation.
Proof. We immediately see that
![]() $\sim _A$
is a reflexive and symmetric relation on
$\sim _A$
is a reflexive and symmetric relation on
![]() $A^<$
. On the other hand, if
$A^<$
. On the other hand, if
![]() $a\sim _Ab\sim _Ac$
then we have
$a\sim _Ab\sim _Ac$
then we have
![]() $s,t\in A^*$
with
$s,t\in A^*$
with
![]() $sa=sb$
and
$sa=sb$
and
![]() $bt=ct$
by (9-5). Thus,
$bt=ct$
by (9-5). Thus,
![]() $sat=sbt=sct$
, showing that
$sat=sbt=sct$
, showing that
![]() $a\sim _Ac$
. So
$a\sim _Ac$
. So
![]() $\sim _A$
is also transitive and hence an equivalence relation on
$\sim _A$
is also transitive and hence an equivalence relation on
![]() $A^<$
.
$A^<$
.
Also, multiples of
![]() ${}^Z\!A$
and
${}^Z\!A$
and
![]() $A^Z$
do not change the equivalence class.
$A^Z$
do not change the equivalence class.
Corollary 9.6. For any atlas
![]() $A\subseteq S$
,
$A\subseteq S$
,
![]() $y\in {}^Z\!A$
,
$y\in {}^Z\!A$
,
![]() $z\in A^Z$
and
$z\in A^Z$
and
![]() $a\in A^<$
,
$a\in A^<$
,
Moreover, these equivalence relations even respect products.
Corollary 9.7. If
![]() $A,B\subseteq S$
are atlases with
$A,B\subseteq S$
are atlases with
![]() $\mathsf {s}(A)=\mathsf {r}(B)$
then
$\mathsf {s}(A)=\mathsf {r}(B)$
then
10 Bundles
In the present section we show that the equivalence classes of the previous section form an étale bundle over the coset groupoid. Firstly, if
![]() $A\subseteq S$
is an atlas and
$A\subseteq S$
is an atlas and
![]() $a\in A^<$
, we define
$a\in A^<$
, we define
![]() $[a,A]$
to be the pair consisting of the
$[a,A]$
to be the pair consisting of the
![]() $\sim _A$
-equivalence class of a together with the coset
$\sim _A$
-equivalence class of a together with the coset
![]() $A^<$
generated by A, that is,
$A^<$
generated by A, that is,
We denote the set of all such pairs by
 $$ \begin{align*} \widetilde{\mathcal{C}}(S)=\{[c,C]:c\in C\in\mathcal{C}(S)\}. \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{C}}(S)=\{[c,C]:c\in C\in\mathcal{C}(S)\}. \end{align*} $$
Proposition 10.1.
 $\widetilde {\mathcal {C}}(S)$
is a groupoid under the product
$\widetilde {\mathcal {C}}(S)$
is a groupoid under the product
where
![]() $[c,C]^{-1}=[c',C^*]$
, for any
$[c,C]^{-1}=[c',C^*]$
, for any
![]() $c'$
with
$c'$
with
![]() $C\ni d<_{c'}c$
.
$C\ni d<_{c'}c$
.
Proof. By (9-8), the product is well defined. Also, as S is a semigroup and
![]() $\mathcal {C}(S)$
is a groupoid,
$\mathcal {C}(S)$
is a groupoid,
 $\widetilde {\mathcal {C}}(S)$
can be viewed as a semicategory with unit cosets as objects. To show that
$\widetilde {\mathcal {C}}(S)$
can be viewed as a semicategory with unit cosets as objects. To show that
 $\widetilde {C}(S)$
is a category we must find a unit
$\widetilde {C}(S)$
is a category we must find a unit
 $[z,U]\in \widetilde {\mathcal {C}}(S)$
for every unit
$[z,U]\in \widetilde {\mathcal {C}}(S)$
for every unit
![]() $U\in \mathcal {C}(S)$
.
$U\in \mathcal {C}(S)$
.
We claim that
 $[z,U]\in \widetilde {\mathcal {C}}(S)$
is a unit, for any
$[z,U]\in \widetilde {\mathcal {C}}(S)$
is a unit, for any
![]() $z\in U^Z=U^{*Z}={}^ZU$
, by (9-1). Indeed, if
$z\in U^Z=U^{*Z}={}^ZU$
, by (9-1). Indeed, if
![]() $C\in \mathcal {C}(S)$
and
$C\in \mathcal {C}(S)$
and
![]() $\mathsf {s}(C)=U$
then
$\mathsf {s}(C)=U$
then
![]() $C^Z=U^Z$
by (9-1). For any
$C^Z=U^Z$
by (9-1). For any
![]() $c\in C$
, this means that
$c\in C$
, this means that
![]() $cz\sim _Cc$
so
$cz\sim _Cc$
so
![]() $[c,C][z,U]=[cz,CU]=[c,C]$
. Likewise, if
$[c,C][z,U]=[cz,CU]=[c,C]$
. Likewise, if
![]() $\mathsf {r}(C)=U$
then
$\mathsf {r}(C)=U$
then
![]() ${}^ZC={}^ZU$
so
${}^ZC={}^ZU$
so
![]() $[z,U][c,C]=[zc,UC]=[c,C]$
, proving the claim. Thus,
$[z,U][c,C]=[zc,UC]=[c,C]$
, proving the claim. Thus,
 $\widetilde {\mathcal {C}}(S)$
is a category.
$\widetilde {\mathcal {C}}(S)$
is a category.
Next note that, for any
![]() $c\in C$
, we have
$c\in C$
, we have
![]() $c',d\in S$
with
$c',d\in S$
with
![]() $C\ni d<_{c'}c$
and then
$C\ni d<_{c'}c$
and then
![]() $[c',C^*][c,C]=[c'c,\mathsf {s}(C)]$
and
$[c',C^*][c,C]=[c'c,\mathsf {s}(C)]$
and
![]() $[c,C][c',C^*]=[cc',\mathsf {r}(C)]$
. As
$[c,C][c',C^*]=[cc',\mathsf {r}(C)]$
. As
![]() $c'c\in C^Z=\mathsf {s}(C)^Z$
and
$c'c\in C^Z=\mathsf {s}(C)^Z$
and
![]() $cc'\in {}^ZC={}^Z\mathsf {r}(C)$
, these are both units in
$cc'\in {}^ZC={}^Z\mathsf {r}(C)$
, these are both units in
 $\widetilde {\mathcal {C}}(S)$
by what we just proved and hence
$\widetilde {\mathcal {C}}(S)$
by what we just proved and hence
This shows that every
 $[s,C]\in \widetilde {\mathcal {C}}(S)$
is invertible so
$[s,C]\in \widetilde {\mathcal {C}}(S)$
is invertible so
 $\widetilde {\mathcal {C}}(S)$
is a groupoid.
$\widetilde {\mathcal {C}}(S)$
is a groupoid.
Let
 $\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
denote the canonical projection onto
$\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
denote the canonical projection onto
![]() $\mathcal {C}(S)$
, that is,
$\mathcal {C}(S)$
, that is,
The canonical topology on
 $\widetilde {\mathcal {C}}(S)$
is generated by the sets
$\widetilde {\mathcal {C}}(S)$
is generated by the sets
 $$ \begin{align*} \widetilde{\mathcal{C}}^s&=\{[s,C]:s\in C\in\mathcal{C}(S)\},\\ \widetilde{\mathcal{C}}_s&=\{[c,C]:c,s\in C\in\mathcal{C}(S)\}=\rho_{\mathcal{C}}^{-1}[\mathcal{C}_s]. \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{C}}^s&=\{[s,C]:s\in C\in\mathcal{C}(S)\},\\ \widetilde{\mathcal{C}}_s&=\{[c,C]:c,s\in C\in\mathcal{C}(S)\}=\rho_{\mathcal{C}}^{-1}[\mathcal{C}_s]. \end{align*} $$
Theorem 10.2.
 $\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
is an étale bundle.
$\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
is an étale bundle.
Proof. To see that the inverse map on
 $\widetilde {\mathcal {C}}(S)$
is continuous, suppose that
$\widetilde {\mathcal {C}}(S)$
is continuous, suppose that
![]() $[a,A]^{-1}\in \widetilde {\mathcal {C}}^{b'}$
. This means that
$[a,A]^{-1}\in \widetilde {\mathcal {C}}^{b'}$
. This means that
![]() $[a,A]^{-1}=[b',A^*]$
so, in particular,
$[a,A]^{-1}=[b',A^*]$
so, in particular,
![]() $b'\in A^*$
. Taking
$b'\in A^*$
. Taking
![]() $b,c\in S$
with
$b,c\in S$
with
![]() $A\ni c<_{b'}b$
, (10-1) yields
$A\ni c<_{b'}b$
, (10-1) yields
![]() $[a,A]=[b',A^*]^{-1}=[b,A]$
, so
$[a,A]=[b',A^*]^{-1}=[b,A]$
, so
 $[a,A]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_c$
. Moreover, for any other
$[a,A]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_c$
. Moreover, for any other
 $[b,B]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_c$
, we see that
$[b,B]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_c$
, we see that
![]() $B\ni c<_{b'}b$
and hence
$B\ni c<_{b'}b$
and hence
![]() $[b,B]^{-1}=[b',B^*]\in \widetilde {\mathcal {C}}^{b'}$
, by (10-1). Likewise, as in the proof of Theorem 8.4, if
$[b,B]^{-1}=[b',B^*]\in \widetilde {\mathcal {C}}^{b'}$
, by (10-1). Likewise, as in the proof of Theorem 8.4, if
 $[a,A]^{-1}\in \widetilde {\mathcal {C}}_{b'}$
then again
$[a,A]^{-1}\in \widetilde {\mathcal {C}}_{b'}$
then again
![]() $b'\in A^*$
so, taking
$b'\in A^*$
so, taking
![]() $b,c\in S$
with
$b,c\in S$
with
![]() $A\ni c<_{b'}b$
, we see that
$A\ni c<_{b'}b$
, we see that
 $[a,A]\in \widetilde {\mathcal {C}}_c$
and
$[a,A]\in \widetilde {\mathcal {C}}_c$
and
 $(\widetilde {\mathcal {C}}_c)^{-1}\subseteq \widetilde {\mathcal {C}}_{b'}$
. Thus, the inverse map is continuous.
$(\widetilde {\mathcal {C}}_c)^{-1}\subseteq \widetilde {\mathcal {C}}_{b'}$
. Thus, the inverse map is continuous.
For the product, suppose that
![]() $[a,A][b,B]\in \widetilde {\mathcal {C}}^s$
. As
$[a,A][b,B]\in \widetilde {\mathcal {C}}^s$
. As
![]() $[a,A][b,B]=[ab,AB]$
, this means that
$[a,A][b,B]=[ab,AB]$
, this means that
![]() $ab\sim _{AB}s$
, so (9-6) yields
$ab\sim _{AB}s$
, so (9-6) yields
![]() $a'\in A^*$
and
$a'\in A^*$
and
![]() $b'\in B^*$
with
$b'\in B^*$
with
![]() $abb'a'=sb'a'$
. Taking
$abb'a'=sb'a'$
. Taking
![]() $a'',b'',c,d\in S$
with
$a'',b'',c,d\in S$
with
![]() $A\ni c<_{a'}a''$
and
$A\ni c<_{a'}a''$
and
![]() $B\ni d<_{b'}b''$
, we see that
$B\ni d<_{b'}b''$
, we see that
 $[a,A]\in \widetilde {\mathcal {C}}^a\cap \widetilde {\mathcal {C}}_c$
and
$[a,A]\in \widetilde {\mathcal {C}}^a\cap \widetilde {\mathcal {C}}_c$
and
 $[b,B]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_d$
. Also, for any other
$[b,B]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_d$
. Also, for any other
 $[a,C]\in \widetilde {\mathcal {C}}^a\cap \widetilde {\mathcal {C}}_c$
and
$[a,C]\in \widetilde {\mathcal {C}}^a\cap \widetilde {\mathcal {C}}_c$
and
 $[b,D]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_d$
such that
$[b,D]\in \widetilde {\mathcal {C}}^b\cap \widetilde {\mathcal {C}}_d$
such that
![]() $[a,C][b,D]$
is defined, (9-6) again yields
$[a,C][b,D]$
is defined, (9-6) again yields
![]() $ab\sim _{CD}s$
, as
$ab\sim _{CD}s$
, as
![]() $c\in C$
and
$c\in C$
and
![]() $d\in D$
, so
$d\in D$
, so
![]() $a'\in C^*$
and
$a'\in C^*$
and
![]() $b'\in D^*$
, and hence
$b'\in D^*$
, and hence
![]() $[a,C][b,D]=[ab,CD]\in \widetilde {\mathcal {C}}^s$
. Similarly, if
$[a,C][b,D]=[ab,CD]\in \widetilde {\mathcal {C}}^s$
. Similarly, if
 $[a,A][b,B]\in \widetilde {\mathcal {C}}_s$
, then we have
$[a,A][b,B]\in \widetilde {\mathcal {C}}_s$
, then we have
![]() $c\in A$
and
$c\in A$
and
![]() $d\in B$
with
$d\in B$
with
![]() $cd<s$
. Then
$cd<s$
. Then
 $[a,A]\in \widetilde {\mathcal {C}}_c$
and
$[a,A]\in \widetilde {\mathcal {C}}_c$
and
 $[b,B]\in \widetilde {\mathcal {C}}_d$
. Moreover, for any other
$[b,B]\in \widetilde {\mathcal {C}}_d$
. Moreover, for any other
 $[e,C]\in \widetilde {\mathcal {C}}_c$
and
$[e,C]\in \widetilde {\mathcal {C}}_c$
and
 $[f,D]\in \widetilde {\mathcal {C}}_d$
such that
$[f,D]\in \widetilde {\mathcal {C}}_d$
such that
![]() $[e,C][f,D]$
is defined,
$[e,C][f,D]$
is defined,
 $[e,C][f,D]=[ef,CD]\in \widetilde {\mathcal {C}}_{cd}\subseteq \widetilde {\mathcal {C}}_s$
. This shows that the product is continuous.
$[e,C][f,D]=[ef,CD]\in \widetilde {\mathcal {C}}_{cd}\subseteq \widetilde {\mathcal {C}}_s$
. This shows that the product is continuous.
So
 $\widetilde {\mathcal {C}}(S)$
is a topological groupoid, and we already know that
$\widetilde {\mathcal {C}}(S)$
is a topological groupoid, and we already know that
![]() $\mathcal {C}(S)$
is an étale groupoid, by Theorem 8.4. It only remains to prove that
$\mathcal {C}(S)$
is an étale groupoid, by Theorem 8.4. It only remains to prove that
![]() $\rho _{\mathcal {C}}$
is a locally injective continuous open isocofibration. Local injectivity is immediate from the fact that
$\rho _{\mathcal {C}}$
is a locally injective continuous open isocofibration. Local injectivity is immediate from the fact that
![]() $\rho _{\mathcal {C}}$
is injective on
$\rho _{\mathcal {C}}$
is injective on
![]() $\widetilde {\mathcal {C}}^s$
, for all
$\widetilde {\mathcal {C}}^s$
, for all
![]() $s\in S$
. Continuity is immediate from the fact that
$s\in S$
. Continuity is immediate from the fact that
 $\widetilde {\mathcal {C}}_s=\rho _{\mathcal {C}}^{-1}[\mathcal {C}_s]$
is open, for all
$\widetilde {\mathcal {C}}_s=\rho _{\mathcal {C}}^{-1}[\mathcal {C}_s]$
is open, for all
![]() $s\in S$
. The definition of the product on
$s\in S$
. The definition of the product on
![]() $\mathcal {C}(S)$
also immediately shows that
$\mathcal {C}(S)$
also immediately shows that
![]() $\rho _{\mathcal {C}}$
is an isocofibration.
$\rho _{\mathcal {C}}$
is an isocofibration.
To see that
![]() $\rho _{\mathcal {C}}$
is also open, suppose that F and G and finite subsets of S and
$\rho _{\mathcal {C}}$
is also open, suppose that F and G and finite subsets of S and
 $$ \begin{align*} [a,A]\in\widetilde{\mathcal{C}}^F_G=\bigcap_{f\in F}\widetilde{\mathcal{C}}^f\cap\bigcap_{g\in G}\widetilde{\mathcal{C}}_g. \end{align*} $$
$$ \begin{align*} [a,A]\in\widetilde{\mathcal{C}}^F_G=\bigcap_{f\in F}\widetilde{\mathcal{C}}^f\cap\bigcap_{g\in G}\widetilde{\mathcal{C}}_g. \end{align*} $$
For all
![]() $f\in F$
, this means that
$f\in F$
, this means that
![]() $a\sim _Af$
, so we have
$a\sim _Af$
, so we have
 $a^{\prime }_f\in A^*$
with
$a^{\prime }_f\in A^*$
with
 $aa^{\prime }_f=fa^{\prime }_f$
. Then we can take
$aa^{\prime }_f=fa^{\prime }_f$
. Then we can take
![]() $a_f,b_f\in S$
with
$a_f,b_f\in S$
with
 $A\ni b_f<_{a^{\prime }_f}a_f$
. Note that
$A\ni b_f<_{a^{\prime }_f}a_f$
. Note that
and hence
![]() $\rho _{\mathcal {C}}([a,A])=A\in \mathcal {C}_H$
. Moreover, for all
$\rho _{\mathcal {C}}([a,A])=A\in \mathcal {C}_H$
. Moreover, for all
![]() $B\in \mathcal {C}_H$
and
$B\in \mathcal {C}_H$
and
![]() $f\in F$
, note that
$f\in F$
, note that
![]() $b_f\in B$
, so
$b_f\in B$
, so
 $a^{\prime }_f\in B^*$
and hence
$a^{\prime }_f\in B^*$
and hence
![]() $a\sim _Bf$
. Thus,
$a\sim _Bf$
. Thus,
 $[a,B]\in \widetilde {\mathcal {C}}^F_G$
, so
$[a,B]\in \widetilde {\mathcal {C}}^F_G$
, so
 $B=\rho _{\mathcal {C}}([a,B])\in \rho _{\mathcal {C}}[\widetilde {\mathcal {C}}^F_G]$
, showing that
$B=\rho _{\mathcal {C}}([a,B])\in \rho _{\mathcal {C}}[\widetilde {\mathcal {C}}^F_G]$
, showing that
 $\mathcal {C}_H\subseteq \rho _{\mathcal {C}}[\widetilde {\mathcal {C}}^F_G]$
. This shows that
$\mathcal {C}_H\subseteq \rho _{\mathcal {C}}[\widetilde {\mathcal {C}}^F_G]$
. This shows that
![]() $\rho _{\mathcal {C}}$
is also an open map.
$\rho _{\mathcal {C}}$
is also an open map.
We refer to
 $\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
as the coset bundle.
$\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
as the coset bundle.
11 Representations
Recall the notion of an étale representation from Definition 8.9.
Definition 11.1. A bundle representation of the structured semigroup
![]() $(S,N,Z)$
on a groupoid bundle
$(S,N,Z)$
on a groupoid bundle
![]() $\pi :F\rightarrow G$
is a semigroup homomorphism
$\pi :F\rightarrow G$
is a semigroup homomorphism
![]() $\theta :S\rightarrow \mathcal {S}(\pi )$
such that
$\theta :S\rightarrow \mathcal {S}(\pi )$
such that
![]() $a\mapsto \mathrm {dom}(\theta (a))$
is an étale representation.
$a\mapsto \mathrm {dom}(\theta (a))$
is an étale representation.
If
![]() $\theta :S\rightarrow \mathcal {S}(\pi )$
is a semigroup homomorphism then so is
$\theta :S\rightarrow \mathcal {S}(\pi )$
is a semigroup homomorphism then so is
![]() $a\mapsto \mathrm {dom}(\theta (a))$
. To verify that it is an étale representation, it thus suffices to check that these domains cover G, (Locally Round) holds and N gets mapped to
$a\mapsto \mathrm {dom}(\theta (a))$
. To verify that it is an étale representation, it thus suffices to check that these domains cover G, (Locally Round) holds and N gets mapped to
![]() $\mathcal {O}(G^0)$
, that is,
$\mathcal {O}(G^0)$
, that is,
![]() $\theta [N]\subseteq \mathcal {N}(\pi )$
. Note that (Locally Round) here ensures that
$\theta [N]\subseteq \mathcal {N}(\pi )$
. Note that (Locally Round) here ensures that
![]() $\theta [S]$
is a local-inverse semigroup, as per Definition 3.8; see Proposition 5.2.
$\theta [S]$
is a local-inverse semigroup, as per Definition 3.8; see Proposition 5.2.
Again, we call a bundle representation
![]() $\mu :S\rightarrow \mathcal {S}(\pi )$
universal if, for every bundle representation
$\mu :S\rightarrow \mathcal {S}(\pi )$
universal if, for every bundle representation
![]() $\theta :S\rightarrow \mathcal {S}(\pi ')$
, there exists a unique Pierce morphism
$\theta :S\rightarrow \mathcal {S}(\pi ')$
, there exists a unique Pierce morphism
![]() $(\phi ,\tau )$
from
$(\phi ,\tau )$
from
![]() $\pi $
to
$\pi $
to
![]() $\pi '$
such that
$\pi '$
such that
![]() $\theta =({\tau }/{\phi })\circ \mu $
for
$\theta =({\tau }/{\phi })\circ \mu $
for
![]() ${\tau }/{\phi }:\mathcal {S}(\pi )\rightarrow \mathcal {S}(\pi ')$
defined as in Theorem 4.10.
${\tau }/{\phi }:\mathcal {S}(\pi )\rightarrow \mathcal {S}(\pi ')$
defined as in Theorem 4.10.
Theorem 11.2. If Z is symmetric then
![]() $a\mapsto \widetilde {a}$
is a universal bundle representation where
$a\mapsto \widetilde {a}$
is a universal bundle representation where
![]() $\widetilde {a}\in \mathcal {S}(\rho _{\mathcal {C}})$
is such that, for all
$\widetilde {a}\in \mathcal {S}(\rho _{\mathcal {C}})$
is such that, for all
![]() $C\in \mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
,
$C\in \mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
,
Proof. For any
![]() $a\in S$
,
$a\in S$
,
![]() $\mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
is a slice by Proposition 8.3. To see that
$\mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
is a slice by Proposition 8.3. To see that
![]() $\widetilde {a}$
is continuous, first note that
$\widetilde {a}$
is continuous, first note that
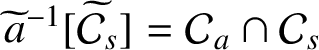 $\widetilde {a}^{-1}[\widetilde {\mathcal {C}}_s]=\mathcal {C}_a\cap \mathcal {C}_s$
. On the other hand, if
$\widetilde {a}^{-1}[\widetilde {\mathcal {C}}_s]=\mathcal {C}_a\cap \mathcal {C}_s$
. On the other hand, if
 $\widetilde {a}(C)=[a,C]\in \widetilde {\mathcal {C}}^s$
then
$\widetilde {a}(C)=[a,C]\in \widetilde {\mathcal {C}}^s$
then
![]() $az=sz$
, for some
$az=sz$
, for some
![]() $z\in C^Z$
. Take any
$z\in C^Z$
. Take any
![]() $b\in C$
with
$b\in C$
with
![]() $bz=b$
. If
$bz=b$
. If
![]() $B\in \mathcal {C}_a\cap \mathcal {C}_b$
then
$B\in \mathcal {C}_a\cap \mathcal {C}_b$
then
![]() $z\in B^Z$
and hence
$z\in B^Z$
and hence
 $\widetilde {a}(B)=[a,B]=[s,B]\in \widetilde {\mathcal {C}}^s$
. Thus,
$\widetilde {a}(B)=[a,B]=[s,B]\in \widetilde {\mathcal {C}}^s$
. Thus,
 $C\in \mathcal {C}_a\cap \mathcal {C}_b\subseteq \widetilde {a}^{-1}[\widetilde {\mathcal {C}}^s]$
. We have shown that preimages of subbasic sets are open and hence
$C\in \mathcal {C}_a\cap \mathcal {C}_b\subseteq \widetilde {a}^{-1}[\widetilde {\mathcal {C}}^s]$
. We have shown that preimages of subbasic sets are open and hence
![]() $\widetilde {a}$
is continuous.
$\widetilde {a}$
is continuous.
If Z is symmetric then
![]() $a\mapsto \mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
is an étale representation, thanks to Theorem 8.11. In particular, for any
$a\mapsto \mathrm {dom}(\widetilde {a})=\mathcal {C}_a$
is an étale representation, thanks to Theorem 8.11. In particular, for any
![]() $a,b\in S$
,
$a,b\in S$
,
 $\mathrm {dom}(\widetilde {\,ab\,})=\mathrm {dom}(\widetilde {a})\cdot \mathrm {dom}(\widetilde {b})$
and, for any
$\mathrm {dom}(\widetilde {\,ab\,})=\mathrm {dom}(\widetilde {a})\cdot \mathrm {dom}(\widetilde {b})$
and, for any
![]() $A\in \mathrm {dom}(\kern1pt\widetilde {a})$
and
$A\in \mathrm {dom}(\kern1pt\widetilde {a})$
and
 $B\in \mathrm {dom}(\widetilde {b})$
with
$B\in \mathrm {dom}(\widetilde {b})$
with
![]() $\mathsf {s}(A)=\mathsf {r}(B)$
,
$\mathsf {s}(A)=\mathsf {r}(B)$
,
 $$ \begin{align*} \widetilde{\,ab\,}(A\cdot B)=[ab,AB]=[a,A][b,B]=\widetilde{a}(A)\widetilde{b}(B). \end{align*} $$
$$ \begin{align*} \widetilde{\,ab\,}(A\cdot B)=[ab,AB]=[a,A][b,B]=\widetilde{a}(A)\widetilde{b}(B). \end{align*} $$
This shows that
![]() $\widetilde {\,ab\,}=\widetilde {a}\widetilde {b}$
, which in turn shows that
$\widetilde {\,ab\,}=\widetilde {a}\widetilde {b}$
, which in turn shows that
![]() $a\mapsto \widetilde {a}$
is a semigroup homomorphism and hence a bundle representation.
$a\mapsto \widetilde {a}$
is a semigroup homomorphism and hence a bundle representation.
To see that
![]() $a\mapsto \widetilde {a}$
is universal, take a bundle representation
$a\mapsto \widetilde {a}$
is universal, take a bundle representation
![]() $\theta :S\rightarrow \mathcal {S}(\pi )$
. By Theorem 8.11, we have a unique étale morphism
$\theta :S\rightarrow \mathcal {S}(\pi )$
. By Theorem 8.11, we have a unique étale morphism
![]() $\phi :G\rightarrow \mathcal {C}(S)$
such that
$\phi :G\rightarrow \mathcal {C}(S)$
such that
![]() $\mathrm {dom}(\theta (a))=\phi ^{-1}[\mathcal {C}_a]$
, for all
$\mathrm {dom}(\theta (a))=\phi ^{-1}[\mathcal {C}_a]$
, for all
![]() $a\in S$
. Indeed, the proof shows, for all
$a\in S$
. Indeed, the proof shows, for all
![]() $g\in G$
, that
$g\in G$
, that
We claim we have a continuous functor
 $\tau :\phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)\rightarrow F$
given by
$\tau :\phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)\rightarrow F$
given by
To see that
![]() $\tau $
is well defined, take
$\tau $
is well defined, take
![]() $a,b\in \phi (g)$
with
$a,b\in \phi (g)$
with
![]() $a\sim _{\phi (g)}b$
. Then
$a\sim _{\phi (g)}b$
. Then
![]() $as=bs$
, for some
$as=bs$
, for some
![]() $s\in \phi (g)^*=\phi (g^{-1})$
, and hence
$s\in \phi (g)^*=\phi (g^{-1})$
, and hence
Multiplying by
![]() $\theta (s)(g^{-1})^{-1}$
yields
$\theta (s)(g^{-1})^{-1}$
yields
![]() $\theta (a)(g)=\theta (b)(g)$
, as required. To see that
$\theta (a)(g)=\theta (b)(g)$
, as required. To see that
![]() $\tau $
is a functor, note that
$\tau $
is a functor, note that
 $([a,\phi (g)],g),([b,\phi (h)],h)\in \phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)$
and
$([a,\phi (g)],g),([b,\phi (h)],h)\in \phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)$
and
![]() $\mathsf {s}(g)=\mathsf {r}(h)$
implies
$\mathsf {s}(g)=\mathsf {r}(h)$
implies
 $$ \begin{align*} \tau(([a,\phi(g)],g)([b,\phi(h)],h))&=\tau([ab,\phi(gh)],gh)=\theta(ab)(gh)=\theta(a)(g)\theta(b)(h)\\ &=\tau([a,\phi(g)],g)\tau([b,\phi(h)],h). \end{align*} $$
$$ \begin{align*} \tau(([a,\phi(g)],g)([b,\phi(h)],h))&=\tau([ab,\phi(gh)],gh)=\theta(ab)(gh)=\theta(a)(g)\theta(b)(h)\\ &=\tau([a,\phi(g)],g)\tau([b,\phi(h)],h). \end{align*} $$
For continuity, note that if
![]() $\tau ([a,\phi (g)],g)=\theta (a)(g)\in O$
, for some open
$\tau ([a,\phi (g)],g)=\theta (a)(g)\in O$
, for some open
![]() $O\subseteq F$
, then the continuity of
$O\subseteq F$
, then the continuity of
![]() $\theta (a)$
yields open
$\theta (a)$
yields open
![]() $O'\subseteq G$
with
$O'\subseteq G$
with
![]() $g\in O'$
and
$g\in O'$
and
![]() $\theta (a)[O']\subseteq O$
. Then
$\theta (a)[O']\subseteq O$
. Then
 $([a,\phi (g)],g)\in \widetilde {C}^a\times O'$
and, for any other
$([a,\phi (g)],g)\in \widetilde {C}^a\times O'$
and, for any other
 $([a,\phi (h)],h)\in (\widetilde {C}^a\times O')$
, we see that
$([a,\phi (h)],h)\in (\widetilde {C}^a\times O')$
, we see that
This shows that
![]() $\tau $
is continuous, completing the proof of the claim. Furthermore, noting that
$\tau $
is continuous, completing the proof of the claim. Furthermore, noting that
![]() $\pi (\tau ([a,\phi (g)],g))=\pi (\theta (a)(g))=g=\rho _{\mathcal {C}\phi }([a,\phi (g)],g)$
, that is,
$\pi (\tau ([a,\phi (g)],g))=\pi (\theta (a)(g))=g=\rho _{\mathcal {C}\phi }([a,\phi (g)],g)$
, that is,
![]() $\pi \circ \tau =\rho _{\mathcal {C}\phi }$
, we see that
$\pi \circ \tau =\rho _{\mathcal {C}\phi }$
, we see that
![]() $(\phi ,\tau )$
is a Pierce morphism from
$(\phi ,\tau )$
is a Pierce morphism from
![]() $\rho _{\mathcal {C}}$
to
$\rho _{\mathcal {C}}$
to
![]() $\pi $
.
$\pi $
.
For all
![]() $g\in G$
and
$g\in G$
and
![]() $a\in \phi (g)$
, we see that
$a\in \phi (g)$
, we see that
 $$ \begin{align*} \theta(a)(g)=\tau([a,\phi(g)],g)=\tau(\widetilde{a}(\phi(g)),g)=\tau((\widetilde{a}\circ\phi)(g),g)=\frac{\tau}{\phi}(\widetilde{a})(g), \end{align*} $$
$$ \begin{align*} \theta(a)(g)=\tau([a,\phi(g)],g)=\tau(\widetilde{a}(\phi(g)),g)=\tau((\widetilde{a}\circ\phi)(g),g)=\frac{\tau}{\phi}(\widetilde{a})(g), \end{align*} $$
where
![]() ${\tau }/{\phi }:\mathcal {S}(\rho _{\mathcal {C}})\rightarrow \mathcal {S}(\pi )$
is the homomorphism from Theorem 4.10. Also
${\tau }/{\phi }:\mathcal {S}(\rho _{\mathcal {C}})\rightarrow \mathcal {S}(\pi )$
is the homomorphism from Theorem 4.10. Also
 $$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(\widetilde{a})\bigg)=\phi^{-1}[\mathrm{dom}(\widetilde{a})]=\phi^{-1}[\mathcal{C}_a]=\mathrm{dom}(\theta(a)) \end{align*} $$
$$ \begin{align*} \mathrm{dom}\bigg(\frac{\tau}{\phi}(\widetilde{a})\bigg)=\phi^{-1}[\mathrm{dom}(\widetilde{a})]=\phi^{-1}[\mathcal{C}_a]=\mathrm{dom}(\theta(a)) \end{align*} $$
and hence
![]() $\theta (a)=({\tau }/{\phi })(\widetilde {a})$
, for all
$\theta (a)=({\tau }/{\phi })(\widetilde {a})$
, for all
![]() $a\in S$
, that is,
$a\in S$
, that is,
 $\theta =({\tau }/{\phi })\circ \widetilde {\mathcal {C}}$
, where
$\theta =({\tau }/{\phi })\circ \widetilde {\mathcal {C}}$
, where
 $\widetilde {\mathcal {C}}(a)=\widetilde {a}$
.
$\widetilde {\mathcal {C}}(a)=\widetilde {a}$
.
To see that
![]() $(\phi ,\tau )$
is unique, take another Pierce morphism
$(\phi ,\tau )$
is unique, take another Pierce morphism
![]() $(\phi ',\tau ')$
such that
$(\phi ',\tau ')$
such that
 ${\theta =({\tau '}/{\phi '})\circ \widetilde {\mathcal {C}}}$
. It follows that
${\theta =({\tau '}/{\phi '})\circ \widetilde {\mathcal {C}}}$
. It follows that
![]() $a\mapsto \mathrm {dom}(\theta (a))=\mathrm {dom}(({\tau '}/{\phi '})(\widetilde {a}))=\phi ^{\prime -1}[\mathcal {C}_a]$
is an étale morphism and hence
$a\mapsto \mathrm {dom}(\theta (a))=\mathrm {dom}(({\tau '}/{\phi '})(\widetilde {a}))=\phi ^{\prime -1}[\mathcal {C}_a]$
is an étale morphism and hence
![]() $\phi '=\phi $
, by the uniqueness part of Theorem 8.11. Now, for any
$\phi '=\phi $
, by the uniqueness part of Theorem 8.11. Now, for any
 $([a,\phi (g)],g)\in \phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)$
, just note that
$([a,\phi (g)],g)\in \phi ^{\rho _{\mathcal {C}}}\widetilde {\mathcal {C}}(S)$
, just note that
 $$ \begin{align*} \tau'([a,\phi(g)],g)=\frac{\tau'}{\phi'}(\widetilde{a})(g)=\theta(a)(g)=\tau([a,\phi(g)],g). \end{align*} $$
$$ \begin{align*} \tau'([a,\phi(g)],g)=\frac{\tau'}{\phi'}(\widetilde{a})(g)=\theta(a)(g)=\tau([a,\phi(g)],g). \end{align*} $$
Thus,
![]() $\tau '=\tau $
, proving uniqueness and hence universality.
$\tau '=\tau $
, proving uniqueness and hence universality.
It follows that cosets and their equivalence classes determine when structured semigroups have faithful bundle representations, at least under symmetry.
Corollary 11.3. If Z is symmetric then the following assertions are equivalent.
(1)
 $(S,N,Z)$
has a faithful bundle representation.
$(S,N,Z)$
has a faithful bundle representation.(2) The coset bundle representation of
 $(S,N,Z)$
is faithful.
$(S,N,Z)$
is faithful.(3) For all distinct
 $a,b\in S$
, we have
$a,b\in S$
, we have
 $C\in {\mathcal {C}}(S)$
with
$C\in {\mathcal {C}}(S)$
with
 $\{a,b\}\cap C\neq \emptyset $
and
$\{a,b\}\cap C\neq \emptyset $
and  $$ \begin{align*} a\not\sim_C b. \end{align*} $$
$$ \begin{align*} a\not\sim_C b. \end{align*} $$
Proof. Certainly (2) implies (1). Conversely, if
![]() $\theta $
is a faithful bundle representation then Theorem 11.2 yields a Pierce morphism
$\theta $
is a faithful bundle representation then Theorem 11.2 yields a Pierce morphism
![]() $(\phi ,\tau )$
such that
$(\phi ,\tau )$
such that
 $\theta =({\tau }/{\phi })\circ \widetilde {\mathcal {C}}$
, where
$\theta =({\tau }/{\phi })\circ \widetilde {\mathcal {C}}$
, where
![]() $\widetilde {\mathcal {C}}$
is the coset bundle representation. As
$\widetilde {\mathcal {C}}$
is the coset bundle representation. As
![]() $\theta $
is injective, so is
$\theta $
is injective, so is
![]() $\widetilde {\mathcal {C}}$
, showing that (1) implies (2).
$\widetilde {\mathcal {C}}$
, showing that (1) implies (2).
More explicitly, (2) is saying that, for any distinct
![]() $a,b\in S$
, we have
$a,b\in S$
, we have
![]() $C\in \mathcal {C}(S)$
such that either only one of
$C\in \mathcal {C}(S)$
such that either only one of
![]() $\widetilde {a}$
and
$\widetilde {a}$
and
![]() $\widetilde {b}$
is defined at C, so certainly
$\widetilde {b}$
is defined at C, so certainly
![]() $a \not \sim _C b$
, or they are both defined at C but have different values at C, that is,
$a \not \sim _C b$
, or they are both defined at C but have different values at C, that is,
 $$ \begin{align*} [a,C]=\widetilde{a}(C)\neq\widetilde{b}(C)=[b,C], \end{align*} $$
$$ \begin{align*} [a,C]=\widetilde{a}(C)\neq\widetilde{b}(C)=[b,C], \end{align*} $$
which again means
![]() $a\not \sim _Cb$
. We immediately see this is equivalent to (3).
$a\not \sim _Cb$
. We immediately see this is equivalent to (3).
Unlike the situation with inverse semigroups in Proposition 2.4, it is indeed possible for a (symmetric) structured semigroup to have no faithful representations.
Example 11.4. Take
![]() $S=N=Z=\{0,a\}$
where
$S=N=Z=\{0,a\}$
where
![]() $a^2=a0=0a=00=0$
. This is certainly a structured semigroup with symmetric Z. For any representation
$a^2=a0=0a=00=0$
. This is certainly a structured semigroup with symmetric Z. For any representation
![]() $a\mapsto \widehat {a}$
on a groupoid bundle
$a\mapsto \widehat {a}$
on a groupoid bundle
![]() $\pi :F\rightarrow G$
, we would have
$\pi :F\rightarrow G$
, we would have
 $\mathrm {dom}(\widehat {a})=\mathrm {dom}(\widehat {0})\subseteq G^0$
, as
$\mathrm {dom}(\widehat {a})=\mathrm {dom}(\widehat {0})\subseteq G^0$
, as
![]() $a^2=0\in N$
, and
$a^2=0\in N$
, and
 $\mathrm {ran}(\widehat {0})\subseteq F^0$
, as
$\mathrm {ran}(\widehat {0})\subseteq F^0$
, as
![]() $00=0$
, and hence
$00=0$
, and hence
![]() $\widehat {0}=\widehat {a0}=\widehat {a}\widehat {0}=\widehat {a}$
, showing that the representation cannot be faithful.
$\widehat {0}=\widehat {a0}=\widehat {a}\widehat {0}=\widehat {a}$
, showing that the representation cannot be faithful.
Remark 11.5. On the one hand, this might motivate one to look for even more general kinds of representations than those arising from slice-sections of groupoid bundles. On the other hand, one might look for some natural restrictions or additional structures to place on structured semigroups to ensure that they do have faithful bundle representations. In our subsequent work (see [Reference Bice2, Reference Bice3]) we actually do a bit of both, considering semigroups that sit nicely within larger rings and their representations as sections of more general category bundles.
12 Filters
As usual, we call
![]() $D\subseteq S$
directed if
$D\subseteq S$
directed if
A filter is a directed up-set
![]() $D=D^<$
. So the nonempty directed cosets
$D=D^<$
. So the nonempty directed cosets
are all filters. Directed cosets offer a number of advantages over arbitrary cosets. For example, one immediately notes that the canonical subbasis of
![]() $\mathcal {C}(S)$
becomes a basis when restricted to
$\mathcal {C}(S)$
becomes a basis when restricted to
![]() $\mathcal {D}(S)$
, namely
$\mathcal {D}(S)$
, namely
![]() $(\mathcal {D}_a)_{a\in S}$
, where
$(\mathcal {D}_a)_{a\in S}$
, where
![]() $\mathcal {D}_a=\mathcal {C}_a\cap \mathcal {D}(S)$
. Our goal here is to show that the directed coset subbundle is still a groupoid bundle and that the corresponding subrepresentation of S is ‘Zakrzewski universal’.
$\mathcal {D}_a=\mathcal {C}_a\cap \mathcal {D}(S)$
. Our goal here is to show that the directed coset subbundle is still a groupoid bundle and that the corresponding subrepresentation of S is ‘Zakrzewski universal’.
Remark 12.1. There will be plenty of directed cosets arising from principal filters in our primary motivating examples, as already noted in Remark 7.2. But in general, a structured semigroup S may have few directed cosets; again we see in Corollary 12.19 below that we have faithful bundle representations precisely when there are enough directed cosets to distinguish the elements of S via their corresponding equivalence relations, at least when Z is symmetric.
First we look at products. Recall the notation
![]() $c\mid D$
from Definition 7.5.
$c\mid D$
from Definition 7.5.
Proposition 12.2. For any
![]() $c\in S$
and
$c\in S$
and
![]() $D\subseteq S$
,
$D\subseteq S$
,
Proof. If
![]() $c'cd=d\in D$
and D is directed then, for any
$c'cd=d\in D$
and D is directed then, for any
![]() $a,b\in D$
, we have
$a,b\in D$
, we have
![]() $e\in D$
with
$e\in D$
with
![]() $e<a,b,d$
. In particular, we have
$e<a,b,d$
. In particular, we have
![]() $d'\in S$
with
$d'\in S$
with
![]() $e<_{d'}d$
and hence
$e<_{d'}d$
and hence
![]() $e=dd'e=c'cdd'e=c'ce$
. Then (
Z-Splitting) (applied to
$e=dd'e=c'cdd'e=c'ce$
. Then (
Z-Splitting) (applied to
![]() $S^{\mathrm {op}}$
) yields
$S^{\mathrm {op}}$
) yields
![]() $ce<ca,cb$
, showing that
$ce<ca,cb$
, showing that
![]() $cD$
is directed.
$cD$
is directed.
Likewise, duals respect directedness.
Proposition 12.3. If
![]() $D\subseteq S$
is directed then so is
$D\subseteq S$
is directed then so is
![]() $D^*$
and
$D^*$
and
Proof. Take
![]() $b',d'\in D^*$
, so we have
$b',d'\in D^*$
, so we have
![]() $a,b,c,d\in S$
with
$a,b,c,d\in S$
with
![]() $D\ni a<_{b'}b$
and
$D\ni a<_{b'}b$
and
![]() $D\ni c<_{d'}d$
. As D is directed, we have
$D\ni c<_{d'}d$
. As D is directed, we have
![]() $e,f\in D$
with
$e,f\in D$
with
![]() $e<_{f'}f< a,c$
so (Transitivity) yields
$e<_{f'}f< a,c$
so (Transitivity) yields
![]() $e,f<_{b'}b$
and
$e,f<_{b'}b$
and
![]() $e,f<_{d'}d$
. Then (Switch) yields
$e,f<_{d'}d$
. Then (Switch) yields
![]() $b'fd'<_bb'$
and
$b'fd'<_bb'$
and
![]() $b'fd'<_dd'$
. Also
$b'fd'<_dd'$
. Also
![]() $e<_{b'fd'}df'b$
, as
$e<_{b'fd'}df'b$
, as
![]() $eb'fd'\in NN\subseteq N$
and
$eb'fd'\in NN\subseteq N$
and
![]() $eb'fd'df'b=eb'ff'b=ff'eb'b=e$
. Thus,
$eb'fd'df'b=eb'ff'b=ff'eb'b=e$
. Thus,
![]() $b'fd'\in D^*$
, showing that
$b'fd'\in D^*$
, showing that
![]() $D^*$
is indeed directed.
$D^*$
is indeed directed.
Now suppose that
![]() $e\in D$
and
$e\in D$
and
![]() $b',d'\in D^*$
, so we again have
$b',d'\in D^*$
, so we again have
![]() $a,b,c,d\in S$
with
$a,b,c,d\in S$
with
![]() $D\ni a<_{b'}b$
and
$D\ni a<_{b'}b$
and
![]() $D\ni c<_{d'}d$
. As D is directed, we have
$D\ni c<_{d'}d$
. As D is directed, we have
![]() $f,g\in D$
with
$f,g\in D$
with
![]() $g<_{f'}f<a,c,e$
. We immediately verify that
$g<_{f'}f<a,c,e$
. We immediately verify that
![]() $g<_{b'fd'}df'b$
(for example,
$g<_{b'fd'}df'b$
(for example,
![]() $gb'fd'df'b=gd'db'ff'b=ff'gb'b=g$
) so
$gb'fd'df'b=gd'db'ff'b=ff'gb'b=g$
) so
![]() $b'fd'\in D^*$
. Taking
$b'fd'\in D^*$
. Taking
![]() $e'\in S$
with
$e'\in S$
with
![]() $f<_{e'}e$
, we also immediately verify that
$f<_{e'}e$
, we also immediately verify that
![]() $b'fd'<_{de'b}b'ed'$
(for example,
$b'fd'<_{de'b}b'ed'$
(for example,
![]() $b'fd'de'bb'ed'=b'fe'bb'ed'=b'bb'fe'ed'=b'fd'$
) and hence
$b'fd'de'bb'ed'=b'fe'bb'ed'=b'bb'fe'ed'=b'fd'$
) and hence
![]() $b'ed'\in D^{*<}$
, showing that
$b'ed'\in D^{*<}$
, showing that
![]() $D^*DD^*\subseteq D^{*<}$
.
$D^*DD^*\subseteq D^{*<}$
.
When N is diagonal, directed cosets are precisely filters and, moreover, for any
 $(d^{\sim _D},D)\in \widetilde {\mathcal {D}}(S)$
, the second coordinate is just the up-closure of the first (where
$(d^{\sim _D},D)\in \widetilde {\mathcal {D}}(S)$
, the second coordinate is just the up-closure of the first (where
 $\widetilde {\mathcal {D}}(S)=\rho _{\mathcal {C}}^{-1}[\mathcal {D}(S)]=\{(d^{\sim _D},D)\in \widetilde {\mathcal {C}}(S):D\in \mathcal {D}(S)\}$
).
$\widetilde {\mathcal {D}}(S)=\rho _{\mathcal {C}}^{-1}[\mathcal {D}(S)]=\{(d^{\sim _D},D)\in \widetilde {\mathcal {C}}(S):D\in \mathcal {D}(S)\}$
).
Proposition 12.4. Any directed
![]() $D=D^{**}\subseteq S$
is a filter and a coset. Conversely, if N is diagonal then every filter is a coset and
$D=D^{**}\subseteq S$
is a filter and a coset. Conversely, if N is diagonal then every filter is a coset and
Proof. As D is directed and hence round,
![]() $D^<\subseteq D^{<<}\subseteq D^{**}=D$
, that is, D is also an up-set and hence a filter. Also (Antimorphism), (6-1) and (12-2) yield
$D^<\subseteq D^{<<}\subseteq D^{**}=D$
, that is, D is also an up-set and hence a filter. Also (Antimorphism), (6-1) and (12-2) yield
so D is also a coset.
When N is diagonal, any filter
![]() $D\subseteq S$
satisfies
$D\subseteq S$
satisfies
![]() $D=D^{<<}=D^{**}$
by (6-5), and is thus a coset by the above argument. Moreover, for any
$D=D^{<<}=D^{**}$
by (6-5), and is thus a coset by the above argument. Moreover, for any
![]() $c,d\in D$
, we have
$c,d\in D$
, we have
![]() $a,b',b\in S$
with
$a,b',b\in S$
with
![]() $D\ni a<_{b'}b<c,d$
. Taking
$D\ni a<_{b'}b<c,d$
. Taking
![]() $c',d'\in D$
with
$c',d'\in D$
with
![]() $b<_{c'}c$
and
$b<_{c'}c$
and
![]() $b<_{d'}d$
, we see that
$b<_{d'}d$
, we see that
![]() $cc'bb'd=bb'd$
and
$cc'bb'd=bb'd$
and
![]() $c'bb'd=c'dd'bb'd\in N$
by diagonality, because
$c'bb'd=c'dd'bb'd\in N$
by diagonality, because
![]() $c'dd'b,d'b,d'bb'd\in N$
. Thus,
$c'dd'b,d'b,d'bb'd\in N$
. Thus,
![]() $d\sim _Dbb'd<_{c'}c$
, by (9-7), that is,
$d\sim _Dbb'd<_{c'}c$
, by (9-7), that is,
![]() $c\in (d^{\sim _D})^<$
, showing that
$c\in (d^{\sim _D})^<$
, showing that
![]() $D\subseteq (d^{\sim _D})^<\subseteq D^<\subseteq D$
.
$D\subseteq (d^{\sim _D})^<\subseteq D^<\subseteq D$
.
Definition 12.5. In a groupoid G, we call
![]() $I\subseteq G$
an ideal if
$I\subseteq G$
an ideal if
for all
![]() $(g,h)\in G^2$
.
$(g,h)\in G^2$
.
In particular, if
![]() $I\subseteq G$
is an ideal then
$I\subseteq G$
is an ideal then
![]() $g\in I$
implies
$g\in I$
implies
![]() $gg^{-1}\in I$
and hence
$gg^{-1}\in I$
and hence
![]() $g^{-1}=g^{-1}gg^{-1}\in I$
, that is,
$g^{-1}=g^{-1}gg^{-1}\in I$
, that is,
![]() $I=I^{-1}=II$
. It follows that ideals are precisely the replete/isomorphism-closed full subgroupoids. Moreover, if G has an étale topology, the subspace topology on any ideal is again étale; see [Reference Bice1]. In particular,
$I=I^{-1}=II$
. It follows that ideals are precisely the replete/isomorphism-closed full subgroupoids. Moreover, if G has an étale topology, the subspace topology on any ideal is again étale; see [Reference Bice1]. In particular,
![]() $\mathcal {D}(S)$
is an étale subgroupoid of
$\mathcal {D}(S)$
is an étale subgroupoid of
![]() $\mathcal {C}(S)$
, by the following result.
$\mathcal {C}(S)$
, by the following result.
Proposition 12.6.
![]() $\mathcal {D}(S)$
is an ideal of
$\mathcal {D}(S)$
is an ideal of
![]() $\mathcal {C}(S)$
(and hence an étale groupoid).
$\mathcal {C}(S)$
(and hence an étale groupoid).
Proof. If
![]() $C\in \mathcal {C}(S)$
,
$C\in \mathcal {C}(S)$
,
![]() $D\in \mathcal {D}(S)$
and
$D\in \mathcal {D}(S)$
and
![]() $(C,D)\in \mathcal {C}^2$
then
$(C,D)\in \mathcal {C}^2$
then
![]() $cD$
is directed, by (12-1), and hence so is
$cD$
is directed, by (12-1), and hence so is
![]() $(CD)^*=(cD)^*$
and
$(CD)^*=(cD)^*$
and
![]() $(CD)^{**}$
, by Proposition 12.2 and (7-2). Likewise,
$(CD)^{**}$
, by Proposition 12.2 and (7-2). Likewise,
![]() $(D,C)\in \mathcal {C}^2$
implies that
$(D,C)\in \mathcal {C}^2$
implies that
![]() $(DC)^{**}$
is directed and hence
$(DC)^{**}$
is directed and hence
![]() $\mathcal {D}(S)$
is an ideal.
$\mathcal {D}(S)$
is an ideal.
Next, we note that units in
![]() $\mathcal {D}(S)$
are just units in
$\mathcal {D}(S)$
are just units in
![]() $\mathcal {C}(S)$
generated by N.
$\mathcal {C}(S)$
generated by N.
Proposition 12.7. Let
![]() $U\in \mathcal {C}(S)$
be a unit coset.
$U\in \mathcal {C}(S)$
be a unit coset.
(1)
 $(U\cap N)^<$
is a directed unit coset.
$(U\cap N)^<$
is a directed unit coset.(2)
 $(U\cap N)^<=U$
when U is directed.
$(U\cap N)^<=U$
when U is directed.(3)
 $(U\cap N)^<=U^{Z<}$
when N is diagonal.
$(U\cap N)^<=U^{Z<}$
when N is diagonal.
Proof. (1) First we claim that
![]() $U\cap N$
is directed. Indeed, if
$U\cap N$
is directed. Indeed, if
![]() $m,n\in U\cap N$
then we have
$m,n\in U\cap N$
then we have
![]() $U\ni t<_{m'}m$
and
$U\ni t<_{m'}m$
and
![]() $U\ni u<_{n'}n$
. Noting that
$U\ni u<_{n'}n$
. Noting that
![]() $t=(tm')m\in NN\subseteq N$
and
$t=(tm')m\in NN\subseteq N$
and
![]() $u=(un')n\in NN\subseteq N$
, it follows that
$u=(un')n\in NN\subseteq N$
, it follows that
![]() $tu\in NN\subseteq N$
. As U is a unit coset,
$tu\in NN\subseteq N$
. As U is a unit coset,
![]() $tu\in UU=UU^*\subseteq U$
. Thus,
$tu\in UU=UU^*\subseteq U$
. Thus,
![]() $U\cap N\ni tu<m,n$
, by (
N-Invariance). This proves the claim, and hence
$U\cap N\ni tu<m,n$
, by (
N-Invariance). This proves the claim, and hence
![]() $(U\cap N)^<$
and
$(U\cap N)^<$
and
![]() $(U\cap N)^{<**}$
are also directed, by Proposition 12.2.
$(U\cap N)^{<**}$
are also directed, by Proposition 12.2.
Moreover, by Proposition 8.2,
Also, for any
![]() $u\in (U\cap N)^{<**}\subseteq U^{<**}=U$
and
$u\in (U\cap N)^{<**}\subseteq U^{<**}=U$
and
![]() $n\in U\cap N\subseteq (U\cap N)^{<**}$
, directedness yields
$n\in U\cap N\subseteq (U\cap N)^{<**}$
, directedness yields
![]() $t\in (U\cap N)^{<**}\subseteq U$
with
$t\in (U\cap N)^{<**}\subseteq U$
with
![]() $t<u,n$
. Then
$t<u,n$
. Then
![]() $t\in N$
too, as
$t\in N$
too, as
![]() $n\in N$
, that is,
$n\in N$
, that is,
![]() $t\in U\cap N$
and hence
$t\in U\cap N$
and hence
![]() $u\in (U\cap N)^<$
. This proves that
$u\in (U\cap N)^<$
. This proves that
![]() $(U\cap N)^<=(U\cap N)^{<**}$
and hence
$(U\cap N)^<=(U\cap N)^{<**}$
and hence
![]() $(U\cap N)^<$
is a unit coset, by Propositions 8.2 and 12.3.
$(U\cap N)^<$
is a unit coset, by Propositions 8.2 and 12.3.
(2) In particular, if
![]() $U=(U\cap N)^<$
then U is directed. Conversely, if U is directed then, as above, for any
$U=(U\cap N)^<$
then U is directed. Conversely, if U is directed then, as above, for any
![]() $u\in U$
and
$u\in U$
and
![]() $n\in U\cap N$
, we have
$n\in U\cap N$
, we have
![]() $t\in U$
with
$t\in U$
with
![]() $t<u,n$
and hence
$t<u,n$
and hence
![]() $t\in N$
, as
$t\in N$
, as
![]() $n\in N$
. Thus,
$n\in N$
. Thus,
![]() $u\in \!(U\cap N)^<$
, showing that
$u\in \!(U\cap N)^<$
, showing that
![]() $U\subseteq \!(U\cap N)^<\!\subseteq \! U^<=U$
.
$U\subseteq \!(U\cap N)^<\!\subseteq \! U^<=U$
.
(3) By (9-1),
![]() $U^Z\subseteq \mathsf {s}(U)\cap Z\subseteq U\cap N$
and hence
$U^Z\subseteq \mathsf {s}(U)\cap Z\subseteq U\cap N$
and hence
![]() $U^{Z<}\subseteq (U\cap N)^<$
. For the reverse inclusion, assume that N is diagonal and take
$U^{Z<}\subseteq (U\cap N)^<$
. For the reverse inclusion, assume that N is diagonal and take
![]() $u\in (U\cap N)^<$
so we have
$u\in (U\cap N)^<$
so we have
![]() $t,u'\in S$
with
$t,u'\in S$
with
![]() $U\cap N\ni t<_{u'}u$
. Then we can further take
$U\cap N\ni t<_{u'}u$
. Then we can further take
![]() $s,t'\in S$
with
$s,t'\in S$
with
![]() $U\ni s<_{t'}t$
. As
$U\ni s<_{t'}t$
. As
![]() $t't,t,tu'\in N$
and N is diagonal,
$t't,t,tu'\in N$
and N is diagonal,
![]() $t'tu'\in N$
and hence
$t'tu'\in N$
and hence
![]() $U^Z\ni t't<_{u'}u$
, showing that
$U^Z\ni t't<_{u'}u$
, showing that
![]() $(U\cap N)^<\subseteq U^{Z<}$
.
$(U\cap N)^<\subseteq U^{Z<}$
.
While
![]() $\mathcal {D}(S)$
might have a nice basis, it need not be Hausdorff or even
$\mathcal {D}(S)$
might have a nice basis, it need not be Hausdorff or even
![]() $T_1$
(when
$T_1$
(when
![]() $C\subsetneqq D$
, for
$C\subsetneqq D$
, for
![]() $C,D\in \mathcal {D}(S)$
, any neighbourhood of C is a neighbourhood of D). For better separation properties, we can consider ultrafilters
$C,D\in \mathcal {D}(S)$
, any neighbourhood of C is a neighbourhood of D). For better separation properties, we can consider ultrafilters
at least when Z has a zero, that is,
![]() $0s=s0=0\in Z$
, for all
$0s=s0=0\in Z$
, for all
![]() $s\in S$
.
$s\in S$
.
Theorem 12.8. If Z has a zero then
![]() $\mathcal {U}(S)$
is a locally Hausdorff ideal.
$\mathcal {U}(S)$
is a locally Hausdorff ideal.
Proof. First, note that
![]() $0<_0s$
, for all
$0<_0s$
, for all
![]() $s\in S$
, as
$s\in S$
, as
![]() $0\in Z\subseteq N$
. So a filter
$0\in Z\subseteq N$
. So a filter
![]() $F\subseteq S$
is proper precisely when
$F\subseteq S$
is proper precisely when
![]() $0\notin F$
.
$0\notin F$
.
Next, we show that every
![]() $U\in \mathcal {U}(S)$
is a coset. By (6-2),
$U\in \mathcal {U}(S)$
is a coset. By (6-2),
![]() $U=U^{<<}\subseteq U^{**}$
. As
$U=U^{<<}\subseteq U^{**}$
. As
![]() $0\notin U$
, it follows that
$0\notin U$
, it follows that
![]() $0\notin U^*$
,
$0\notin U^*$
,
![]() $0\notin U^{**}$
and hence
$0\notin U^{**}$
and hence
![]() $0\notin U^{**<}$
. By Proposition 12.2,
$0\notin U^{**<}$
. By Proposition 12.2,
![]() $U^*$
and
$U^*$
and
![]() $U^{**}$
are directed and hence
$U^{**}$
are directed and hence
![]() $U^{**<}$
is a proper filter containing
$U^{**<}$
is a proper filter containing
![]() $U^{**}$
and hence U. As U is an ultrafilter,
$U^{**}$
and hence U. As U is an ultrafilter,
![]() $U=U^{**}=U^{**<}$
and hence U is a coset, by Proposition 12.3.
$U=U^{**}=U^{**<}$
and hence U is a coset, by Proposition 12.3.
Now suppose that C is another coset with
![]() $(C,U)\in \mathcal {C}^2$
and take any
$(C,U)\in \mathcal {C}^2$
and take any
![]() $c,d\in C$
and
$c,d\in C$
and
![]() $c'\in C^*$
with
$c'\in C^*$
with
![]() $cc'd=d$
. We already saw above that
$cc'd=d$
. We already saw above that
![]() $(CU)^{**}=(cU)^{**}$
is a filter. Extending to an ultrafilter
$(CU)^{**}=(cU)^{**}$
is a filter. Extending to an ultrafilter
![]() $V\supseteq (cU)^{**}$
, we see that
$V\supseteq (cU)^{**}$
, we see that
![]() $(c'V)^{**}$
is another filter containing U, so
$(c'V)^{**}$
is another filter containing U, so
![]() $U=(c'V)^{**}$
by maximality. Then
$U=(c'V)^{**}$
by maximality. Then
![]() $(cU)^{**}=(cc'V)^{**}=V$
, that is,
$(cU)^{**}=(cc'V)^{**}=V$
, that is,
![]() $(CU)^{**}=(cU)^{**}$
was already maximal. Likewise,
$(CU)^{**}=(cU)^{**}$
was already maximal. Likewise,
![]() $(U,C)\in \mathcal {C}^2$
implies that
$(U,C)\in \mathcal {C}^2$
implies that
![]() $(UC)^{**}$
is an ultrafilter, showing that the ultrafilters form an ideal in
$(UC)^{**}$
is an ultrafilter, showing that the ultrafilters form an ideal in
![]() $\mathcal {C}(S)$
.
$\mathcal {C}(S)$
.
It follows that
![]() $\mathcal {U}(S)$
is an étale subgroupoid of
$\mathcal {U}(S)$
is an étale subgroupoid of
![]() $\mathcal {C}(S)$
by [Reference Bice1, Proposition 2.7]. In particular,
$\mathcal {C}(S)$
by [Reference Bice1, Proposition 2.7]. In particular,
![]() $\mathcal {U}(S)$
is locally homeomorphic to its unit space, so to prove that
$\mathcal {U}(S)$
is locally homeomorphic to its unit space, so to prove that
![]() $\mathcal {U}(S)$
is locally Hausdorff it suffices to show that its unit space is Hausdorff. To see this, take any distinct unit ultrafilters
$\mathcal {U}(S)$
is locally Hausdorff it suffices to show that its unit space is Hausdorff. To see this, take any distinct unit ultrafilters
![]() $U,V\in \mathcal {U}(S)$
. By (Multiplicativity),
$U,V\in \mathcal {U}(S)$
. By (Multiplicativity),
![]() $(UV)^<$
is again a filter. By Proposition 8.2, we have
$(UV)^<$
is again a filter. By Proposition 8.2, we have
![]() $m\in U\cap N$
and
$m\in U\cap N$
and
![]() $n\in V\cap N$
. By (
N-Invariance),
$n\in V\cap N$
. By (
N-Invariance),
![]() $U\subseteq (Un)^<\subseteq (UV)^<$
and
$U\subseteq (Un)^<\subseteq (UV)^<$
and
![]() $V\subseteq (mV)^<\subseteq (UV)^<$
. As U and V are distinct and maximal, we must have
$V\subseteq (mV)^<\subseteq (UV)^<$
. As U and V are distinct and maximal, we must have
![]() $(UV)^<=S$
. In particular, we must have
$(UV)^<=S$
. In particular, we must have
![]() $u\in U$
and
$u\in U$
and
![]() $v\in V$
with
$v\in V$
with
![]() $uv<0$
and hence
$uv<0$
and hence
![]() $uv=0$
. Thus,
$uv=0$
. Thus,
![]() $\mathcal {U}_u\cap \mathcal {U}_v=\mathcal {C}_u\cap \mathcal {C}_v\cap \mathcal {U}(S)=\emptyset $
. Indeed, if we had
$\mathcal {U}_u\cap \mathcal {U}_v=\mathcal {C}_u\cap \mathcal {C}_v\cap \mathcal {U}(S)=\emptyset $
. Indeed, if we had
![]() $W\in \mathcal {U}_u\cap \mathcal {U}_v$
then
$W\in \mathcal {U}_u\cap \mathcal {U}_v$
then
![]() $0=uv\in WW=WW^*\subseteq \mathsf {r}(W)=W$
, as W has to be a unit coset, again by Proposition 8.2. But this would mean
$0=uv\in WW=WW^*\subseteq \mathsf {r}(W)=W$
, as W has to be a unit coset, again by Proposition 8.2. But this would mean
![]() $W=0^<=S$
and, in particular,
$W=0^<=S$
and, in particular,
![]() $W\notin \mathcal {U}(S)$
. This shows that the unit space of
$W\notin \mathcal {U}(S)$
. This shows that the unit space of
![]() $\mathcal {U}(S)$
is Hausdorff and hence the entirety of
$\mathcal {U}(S)$
is Hausdorff and hence the entirety of
![]() $\mathcal {U}(S)$
is locally Hausdorff.
$\mathcal {U}(S)$
is locally Hausdorff.
Remark 12.9. We have more to say about
![]() $\mathcal {U}(S)$
in future work. For the moment we simply remark that ultrafilters are more natural to consider than arbitrary filters when dealing with groupoid C*-algebras and more general ‘bumpy semigroups’; see [Reference Bice1, Reference Bice and Clark4].
$\mathcal {U}(S)$
in future work. For the moment we simply remark that ultrafilters are more natural to consider than arbitrary filters when dealing with groupoid C*-algebras and more general ‘bumpy semigroups’; see [Reference Bice1, Reference Bice and Clark4].
12.1 Zakrzewski universality
By Proposition 12.6, the identity embedding of
![]() $\mathcal {D}(S)$
in
$\mathcal {D}(S)$
in
![]() $\mathcal {C}(S)$
is an étale functor. For Zakrzewski universality, we need a Zakrzewski morphism in the opposite direction.
$\mathcal {C}(S)$
is an étale functor. For Zakrzewski universality, we need a Zakrzewski morphism in the opposite direction.
Definition 12.10. For any
![]() $C\in \mathcal {C}(S)$
, we define
$C\in \mathcal {C}(S)$
, we define
So
![]() $\mathrm {dom}(\vartriangleleft )\subseteq \mathcal {C}(S)$
and
$\mathrm {dom}(\vartriangleleft )\subseteq \mathcal {C}(S)$
and
![]() $\mathrm {ran}(\vartriangleleft )\subseteq \mathcal {P}(S)$
. In fact,
$\mathrm {ran}(\vartriangleleft )\subseteq \mathcal {P}(S)$
. In fact,
![]() $\mathrm {ran}(\vartriangleleft )\subseteq \mathcal {D}(S)$
.
$\mathrm {ran}(\vartriangleleft )\subseteq \mathcal {D}(S)$
.
Proposition 12.11. If
![]() $D\vartriangleleft C$
then D is a coset and hence
$D\vartriangleleft C$
then D is a coset and hence
![]() $D\in \mathcal {D}(S)$
. If
$D\in \mathcal {D}(S)$
. If
![]() $\mathcal {D}(S)\ni D\subseteq C\in \mathcal {C}(S)$
then
$\mathcal {D}(S)\ni D\subseteq C\in \mathcal {C}(S)$
then
Moreover, if
![]() $d\in C\in \mathcal {C}(S)$
then we have a unique
$d\in C\in \mathcal {C}(S)$
then we have a unique
![]() $D\in \mathcal {D}(S)$
with
$D\in \mathcal {D}(S)$
with
![]() $d\in D\vartriangleleft C$
.
$d\in D\vartriangleleft C$
.
Proof. If
![]() $D\vartriangleleft C$
then
$D\vartriangleleft C$
then
![]() $C\in \mathcal {C}(S)$
and, in particular,
$C\in \mathcal {C}(S)$
and, in particular,
![]() $C=C^{**}$
. As D is directed, so too are
$C=C^{**}$
. As D is directed, so too are
![]() $D^*$
and
$D^*$
and
![]() $D^{**}$
, by Proposition 12.2. Then (6-2) yields
$D^{**}$
, by Proposition 12.2. Then (6-2) yields
so
![]() $D=D^{**}$
, by maximality. Thus, D is a coset by Proposition 12.3.
$D=D^{**}$
, by maximality. Thus, D is a coset by Proposition 12.3.
Assume that
![]() $d\in C\in \mathcal {C}(S)$
. Taking
$d\in C\in \mathcal {C}(S)$
. Taking
![]() $c,d'\in C$
with
$c,d'\in C$
with
![]() $c<_{d'}d$
, we see that
$c<_{d'}d$
, we see that
![]() $c=cd'd$
and
$c=cd'd$
and
![]() $cd'\in \mathsf {r}(C)\cap N\subseteq (\mathsf {r}(C)\cap N)^<$
(as
$cd'\in \mathsf {r}(C)\cap N\subseteq (\mathsf {r}(C)\cap N)^<$
(as
![]() $\mathsf {r}(C)\cap N$
is directed; see the proof of Proposition 12.7). Thus,
$\mathsf {r}(C)\cap N$
is directed; see the proof of Proposition 12.7). Thus,
![]() $(\mathsf {r}(C)\cap N)^<|d$
so, by Proposition 7.7, we have a coset
$(\mathsf {r}(C)\cap N)^<|d$
so, by Proposition 7.7, we have a coset
with
![]() $\mathsf {r}(D)=\mathsf {r}((\mathsf {r}(C)\cap N)^<)=(\mathsf {r}(C)\cap N)^<$
, by Proposition 12.7. Moreover,
$\mathsf {r}(D)=\mathsf {r}((\mathsf {r}(C)\cap N)^<)=(\mathsf {r}(C)\cap N)^<$
, by Proposition 12.7. Moreover,
because
![]() $\mathsf {r}(C)\cap N\subseteq (\mathsf {r}(C)\cap N)^<\cap N\subseteq \mathsf {r}(C)\cap N$
. Also
$\mathsf {r}(C)\cap N\subseteq (\mathsf {r}(C)\cap N)^<\cap N\subseteq \mathsf {r}(C)\cap N$
. Also
![]() $(\mathsf {r}(C)\cap N)^<d\ni cd'd<_{d'}d$
and hence
$(\mathsf {r}(C)\cap N)^<d\ni cd'd<_{d'}d$
and hence
![]() $d\in D\in \mathcal {D}(S)$
, by Proposition 12.7 and (12-1).
$d\in D\in \mathcal {D}(S)$
, by Proposition 12.7 and (12-1).
We claim that D is actually the largest element of
![]() $\mathcal {D}(S)$
with
$\mathcal {D}(S)$
with
![]() $d\in D\subseteq C$
. To see this, take any other
$d\in D\subseteq C$
. To see this, take any other
![]() $A\in \mathcal {D}(S)$
with
$A\in \mathcal {D}(S)$
with
![]() $d\in A\subseteq C$
. Then
$d\in A\subseteq C$
. Then
![]() $\mathsf {r}(A)$
is directed, by Proposition 12.6, and hence
$\mathsf {r}(A)$
is directed, by Proposition 12.6, and hence
![]() $\mathsf {r}(A)=(\mathsf {r}(A)\cap N)^<\subseteq (\mathsf {r}(C)\cap N)^<=\mathsf {r}(D)$
, by Proposition 12.7. Then (7-2) yields
$\mathsf {r}(A)=(\mathsf {r}(A)\cap N)^<\subseteq (\mathsf {r}(C)\cap N)^<=\mathsf {r}(D)$
, by Proposition 12.7. Then (7-2) yields
proving the claim. Moreover, note that if we had
![]() $\mathsf {r}(A)\cap N=\mathsf {r}(C)\cap N$
then we would have
$\mathsf {r}(A)\cap N=\mathsf {r}(C)\cap N$
then we would have
![]() $\mathsf {r}(A)=(\mathsf {r}(A)\cap N)^<=(\mathsf {r}(C)\cap N)^<=\mathsf {r}(D)$
which would yield
$\mathsf {r}(A)=(\mathsf {r}(A)\cap N)^<=(\mathsf {r}(C)\cap N)^<=\mathsf {r}(D)$
which would yield
![]() $A=D$
above. It follows that D is the unique element of
$A=D$
above. It follows that D is the unique element of
![]() $\mathcal {D}(S)$
with
$\mathcal {D}(S)$
with
![]() $d\in D\vartriangleleft C$
and also the unique element of
$d\in D\vartriangleleft C$
and also the unique element of
![]() $\mathcal {D}(S)$
with
$\mathcal {D}(S)$
with
![]() $d\in D\subseteq C$
and
$d\in D\subseteq C$
and
![]() $\mathsf {r}(C)\cap N=\mathsf {r}(D)\cap N$
, which yields the first
$\mathsf {r}(C)\cap N=\mathsf {r}(D)\cap N$
, which yields the first
![]() $\Leftrightarrow $
in (12-3). The second follows by a dual argument.
$\Leftrightarrow $
in (12-3). The second follows by a dual argument.
Note that the second statement above is saying that any coset C can be partitioned uniquely into maximal directed sub(co)sets. In fact, uniqueness holds even among more general families of directed cosets covering C.
Proposition 12.12. For any
![]() $C\in \mathcal {C}(S)$
,
$C\in \mathcal {C}(S)$
,
is the unique subfamily of
![]() $\mathcal {D}(S)$
with union C and a common source.
$\mathcal {D}(S)$
with union C and a common source.
Proof. Take a family
![]() $\mathscr {D}\subseteq \mathcal {D}(S)$
with
$\mathscr {D}\subseteq \mathcal {D}(S)$
with
![]() $C=\bigcup \mathscr {D}$
. We claim that
$C=\bigcup \mathscr {D}$
. We claim that
 $$ \begin{align} \mathsf{s}(C)\cap N=\bigcup_{D\in\mathscr{D}}\mathsf{s}(D)\cap N. \end{align} $$
$$ \begin{align} \mathsf{s}(C)\cap N=\bigcup_{D\in\mathscr{D}}\mathsf{s}(D)\cap N. \end{align} $$
To see this, take any
![]() $n\in \mathsf {s}(C)\cap N$
. By Proposition 12.11, we have
$n\in \mathsf {s}(C)\cap N$
. By Proposition 12.11, we have
![]() $B\vartriangleleft C$
with
$B\vartriangleleft C$
with
![]() $\mathsf {s}(B)\cap N=\mathsf {s}(C)\cap N$
so
$\mathsf {s}(B)\cap N=\mathsf {s}(C)\cap N$
so
![]() $n\in \mathsf {s}(B)=(B^*B)^<$
, that is, we have
$n\in \mathsf {s}(B)=(B^*B)^<$
, that is, we have
![]() $b\in B$
and
$b\in B$
and
![]() $b'\in B^*$
such that
$b'\in B^*$
such that
![]() $b'b<n$
. Taking
$b'b<n$
. Taking
![]() $e,f\in B$
with
$e,f\in B$
with
![]() $e<_{b'}f$
, directedness yields
$e<_{b'}f$
, directedness yields
![]() $a\in B$
with
$a\in B$
with
![]() $a<b,e$
and hence
$a<b,e$
and hence
![]() $a<_{b'}f$
. As
$a<_{b'}f$
. As
![]() $C=\bigcup \mathscr {D}$
, we have
$C=\bigcup \mathscr {D}$
, we have
![]() $D\in \mathscr {D}$
containing a, so
$D\in \mathscr {D}$
containing a, so
![]() $b\in D$
and
$b\in D$
and
![]() $b'\in D^*$
, which means that
$b'\in D^*$
, which means that
![]() $n\in (D^*D)^<\cap N=\mathsf {s}(D)\cap N$
, proving the claim.
$n\in (D^*D)^<\cap N=\mathsf {s}(D)\cap N$
, proving the claim.
If the directed cosets in
![]() $\mathscr {D}$
also have a common source then the only way (12-4) could hold is if
$\mathscr {D}$
also have a common source then the only way (12-4) could hold is if
![]() $\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
, for all
$\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
, for all
![]() $D\in \mathscr {D}$
. Then Proposition 12.11 again yields
$D\in \mathscr {D}$
. Then Proposition 12.11 again yields
![]() $\mathscr {D}=C^{\vartriangleright } $
, as required.
$\mathscr {D}=C^{\vartriangleright } $
, as required.
If N is diagonal, we can also determine when
![]() $D\vartriangleleft C$
from
$D\vartriangleleft C$
from
![]() $C^Z$
and
$C^Z$
and
![]() $D^Z$
.
$D^Z$
.
Proposition 12.13. For any
![]() $C\in \mathcal {C}(S)$
and
$C\in \mathcal {C}(S)$
and
![]() $D\in \mathcal {D}(S)$
,
$D\in \mathcal {D}(S)$
,
The converse also holds when
![]() $D\subseteq C$
and N is diagonal.
$D\subseteq C$
and N is diagonal.
Proof. Note that
![]() $C^Z=(\mathsf {s}(C)\cap N)^Z$
because, by (9-1),
$C^Z=(\mathsf {s}(C)\cap N)^Z$
because, by (9-1),
Thus, by (12-3),
![]() $D\vartriangleleft C$
implies
$D\vartriangleleft C$
implies
![]() $\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
and hence
$\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
and hence
![]() $C^Z=D^Z$
.
$C^Z=D^Z$
.
Conversely, if N is diagonal,
![]() $D\subseteq C$
and
$D\subseteq C$
and
![]() $C^Z=D^Z$
then Proposition 12.7 yields
$C^Z=D^Z$
then Proposition 12.7 yields
Thus,
![]() $\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
and hence
$\mathsf {s}(C)\cap N=\mathsf {s}(D)\cap N$
and hence
![]() $D\vartriangleleft C$
, by (12-3).
$D\vartriangleleft C$
, by (12-3).
Next, we show that
![]() $\vartriangleleft $
is a Zakrzewski morphism such that the coset representation
$\vartriangleleft $
is a Zakrzewski morphism such that the coset representation
![]() $\mathcal {C}$
factors through the directed coset representation
$\mathcal {C}$
factors through the directed coset representation
![]() $\mathcal {D}$
via preimages of
$\mathcal {D}$
via preimages of
![]() $\vartriangleleft $
.
$\vartriangleleft $
.
Theorem 12.14.
![]() $\vartriangleleft $
is a Zakrzewski morphism from
$\vartriangleleft $
is a Zakrzewski morphism from
![]() $\mathcal {C}(S)$
to
$\mathcal {C}(S)$
to
![]() $\mathcal {D}(S)$
with
$\mathcal {D}(S)$
with
Proof. If
![]() $D\vartriangleleft C$
then
$D\vartriangleleft C$
then
![]() $D^*\vartriangleleft C^*$
. If
$D^*\vartriangleleft C^*$
. If
![]() $D'\vartriangleleft C'$
too and
$D'\vartriangleleft C'$
too and
![]() $\mathsf {s}(C)=\mathsf {r}(C')$
then Proposition 12.7 and (12-3) yield
$\mathsf {s}(C)=\mathsf {r}(C')$
then Proposition 12.7 and (12-3) yield
![]() $\mathsf {s}(D)=(\mathsf {s}(C)\cap N)^<=(\mathsf {r}(C')\cap N)^<=\mathsf {r}(D')$
and
$\mathsf {s}(D)=(\mathsf {s}(C)\cap N)^<=(\mathsf {r}(C')\cap N)^<=\mathsf {r}(D')$
and
so
![]() $D\cdot D'\vartriangleleft C\cdot C'$
. This shows that
$D\cdot D'\vartriangleleft C\cdot C'$
. This shows that
![]() $\vartriangleleft $
is functorial.
$\vartriangleleft $
is functorial.
Now suppose that
![]() $\mathsf {r}(D)\vartriangleleft U$
, for some unit coset U. For any
$\mathsf {r}(D)\vartriangleleft U$
, for some unit coset U. For any
![]() $d\in D$
, we see that
$d\in D$
, we see that
![]() $\mathsf {r}(D)|d$
so
$\mathsf {r}(D)|d$
so
![]() $U|d$
and
$U|d$
and
![]() $D=(\mathsf {r}(D)d)^<\subseteq (Ud)^<$
, as
$D=(\mathsf {r}(D)d)^<\subseteq (Ud)^<$
, as
![]() $\mathsf {r}(D)\subseteq U$
. By Proposition 7.7,
$\mathsf {r}(D)\subseteq U$
. By Proposition 7.7,
![]() $(Ud)^<$
is a coset with
$(Ud)^<$
is a coset with
![]() $\mathsf {r}(Ud)=U$
. Thus,
$\mathsf {r}(Ud)=U$
. Thus,
![]() $\mathsf {r}(D)\cap N=U\cap N=\mathsf {r}(Ud)\cap N$
and hence
$\mathsf {r}(D)\cap N=U\cap N=\mathsf {r}(Ud)\cap N$
and hence
![]() $D\vartriangleleft (Ud)^<$
, by (12-3), showing that
$D\vartriangleleft (Ud)^<$
, by (12-3), showing that
![]() $\vartriangleleft $
is star-surjective. On the other hand, if we had another
$\vartriangleleft $
is star-surjective. On the other hand, if we had another
![]() $C\in \mathcal {C}(S)$
with
$C\in \mathcal {C}(S)$
with
![]() $D\vartriangleleft C$
and
$D\vartriangleleft C$
and
![]() $\mathsf {r}(C)=U$
then
$\mathsf {r}(C)=U$
then
![]() $C=(\mathsf {r}(C)d)^<=(Ud)^<$
, as
$C=(\mathsf {r}(C)d)^<=(Ud)^<$
, as
![]() $d\in D\subseteq C$
, showing that
$d\in D\subseteq C$
, showing that
![]() $\vartriangleleft $
is also star-injective.
$\vartriangleleft $
is also star-injective.
Lastly, note that if
![]() $\mathcal {D}_a\ni D\vartriangleleft C$
then certainly
$\mathcal {D}_a\ni D\vartriangleleft C$
then certainly
![]() $C\in \mathcal {C}_a$
, while conversely if
$C\in \mathcal {C}_a$
, while conversely if
![]() $C\in \mathcal {C}_a$
then Proposition 12.11 yields
$C\in \mathcal {C}_a$
then Proposition 12.11 yields
![]() $D\in \mathcal {D}_a$
with
$D\in \mathcal {D}_a$
with
![]() $D\vartriangleleft C$
. This shows that
$D\vartriangleleft C$
. This shows that
![]() $\vartriangleleft ^{-1}[\mathcal {D}_a]=\mathcal {C}_a$
, so
$\vartriangleleft ^{-1}[\mathcal {D}_a]=\mathcal {C}_a$
, so
![]() $\vartriangleleft $
is also continuous and hence a Zakrzewski morphism satisfying (12-6).
$\vartriangleleft $
is also continuous and hence a Zakrzewski morphism satisfying (12-6).
We call an étale representation
![]() $\mu :S\rightarrow \mathcal {B}(G)$
Zakrzewski universal if, for every étale representation
$\mu :S\rightarrow \mathcal {B}(G)$
Zakrzewski universal if, for every étale representation
![]() $\theta :S\rightarrow \mathcal {B}(H)$
, there exists a unique Zakrzewski morphism
$\theta :S\rightarrow \mathcal {B}(H)$
, there exists a unique Zakrzewski morphism
![]() $\phi \subseteq G\times H$
such that
$\phi \subseteq G\times H$
such that
![]() $\theta =\overline \phi \circ \mu $
, where
$\theta =\overline \phi \circ \mu $
, where
![]() $\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
is the preimage map.
$\overline \phi :\mathcal {B}(G)\rightarrow \mathcal {B}(H)$
is the preimage map.
Theorem 12.15. If Z is symmetric then the directed coset representation
![]() $\mathcal {D}$
is a Zakrzewski universal étale representation.
$\mathcal {D}$
is a Zakrzewski universal étale representation.
Proof. As
![]() $\mathcal {C}$
is an étale representation by Theorem 8.11, and
$\mathcal {C}$
is an étale representation by Theorem 8.11, and
![]() $\mathcal {D}(S)$
is an ideal of
$\mathcal {D}(S)$
is an ideal of
![]() $\mathcal {C}(S)$
by Proposition 12.6, it follows that
$\mathcal {C}(S)$
by Proposition 12.6, it follows that
![]() $\mathcal {D}$
is also an étale representation.
$\mathcal {D}$
is also an étale representation.
To see that
![]() $\mathcal {D}$
is Zakrzewski universal, let us take another étale representation
$\mathcal {D}$
is Zakrzewski universal, let us take another étale representation
![]() $\theta :S\rightarrow \mathcal {B}(G)$
. Let
$\theta :S\rightarrow \mathcal {B}(G)$
. Let
![]() $\phi $
be the étale morphism in the proof of Theorem 8.11 given by
$\phi $
be the étale morphism in the proof of Theorem 8.11 given by
By Theorem 12.14,
![]() $\vartriangleleft $
is also a Zakrzewski morphism and hence so is the composition
$\vartriangleleft $
is also a Zakrzewski morphism and hence so is the composition
Moreover,
![]() $\overline {\psi }\circ \mathcal {D}=\overline {\phi }\circ \overline {\vartriangleleft }\circ \mathcal {D}=\overline {\phi }\circ \mathcal {C}=\theta $
, by (12-6) and the proof of Theorem 8.11.
$\overline {\psi }\circ \mathcal {D}=\overline {\phi }\circ \overline {\vartriangleleft }\circ \mathcal {D}=\overline {\phi }\circ \mathcal {C}=\theta $
, by (12-6) and the proof of Theorem 8.11.
The only thing left to prove is that
![]() $\psi $
is unique. Accordingly, suppose that we had another Zakrzewski morphism
$\psi $
is unique. Accordingly, suppose that we had another Zakrzewski morphism
![]() $\psi '\subseteq \mathcal {D}(S)\times G$
with
$\psi '\subseteq \mathcal {D}(S)\times G$
with
![]() $\overline {\psi '}\circ \mathcal {D}=\theta $
, that is,
$\overline {\psi '}\circ \mathcal {D}=\theta $
, that is,
![]() ${\psi ^{\prime -1}[\mathcal {D}_a]=\theta (a)}$
, for all
${\psi ^{\prime -1}[\mathcal {D}_a]=\theta (a)}$
, for all
![]() $a\in S$
. Then we see that
$a\in S$
. Then we see that
![]() $g\in \theta (a)$
if and only if
$g\in \theta (a)$
if and only if
![]() $D\ \psi '\ g$
, for some
$D\ \psi '\ g$
, for some
![]() $D\in \mathcal {D}_a$
, and hence
$D\in \mathcal {D}_a$
, and hence
 $$ \begin{align*} \bigcup_{D\,\psi'\,g}D=\{a\in S:g\in\theta(a)\}=\phi(g). \end{align*} $$
$$ \begin{align*} \bigcup_{D\,\psi'\,g}D=\{a\in S:g\in\theta(a)\}=\phi(g). \end{align*} $$
As
![]() $\psi '$
is a functorial relation, all those
$\psi '$
is a functorial relation, all those
![]() $D\in \mathcal {D}(S)$
with
$D\in \mathcal {D}(S)$
with
![]() $D\,\psi '\,g$
must have a common source. By Proposition 12.12, it follows that
$D\,\psi '\,g$
must have a common source. By Proposition 12.12, it follows that
This shows that
![]() $\psi '=\psi $
, as required.
$\psi '=\psi $
, as required.
As in Proposition 4.8, we can consider the pullback bundle
 $$ \begin{align*} \rho_{\mathcal{D}}^{\vartriangleleft} :\mathop{\vartriangleleft^{\rho_{\mathcal{D}}}}\widetilde{\mathcal{D}}(S)\rightarrow\mathcal{C}(S), \end{align*} $$
$$ \begin{align*} \rho_{\mathcal{D}}^{\vartriangleleft} :\mathop{\vartriangleleft^{\rho_{\mathcal{D}}}}\widetilde{\mathcal{D}}(S)\rightarrow\mathcal{C}(S), \end{align*} $$
which is continuously isomorphic to the coset bundle
 $\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
.
$\rho _{\mathcal {C}}:\widetilde {\mathcal {C}}(S)\rightarrow \mathcal {C}(S)$
.
Proposition 12.16. Whenever
![]() $d\in D\vartriangleleft C$
, we can define
$d\in D\vartriangleleft C$
, we can define
The resulting function is a continuous isomorphism
 $\iota :\mathop {\vartriangleleft ^{\rho _{\mathcal {D}}}}\widetilde {\mathcal {D}}(S)\rightarrow \widetilde {\mathcal {C}}(S)$
.
$\iota :\mathop {\vartriangleleft ^{\rho _{\mathcal {D}}}}\widetilde {\mathcal {D}}(S)\rightarrow \widetilde {\mathcal {C}}(S)$
.
Proof. If
![]() $d\in D\vartriangleleft C$
then
$d\in D\vartriangleleft C$
then
![]() $C^Z=D^Z$
and
$C^Z=D^Z$
and
![]() ${}^ZC={}^ZD$
, by (12-5), so
${}^ZC={}^ZD$
, by (12-5), so
![]() $d^{\sim _C}=d^{\sim _D}$
, by (9-4). In particular,
$d^{\sim _C}=d^{\sim _D}$
, by (9-4). In particular,
![]() $\iota $
is well-defined. Whenever
$\iota $
is well-defined. Whenever
![]() $d\in C\in \mathcal {C}(S)$
, Proposition 12.11 yields a unique
$d\in C\in \mathcal {C}(S)$
, Proposition 12.11 yields a unique
![]() $D\vartriangleleft C$
with
$D\vartriangleleft C$
with
![]() $d\in D$
. This shows that
$d\in D$
. This shows that
![]() $\iota $
is a bijection, which is immediately seen to be a groupoid isomorphism. Moreover, for all
$\iota $
is a bijection, which is immediately seen to be a groupoid isomorphism. Moreover, for all
![]() $s\in S$
, we see that
$s\in S$
, we see that
 $\iota ^{-1}[\widetilde {\mathcal {C}}_s]=\rho _{\mathcal {D}}^{\vartriangleleft -1}[\mathcal {C}_s]$
and
$\iota ^{-1}[\widetilde {\mathcal {C}}_s]=\rho _{\mathcal {D}}^{\vartriangleleft -1}[\mathcal {C}_s]$
and
 ${\iota ^{-1}[\widetilde {\mathcal {C}}^s]=\mathop {\vartriangleleft ^{\rho _{\mathcal {D}}}}\widetilde {\mathcal {D}}(S)\cap (\widetilde {\mathcal {D}}^s\times \mathcal {C}_s)}$
, so
${\iota ^{-1}[\widetilde {\mathcal {C}}^s]=\mathop {\vartriangleleft ^{\rho _{\mathcal {D}}}}\widetilde {\mathcal {D}}(S)\cap (\widetilde {\mathcal {D}}^s\times \mathcal {C}_s)}$
, so
![]() $\iota $
is also continuous.
$\iota $
is also continuous.
We now have the following extension of Theorem 12.14. As before, let
![]() $\widetilde {\mathcal {C}}$
and
$\widetilde {\mathcal {C}}$
and
![]() $\widetilde {\mathcal {D}}$
denote the maps
$\widetilde {\mathcal {D}}$
denote the maps
![]() $a\mapsto \widetilde {a}=\widetilde {a}_{\mathcal {C}}$
and
$a\mapsto \widetilde {a}=\widetilde {a}_{\mathcal {C}}$
and
![]() $a\mapsto \widetilde {a}_{\mathcal {D}}=\widetilde {a}|_{\mathcal {D}(S)}$
, respectively.
$a\mapsto \widetilde {a}_{\mathcal {D}}=\widetilde {a}|_{\mathcal {D}(S)}$
, respectively.
Corollary 12.17.
![]() $(\vartriangleleft ,\iota )$
is a Zakrzewski–Pierce morphism from
$(\vartriangleleft ,\iota )$
is a Zakrzewski–Pierce morphism from
![]() $\rho _{\mathcal {D}}$
to
$\rho _{\mathcal {D}}$
to
![]() $\rho _{\mathcal {C}}$
such that
$\rho _{\mathcal {C}}$
such that
 $$ \begin{align*} \widetilde{\mathcal{C}}=\frac{\iota}{\vartriangleleft}\circ\widetilde{\mathcal{D}}, \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{C}}=\frac{\iota}{\vartriangleleft}\circ\widetilde{\mathcal{D}}, \end{align*} $$
where
![]() ${\iota }/{\vartriangleleft }:\mathcal {S}(\rho _{\mathcal {D}})\rightarrow \mathcal {S}(\rho _{\mathcal {C}})$
is the semigroup morphism from Theorem 4.10.
${\iota }/{\vartriangleleft }:\mathcal {S}(\rho _{\mathcal {D}})\rightarrow \mathcal {S}(\rho _{\mathcal {C}})$
is the semigroup morphism from Theorem 4.10.
Proof. By Theorem 12.14 and Proposition 12.16,
![]() $(\vartriangleleft ,\iota )$
is a Zakrzewski–Pierce morphism. For any
$(\vartriangleleft ,\iota )$
is a Zakrzewski–Pierce morphism. For any
![]() $C\in \mathrm {dom}(\widetilde {a}_{\mathcal {C}})=\mathcal {C}_a$
, we have a unique
$C\in \mathrm {dom}(\widetilde {a}_{\mathcal {C}})=\mathcal {C}_a$
, we have a unique
![]() $D\in \mathcal {D}(S)$
with
$D\in \mathcal {D}(S)$
with
![]() $a\in D\vartriangleleft C$
, by Proposition 12.11. Then we see that
$a\in D\vartriangleleft C$
, by Proposition 12.11. Then we see that
 $$ \begin{align*} \widetilde{a}_{\mathcal{C}}(C)=[a,C]=\iota([a,D],C)= \iota((\widetilde{a}_{\mathcal{D}}\circ\!\vartriangleleft)(C),C)=\frac{\iota}{\vartriangleleft}(\widetilde{a}_{\mathcal{D}})(C). \end{align*} $$
$$ \begin{align*} \widetilde{a}_{\mathcal{C}}(C)=[a,C]=\iota([a,D],C)= \iota((\widetilde{a}_{\mathcal{D}}\circ\!\vartriangleleft)(C),C)=\frac{\iota}{\vartriangleleft}(\widetilde{a}_{\mathcal{D}})(C). \end{align*} $$
This shows that
![]() $\widetilde {a}_{\mathcal {C}}=({\iota }/{\vartriangleleft })(\widetilde {a}_{\mathcal {D}})$
, which in turn shows that
$\widetilde {a}_{\mathcal {C}}=({\iota }/{\vartriangleleft })(\widetilde {a}_{\mathcal {D}})$
, which in turn shows that
 $\widetilde {\mathcal {C}}=({\iota }/{\vartriangleleft })\circ \widetilde {\mathcal {D}}$
.
$\widetilde {\mathcal {C}}=({\iota }/{\vartriangleleft })\circ \widetilde {\mathcal {D}}$
.
Again, we call a bundle representation
![]() $\mu :S\rightarrow \mathcal {S}(\pi )$
Zakrzewski universal if, for every bundle representation
$\mu :S\rightarrow \mathcal {S}(\pi )$
Zakrzewski universal if, for every bundle representation
![]() $\theta :S\rightarrow \mathcal {S}(\pi ')$
, there exists a unique Zakrzewski–Pierce morphism
$\theta :S\rightarrow \mathcal {S}(\pi ')$
, there exists a unique Zakrzewski–Pierce morphism
![]() $(\phi ,\tau )$
from
$(\phi ,\tau )$
from
![]() $\pi $
to
$\pi $
to
![]() $\pi '$
such that
$\pi '$
such that
![]() $\theta =({\tau }/{\phi })\circ \mu $
.
$\theta =({\tau }/{\phi })\circ \mu $
.
Theorem 12.18. If Z is symmetric then the directed coset bundle representation
![]() $\widetilde {\mathcal {D}}$
is a Zakrzewski universal bundle representation.
$\widetilde {\mathcal {D}}$
is a Zakrzewski universal bundle representation.
Proof. As
![]() $\widetilde {\mathcal {C}}$
is a bundle representation by Theorem 11.2, and
$\widetilde {\mathcal {C}}$
is a bundle representation by Theorem 11.2, and
![]() $\mathcal {D}(S)$
is an ideal of
$\mathcal {D}(S)$
is an ideal of
![]() $\mathcal {C}(S)$
by Proposition 12.6, it follows that
$\mathcal {C}(S)$
by Proposition 12.6, it follows that
![]() $\widetilde {\mathcal {D}}$
is also a bundle representation.
$\widetilde {\mathcal {D}}$
is also a bundle representation.
To see that
![]() $\widetilde {\mathcal {D}}$
is Zakrzewski universal, let us take another bundle representation
$\widetilde {\mathcal {D}}$
is Zakrzewski universal, let us take another bundle representation
![]() $\theta :S\rightarrow \mathcal {S}(\pi )$
. Let
$\theta :S\rightarrow \mathcal {S}(\pi )$
. Let
![]() $\psi =\ \vartriangleleft \circ \,\phi $
be the Zakrzewski morphism in the proof of Theorem 12.15, where
$\psi =\ \vartriangleleft \circ \,\phi $
be the Zakrzewski morphism in the proof of Theorem 12.15, where
![]() $\phi $
is the étale morphism in the proof of Theorem 8.11 given by
$\phi $
is the étale morphism in the proof of Theorem 8.11 given by
![]() $\phi (g)=\{a\in S:g\in \theta (a)\}$
. Further, let
$\phi (g)=\{a\in S:g\in \theta (a)\}$
. Further, let
 $\tau :\phi ^{\pi }\widetilde {\mathcal {C}}(S)\rightarrow F$
be the continuous functor in the proof of Theorem 11.2 given by
$\tau :\phi ^{\pi }\widetilde {\mathcal {C}}(S)\rightarrow F$
be the continuous functor in the proof of Theorem 11.2 given by
![]() $\tau ([a,\phi (g)],g)=\theta (a)(g)$
. We then get another continuous functor
$\tau ([a,\phi (g)],g)=\theta (a)(g)$
. We then get another continuous functor
 $\sigma :\psi ^{\rho _{\mathcal {D}}}\widetilde {\mathcal {D}}(S)\rightarrow F$
defined by
$\sigma :\psi ^{\rho _{\mathcal {D}}}\widetilde {\mathcal {D}}(S)\rightarrow F$
defined by
whenever
![]() $a\in D\vartriangleleft \phi (g)$
. Thus,
$a\in D\vartriangleleft \phi (g)$
. Thus,
![]() $(\psi ,\sigma )$
is a Zakrzewski–Pierce morphism with
$(\psi ,\sigma )$
is a Zakrzewski–Pierce morphism with
 $$ \begin{align*} \frac{\sigma}{\psi}(\widetilde{a}_{\mathcal{D}})(g)=\sigma((\widetilde{a}_{\mathcal{D}}\circ\psi)(g),g)=\sigma([a,D],g)=\theta(a)(g), \end{align*} $$
$$ \begin{align*} \frac{\sigma}{\psi}(\widetilde{a}_{\mathcal{D}})(g)=\sigma((\widetilde{a}_{\mathcal{D}}\circ\psi)(g),g)=\sigma([a,D],g)=\theta(a)(g), \end{align*} $$
where D is the unique directed coset with
![]() $a\in D\vartriangleleft \phi (g)$
. This shows that
$a\in D\vartriangleleft \phi (g)$
. This shows that
![]() $({\sigma }/{\psi })(\widetilde {a}_{\mathcal {D}})=\theta (a)$
, which in turn shows that
$({\sigma }/{\psi })(\widetilde {a}_{\mathcal {D}})=\theta (a)$
, which in turn shows that
 $\theta =({\sigma }/{\psi })\circ \widetilde {\mathcal {D}}$
.
$\theta =({\sigma }/{\psi })\circ \widetilde {\mathcal {D}}$
.
For uniqueness, suppose that we had another Zakrzewski–Pierce morphism
![]() $(\psi ',\sigma ')$
with
$(\psi ',\sigma ')$
with
 $\theta =({\sigma '}/{\psi '})\circ \widetilde {\mathcal {D}}$
. By Theorem 12.15, we must have
$\theta =({\sigma '}/{\psi '})\circ \widetilde {\mathcal {D}}$
. By Theorem 12.15, we must have
![]() $\psi '=\psi $
. For any
$\psi '=\psi $
. For any
 $([a,D],g)\in \psi ^{\rho _{\mathcal {D}}}\widetilde {\mathcal {D}}(S)$
,
$([a,D],g)\in \psi ^{\rho _{\mathcal {D}}}\widetilde {\mathcal {D}}(S)$
,
 $$ \begin{align*} \sigma'([a,D],g)=\frac{\sigma'}{\psi'}(\widetilde{a}_{\mathcal{D}})(g)=\theta(a)(g)=\sigma([a,D],g). \end{align*} $$
$$ \begin{align*} \sigma'([a,D],g)=\frac{\sigma'}{\psi'}(\widetilde{a}_{\mathcal{D}})(g)=\theta(a)(g)=\sigma([a,D],g). \end{align*} $$
Thus,
![]() $\sigma '=\sigma $
, proving uniqueness and hence universality.
$\sigma '=\sigma $
, proving uniqueness and hence universality.
As in Corollary 11.3, it follows that even directed cosets and their equivalence classes determine when structured semigroups have faithful bundle representations.
Corollary 12.19. If Z is symmetric then the following assertions are equivalent.
(1)
 $(S,N,Z)$
has a faithful bundle representation.
$(S,N,Z)$
has a faithful bundle representation.(2) The directed coset bundle representation of
 $(S,N,Z)$
is faithful.
$(S,N,Z)$
is faithful.(3) For all distinct
 $a,b\in S$
, we have
$a,b\in S$
, we have
 $D\in \mathcal {D}(S)$
with
$D\in \mathcal {D}(S)$
with
 $\{a,b\}\cap D\neq \emptyset $
and
$\{a,b\}\cap D\neq \emptyset $
and  $$ \begin{align*} a\not\sim_Db. \end{align*} $$
$$ \begin{align*} a\not\sim_Db. \end{align*} $$
Acknowledgement
Many thanks to the anonymous referee for reading the first draft very carefully and making numerous helpful comments and suggestions which have been incorporated into this final version.



