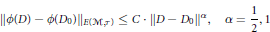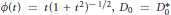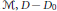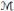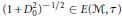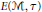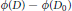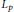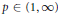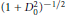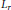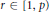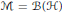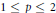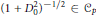1 results
Operator Estimates for Fredholm Modules
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 4 / 01 August 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 849-896
- Print publication:
- 01 August 2000
-
- Article
-
- You have access
- Export citation
-
We study estimates of the type
1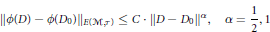
$${{\left\| \phi (D)\,-\,\phi ({{D}_{0}}) \right\|}_{E(\mathcal{M},\,\tau )}}\,\le \,C\,\cdot \,{{\left\| D\,-\,{{D}_{0}} \right\|}^{\alpha }},\,\,\,\,\,\,\,\alpha \,=\,\frac{1}{2},\,1$$where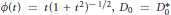
$\phi (t)\,=\,t{{(1\,+\,{{t}^{2}})}^{-1/2}},\,{{D}_{0}}\,=\,D_{0}^{*}$ is an unbounded linear operator affiliated with a semifinite von Neumann algebra 
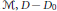$M,D-{{D}_{0}}$ is a bounded self-adjoint linear operator from 
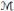$\mathcal{M}$ and 
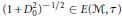${{(1+D_{0}^{2})}^{-1/2}}\in E(M,\tau )$, where 
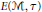$E(\mathcal{M},\tau )$ is a symmetric operator space associated with 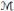$\mathcal{M}$. In particular, we prove that 
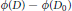$\phi \left( D \right)-\phi \left( {{D}_{0}} \right)$ belongs to the non-commutative 
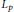${{L}_{p}}$-space for some 
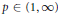$p\in (1,\infty )$, provided 
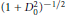${{(1+D_{0}^{2})}^{-1/2}}$ belongs to the noncommutative weak 
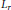${{L}_{r}}$-space for some 
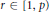$r\in [1,p)$. In the case 
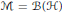$\mathcal{M}\,=\,\mathcal{B}\left( \mathcal{H} \right)$ and 
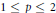$1\,\le \,p\,\le \,2$, we show that this result continues to hold under the weaker assumption 
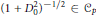${{(1+D_{0}^{2})}^{-1/2}}\in {{C}_{p}}$. This may be regarded as an odd counterpart of A. Connes’ result for the case of even Fredholm modules.
