Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T16:27:46.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Operator Estimates for Fredholm Modules

Published online by Cambridge University Press:  20 November 2018

F. A. Sukochev
F. A. Sukochev*
Affiliation:
Department of Mathematics and Statistics, The Flinders University of South Australia, GPO Box 2100, Adelaide, SA 5001, Australia email: sukochev@ist.flinders.edu.au Department of Pure Mathematics, The University of Adelaide, Adelaide, SA 5005, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study estimates of the type

1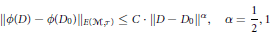

$${{\left\| \phi (D)\,-\,\phi ({{D}_{0}}) \right\|}_{E(\mathcal{M},\,\tau )}}\,\le \,C\,\cdot \,{{\left\| D\,-\,{{D}_{0}} \right\|}^{\alpha }},\,\,\,\,\,\,\,\alpha \,=\,\frac{1}{2},\,1$$

where $\phi (t)\,=\,t{{(1\,+\,{{t}^{2}})}^{-1/2}},\,{{D}_{0}}\,=\,D_{0}^{*}$ is an unbounded linear operator affiliated with a semifinite von Neumann algebra $M,D-{{D}_{0}}$ is a bounded self-adjoint linear operator from 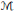$\mathcal{M}$ and 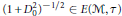${{(1+D_{0}^{2})}^{-1/2}}\in E(M,\tau )$, where 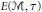$E(\mathcal{M},\tau )$ is a symmetric operator space associated with 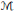$\mathcal{M}$. In particular, we prove that 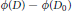$\phi \left( D \right)-\phi \left( {{D}_{0}} \right)$ belongs to the non-commutative 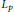${{L}_{p}}$-space for some 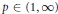$p\in (1,\infty )$, provided 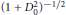${{(1+D_{0}^{2})}^{-1/2}}$ belongs to the noncommutative weak 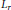${{L}_{r}}$-space for some 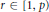$r\in [1,p)$. In the case 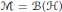$\mathcal{M}\,=\,\mathcal{B}\left( \mathcal{H} \right)$ and 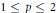$1\,\le \,p\,\le \,2$, we show that this result continues to hold under the weaker assumption 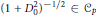${{(1+D_{0}^{2})}^{-1/2}}\in {{C}_{p}}$. This may be regarded as an odd counterpart of A. Connes’ result for the case of even Fredholm modules.

Keywords

46L5046E3046L8747A5558B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 4 , 01 August 2000 , pp. 849 - 896
Copyright
Copyright © Canadian Mathematical Society 2000

References

[An] Ando, T., Comparison of norms ∥f (A)− f (B)∥ and ∥ f (|A|)− f (|B|)∥. Math. Z. 197(1988), 403–409.Google Scholar
[Ar] Arazy, J., Some remarks on interpolation theorems and the boundedness of the triangular projection in unitary matrix spaces. Integral Equations Operator Theory 1(1978), 453–495.Google Scholar
[BKS] Birman, M. S., Koplienko, L. S. and Solomyak, M. Z., Estimates for the spectrumof the difference between fractional powers of two selfadjoint operators. (Russian) Izvestia VUZ (3) 154(1975), 3–10.Google Scholar
[BM] Braverman, M. and Mekler, A., The Hardy-Littlewood property for symmetric spaces. (Russian) Sib.Mat. Zhur. 18(1977), 522–540.Google Scholar
[BR] Bennett, C. and Rudnick, K., On Lorentz-Zygmund spaces. Dissertationes Math. 175(1980), 5–67.Google Scholar
[BS] Bennett, C. and Sharpley, R., Interpolation of operators. Pure Appl. Math. 129, 1988.Google Scholar
[BSo1–3] Birman, M. Sh. and Solomyak, M. Z., Double Stilties operator integrals I; II; III. Problemy Mat. Fiz. 1(1966), 33–67. 2 (1967), 26–60; 6(1973), 27–53.Google Scholar
[CP] Carey, A. and Phillips, J., Unbounded Fredholm modules and spectral flow. Canad. J. Math. 50(1998), 673–718.Google Scholar
[Co1] Connes, A., Noncommutative differential geometry. Publ.Math. Inst. Hautes Études Sci. 62(1985), 41–144.Google Scholar
[Co2] Connes, A., Noncommutative geometry. Academic Press, 1994.Google Scholar
[CS] Chilin, V. I. and Sukochev, F. A., Weak convergence in non-commutative symmetric spaces. J. Operator Theory 31(1994), 35–65.Google Scholar
[Da] Davies, E. B., Lipschitz continuity of functions of operators in the Schatten classes. J. LondonMath. Soc. 37(1988), 148–157.Google Scholar
[DD] Dodds, P. G. and Dodds, T. K., On submajorization inequality of T. Ando. Oper. Theory Adv. Appl. 75(1995), 113–133.Google Scholar
[DDP1] Dodds, P. G., Dodds, T. K. and de Pagter, B., Non-commutative Banach function spaces. Math. Z. 201(1989), 583–597.Google Scholar
[DDP2] Dodds, P. G., Dodds, T. K. and de Pagter, B., Non-commutative Köthe duality. Trans. Amer.Math. Soc. 339(1993), 717–750.Google Scholar
[DDPS1] Dodds, P. G., Dodds, T. K., de Pagter, B. and Sukochev, F. A., Lipschitz continuity of the absolute value and Riesz projection in symmetric operator spaces. J. Funct. Anal. 148(1997), 28–69.Google Scholar
[DDPS2] Dodds, P. G., Dodds, T. K., de Pagter, B. and Sukochev, F. A., Lipschitz continuity of the absolute value in preduals of semifinite factors. Integral Equations Operator Theory 34(1999), 28–44.Google Scholar
[FK] Fack, T. and Kosaki, H., Generalized s-numbers of τ -measurable operators. Pacific J. Math. 123(1986), 269–300.Google Scholar
[HN] Hiai, F. and Nakamura, Y., Distance between unitary orbits in von Neumann algebras. Pacific J. Math. 138(1989), 259–294.Google Scholar
[Ka] Kaminska, A., Some remarks on Orlicz-Lorentz spaces. Math. Nachr. 147(1989), 29–38.Google Scholar
[Ko] Kosaki, H., Unitarily invariant norms under which the map A |A|is continuous. Publ. Res. Inst. Math. Sci. 28(1992), 299–313.Google Scholar
[KPS] Krein, S. G., Petunin, Ju. I. and Semenov, E. M., Interpolation of linear operators. Transl. Math. Monographs 54, Amer.Math. Soc., 1982.Google Scholar
[KR] Krasnoselskii, M. A. and Rutickii, Ya. B., Convex functions and Orlicz spaces. P. Noordhoff, Groningen, 1961.Google Scholar
[LT2] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces II. Springer-Verlag, 1979.Google Scholar
[Ne] Nelson, E., Notes on non-commutative integration. J. Funct. Anal. 15(1974), 103–116.Google Scholar
[O1] Ovchinnikov, V. I., Symmetric spaces of measurable operators. Soviet Math. Dokl. 11(1970), 448–451.Google Scholar
[O2] Ovchinnikov, V. I., Symmetric spaces of measurable operators. (Russian) Trudy Inst.Mat. VGU 3(1971), 88–107.Google Scholar
[P1] Phillips, J., Self-adjoint Fredholm operators and spectral flow. Canad. Math. Bull. 39(1996), 460–467.Google Scholar
[P2] Phillips, J., Spectral flow in type I and II factors—Anew approach. Fields Inst. Commun. 17(1997), 137–153.Google Scholar
[SC] Sukochev, F. A. and Chilin, V. I., Symmetric spaces on semifinite von Neumann algebras. Soviet Math. Dokl. 42(1991), 97–101.Google Scholar
[SSS] Sedaev, A. A., Semenov, E. M. and Sukochev, F. A., Perturbation estimate of the operator function D(1 + D2)−1/2 in symmetric spaces via a certain nonlinear functional. (Russian) Dokl. Akad. Nauk 369(1999), 316–319.Google Scholar
[Te] Terp, M., Lp-spaces associated with von Neumann algebras. Notes, Copenhagen University, 1981.Google Scholar