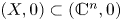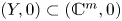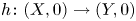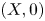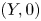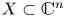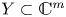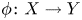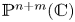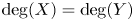In this paper, we prove the Fukui–Kurdyka–Paunescu conjecture, which says that sub-analytic arc-analytic bi-Lipschitz homeomorphisms preserve the multiplicities of real analytic sets. We also prove several other results on the invariance of the multiplicity (respectively, degree) of real and complex analytic (respectively, algebraic) sets. For instance, still in the real case, we prove a global version of the Fukui–Kurdyka–Paunescu conjecture. In the complex case, one of the results that we prove is the following: if 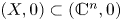$(X,0)\subset (\mathbb {C}^{n},0)$, 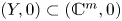$(Y,0)\subset (\mathbb {C}^{m},0)$ are germs of analytic sets and 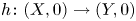$h\colon (X,0)\to (Y,0)$ is a semi-bi-Lipschitz homeomorphism whose graph is a complex analytic set, then the germs 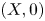$(X,0)$ and 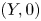$(Y,0)$ have the same multiplicity. One of the results that we prove in the global case is the following: if 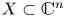$X\subset \mathbb {C}^{n}$, 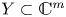$Y\subset \mathbb {C}^{m}$ are algebraic sets and 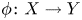$\phi \colon X\to Y$ is a semi-algebraic semi-bi-Lipschitz homeomorphism such that the closure of its graph in 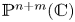$\mathbb {P}^{n+m}(\mathbb {C})$ is an orientable homological cycle, then 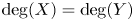${\rm deg}(X)={\rm deg}(Y)$.

It is proved that flatness of an analytic mapping germ from a complete intersection is determined by its sufficiently high jet. As a consequence, one obtains finite determinacy of complete intersections. It is also shown that flatness and openness are stable under deformations.

Let G be a Lie group, and let M be a smooth proper G-manifold. Let M/G denote the orbit space, and let π : M → M/G be the natural map. It is known that M/G is homeomorphic to a polyhedron. In the present paper we show that there exist a piecewise linear (PL) manifold P, a polyhedron L, and homeomorphisms τ : P → M and σ : M/G → L such that σ o π o τ is PL. This is an application of the theory of subanalytic sets and subanalytic maps of Shiota. If M and the G-action are, moreover, subanalytic, then we can choose τ and σ subanalytic and P and L unique up to PL homeomorphisms.

We give an explicit formula for the projective dynamics of planar homogeneous polynomial differential systems in terms of natural local invariants and we establish explicit algebraic connections (syzygies) between these invariants (leading to restrictions on possible global dynamics). We discuss multidimensional generalizations together with applications to the existence of first integrals and bounded solutions.