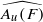 $_0$ WITH PRESCRIBED ASSOCIATED FLOW
$_0$ WITH PRESCRIBED ASSOCIATED FLOW
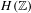 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
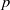 $p$-HARMONIC BOUNDARY AND
$p$-HARMONIC BOUNDARY AND 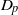 ${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE