Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T16:32:40.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-triviality of the Poisson boundary of random walks on the group 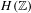$H(\mathbb{Z})$ of Monod

Part of: Markov processes Probability theory on algebraic and topological structures Special aspects of infinite or finite groups Graph theory

Published online by Cambridge University Press:  04 November 2019

BOGDAN STANKOV Open the ORCID record for BOGDAN STANKOV [Opens in a new window]
BOGDAN STANKOV*
Affiliation:
Département de mathématiques et applications, École normale supérieure, CNRS, PSL Research University, 75005Paris, France email bogdan.zl.stankov@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We give sufficient conditions for the non-triviality of the Poisson boundary of random walks on 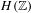$H(\mathbb{Z})$ and its subgroups. The group 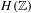$H(\mathbb{Z})$ is the group of piecewise projective homeomorphisms over the integers defined by Monod [Groups of piecewise projective homeomorphisms. Proc. Natl Acad. Sci. USA110(12) (2013), 4524–4527]. For a finitely generated subgroup 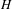$H$ of 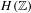$H(\mathbb{Z})$, we prove that either 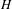$H$ is solvable or every measure on 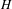$H$ with finite first moment that generates it as a semigroup has non-trivial Poisson boundary. In particular, we prove the non-triviality of the Poisson boundary of measures on Thompson’s group $F$ that generate it as a semigroup and have finite first moment, which answers a question by Kaimanovich [Thompson’s group $F$ is not Liouville. Groups, Graphs and Random Walks (London Mathematical Society Lecture Note Series). Eds. T. Ceccherini-Silberstein, M. Salvatori and E. Sava-Huss. Cambridge University Press, Cambridge, 2017, pp. 300–342, 7.A].

Keywords

Random walks on groupsPoisson boundarySchreier graphThompson’s group Fsolvable group

MSC classification

Primary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization 05C81: Random walks on graphs
Secondary: 20F65: Geometric group theory 60J05: Discrete-time Markov processes on general state spaces 60J50: Boundary theory 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 4 , April 2021 , pp. 1160 - 1189
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adyan, S. I.. Random walks on free periodic groups. Izv. Akad. Nauk SSSR Ser. Mat. 46(6) (1982), 1139–1149, 1343.Google Scholar
Avez, A.. Entropie des groupes de type fini. C. R. Acad. Sci. Paris, Sér. A 275 (1972), 1363–1366.Google Scholar
Baldi, P., Lohoué, N. and Peyrière, J.. Sur la classification des groupes récurrents. C. R. Acad. Sci. Paris Sér. A–B 285(16) (1977), A1103–A1104.Google Scholar
Banach, St. and Tarski, A.. Sur la décomposition des ensembles de points en parties respectivement congruentes. Fund. Math. 6 (1924), 244–277.10.4064/fm-6-1-244-277Google Scholar
Bartholdi, L.. Amenability of groups and G-sets. Sequences, Groups, and Number Theory. Eds. Berthé, V. and Rigo, M.. Springer, Cham, 2018, pp. 433–544.10.1007/978-3-319-69152-7_11Google Scholar
Bartholdi, L. and Erschler, A.. Poisson–Furstenberg boundary and growth of groups. Probab. Theory Related Fields 168(1–2) (2017), 347–372.10.1007/s00440-016-0712-6Google Scholar
Blackwell, D.. On transient Markov processes with a countable number of states and stationary transition probabilities. Ann. Math. Statist. 26(4) (1955), 654–658.Google Scholar
Cannon, J. W., Floyd, W. J. and Parry, W. R.. Introductory notes on Richard Thompson’s groups. Enseign. Math. (2) 42(3–4) (1996), 215–256.Google Scholar
Ceccherini-Silberstein, T., Grigorchuk, R. I. and de la Harpe, P.. Amenability and paradoxical decompositions for pseudogroups and for discrete metric spaces. Tr. Mat. Inst. Steklova 224 (1998), 57–97.Google Scholar
Choquet, G. and Deny, J.. Sur l’équation de convolution 𝜇 =𝜇 ∗𝜎. C. R. Acad. Sci. Paris 250 (1960), 799–801.Google Scholar
Cohen, J. M.. Cogrowth and amenability of discrete groups. J. Funct. Anal. 48(3) (1982), 301–309.Google Scholar
Derriennic, Y.. Quelques applications du théorème ergodique sous-additif. Astérisque 74 (1980), 183–201.Google Scholar
Durrett, R.. Probability: Theory and Examples (Duxbury Advanced Series) . 3rd edn. Brooks/Cole, Belmont, CA, 2005.Google Scholar
Erschler, A.. Poisson–Furstenberg boundaries, large-scale geometry and growth of groups. Proceedings of the International Congress of Mathematicians, Vol. II. Hindustan Book Agency, New Delhi, 2010, pp. 681–704.Google Scholar
Erschler, A.. Poisson–Furstenberg boundary of random walks on wreath products and free metabelian groups. Comment. Math. Helv. 86(1) (2011), 113–143.10.4171/CMH/220Google Scholar
Frisch, J., Hartman, Y., Tamuz, O. and Vahidi Ferdowsi, P.. Choquet–Deny groups and the infinite conjugacy class property. Ann. of Math. (2) 190(1) (2019), 307–320.Google Scholar
Greenleaf, F. P.. Invariant Means on Topological Groups and Their Applications (Van Nostrand Mathematical Studies) . Van Nostrand Reinhold Co., New York, 1969.Google Scholar
Grigorchuk, R. I.. Symmetric random walks on discrete groups. Uspekhi Mat. Nauk 32(6(198)) (1977), 217–218.Google Scholar
Grigorchuk, R. I.. Symmetric random walks on discrete groups. Adv. Probab. Related Topics 6 (1980), 285–325.Google Scholar
Juschenko, K.. A remark on Liouville property of strongly transitive actions. Preprint, 2018, arXiv:1806.02753.Google Scholar
Juschenko, K. and Zheng, T.. Infinitely supported Liouville measures of Schreier graphs. Groups Geom. Dyn. 12 (2018), 911–918.10.4171/GGD/464Google Scholar
Kaimanovich, V. A.. Examples of nonabelian discrete groups with nontrivial exit boundary. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 123 (1983), 167–184.Google Scholar
Kaimanovich, V. A.. The differential entropy of the boundary of a random walk on a group. Russian Math. Surveys 38(5) (1983), 142–143.10.1070/RM1983v038n05ABEH003509Google Scholar
Kaimanovich, V. A.. Poisson boundaries of random walks on discrete solvable groups. Probability Measures on Groups X. Ed. Heyer, H.. Springer US, Boston, MA, 1991, pp. 205–238.10.1007/978-1-4899-2364-6_16Google Scholar
Kaimanovich, V. A.. Poisson boundary of discrete groups. Preprint, 2007, https://pdfs.semanticscholar.org/e57e/101165b91423f5577d21e6ce8b9430f03fab.pdf.Google Scholar
Kaimanovich, V. A.. Thompson’s group F is not Liouville. Groups, Graphs and Random Walks (London Mathematical Society Lecture Note Series) . Eds. Ceccherini-Silberstein, T., Salvatori, M. and Sava-Huss, E.. Cambridge University Press, Cambridge, 2017, pp. 300–342.10.1017/9781316576571.013Google Scholar
Kaimanovich, V. A. and Vershik, A. M.. Random walks on discrete groups: boundary and entropy. Ann. Probab. 11(3) (1983), 457–490.Google Scholar
Kechris, A. S., Pestov, V. G. and Todorcevic, S.. Fraisse limits, Ramsey theory, and topological dynamics of automorphism groups. Geom. Funct. Anal. 15(1) (2003), 106–189.Google Scholar
Kesten, H.. Full Banach mean values on countable groups. Math. Scand. 7 (1959), 146–156.10.7146/math.scand.a-10568Google Scholar
Kim, S.-H., Koberda, T. and Lodha, Y.. Chain groups of homeomorphisms of the interval and the circle. Preprint, 2016, arXiv:1610.04099.Google Scholar
Lodha, Y.. A nonamenable type $F_{\infty }$ group of piecewise projective homeomorphisms. Preprint, 2014, arXiv:1408.3127.Google Scholar
Lodha, Y.. An upper bound for the Tarski numbers of non amenable groups of piecewise projective homeomorphisms. Internat. J. Algebra Comput. 27 (2016), 315–322.10.1142/S0218196717500151Google Scholar
Lodha, Y. and Moore, J. T.. A nonamenable finitely presented group of piecewise projective homeomorphisms. Groups Geom. Dyn. 10(1) (2016), 177–200.10.4171/GGD/347Google Scholar
Meier, J.. Groups, Graphs and Trees. Cambridge University Press, Cambridge, 2008.Google Scholar
Mishchenko, P.. Boundary of the action of Thompson group F on dyadic numbers. Preprint, 2015, arXiv:1512.03083.Google Scholar
Monod, N.. Groups of piecewise projective homeomorphisms. Proc. Natl. Acad. Sci. USA 110(12) (2013), 4524–4527.10.1073/pnas.1218426110Google Scholar
Mordell, L. J.. Diophantine Equations (Pure and Applied Mathematics) . Academic Press, London, 1969.Google Scholar
Neumann, J.. Zur allgemeinen Theorie des Masses. Fundamenta Mathematicae 13(1) (1929), 73–116.10.4064/fm-13-1-73-116Google Scholar
Novikov, P. S. and Adyan, S. I.. On infinite periodic groups. I, II, III. Izv. Akad. Nauk SSSR Ser. Mat. 32 (1968), 212–244, 251–524, 709–731.Google Scholar
Yu Ol’shanskii, A.. An infinite group with subgroups of prime orders. Izv. Akad. Nauk SSSR Ser. Mat. 44(2) (1980), 309–321.Google Scholar
Yu Ol’shanskii, A.. On the question of the existence of an invariant mean on a group. Russian Math. Surveys 35(4) (1980), 180–181.10.1070/RM1980v035n04ABEH001876Google Scholar
Yu Ol’shanskii, A. and Sapir, M. V.. Non-amenable finitely presented torsion-by-cyclic groups. Publ. Math. Inst. Hautes Études Sci. 96(1) (2003), 43–169.10.1007/s10240-002-0006-7Google Scholar
Pestov, V. G.. On free actions, minimal flows, and a problem by Ellis. Trans. Amer. Math. Soc. 350(10) (1998), 4149–4165.Google Scholar
Rosenblatt, J.. Ergodic and mixing random walks on locally compact groups. Math. Ann. 257(1) (1981), 31–42.10.1007/BF01450653Google Scholar
Savchuk, D.. Some graphs related to Thompson’s group F . Combinatorial and Geometric Group Theory. Eds. Bogopolski, O., Bumagin, I., Kharlampovich, O. and Ventura, E.. Birkhäuser Basel, Basel, 2010, pp. 279–296.Google Scholar
Schneider, F. M. and Thom, A.. The Liouville property and random walks on topological groups. Preprint, 2019, arXiv:1902.10243.Google Scholar
Szwarc, R.. A short proof of the Grigorchuk–Cohen cogrowth theorem. Proc. Amer. Math. Soc. 106(3) (1989), 663–665.10.1090/S0002-9939-1989-0975660-2Google Scholar
Tarski, A.. Algebraische Fassung des Massproblems. Fund. Math. 31 (1938), 47–66.10.4064/fm-31-1-207-223Google Scholar
Varopoulos, N. Th.. Brownian motion and transient groups. Ann. Inst. Fourier (Grenoble) 33(2) (1983), 241–261.10.5802/aif.926Google Scholar
Wagon, S.. The Banach–Tarski Paradox (Encyclopedia of Mathematics and its Applications) . Cambridge University Press, Cambridge, 1993.Google Scholar
Woess, W.. Random Walks on Infinite Graphs and Groups (Cambridge Tracts in Mathematics) . Cambridge University Press, Cambridge, 2000.10.1017/CBO9780511470967Google Scholar