Search

We prove Abelian and Tauberian theorems for regularized Cauchy transforms of positive Borel measures on the real line whose distribution functions grow at most polynomially at infinity. In particular, we relate the asymptotics of the distribution functions to the asymptotics of the regularized Cauchy transform.

Assume that for a measurable funcion f on (0, ∞) there exist a positive auxiliary function a(t) and some γ ∈ R such that 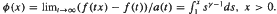. Then f is said to be of generalized regular variation. In order to control the asymptotic behaviour of certain estimators for distributions in extreme value theory we are led to study regular variation of second order, that is, we assume that 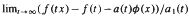exists non-trivially with a second auxiliary function a1(t). We study the possible limit functions in this limit relation (defining generalized regular variation of second order) and their domains of attraction. Furthermore we give the corresponding relation for the inverse function of a monotone f with the stated property. Finally, we present an Abel-Tauber theorem relating these functions and their Laplace transforms.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Karamata's theorem for regularized Cauchy transforms

Generalized regular variation of second order

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Karamata's theorem for regularized Cauchy transforms

Generalized regular variation of second order