Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T17:44:39.603Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized regular variation of second order

Part of: Inversion theorems Real functions

Published online by Cambridge University Press:  09 April 2009

Laurens de Haan  and
Ulrich Stadtmüller
Laurens de Haan
Affiliation:
Erasmus University Econometric Institute P. O. Box 1738 3000 DR Rotterdam The Netherlands
Ulrich Stadtmüller
Affiliation:
Universität Ulm Abt. Math. III 89069 Ulm Germany e-mail: stamue@mathematik.uni-ulm.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

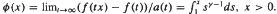Assume that for a measurable funcion f on (0, ∞) there exist a positive auxiliary function a(t) and some γ ∈ R such that . Then f is said to be of generalized regular variation. In order to control the asymptotic behaviour of certain estimators for distributions in extreme value theory we are led to study regular variation of second order, that is, we assume that 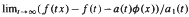exists non-trivially with a second auxiliary function a1(t). We study the possible limit functions in this limit relation (defining generalized regular variation of second order) and their domains of attraction. Furthermore we give the corresponding relation for the inverse function of a monotone f with the stated property. Finally, we present an Abel-Tauber theorem relating these functions and their Laplace transforms.

Keywords

Regular variationSecond order variationlimit functionsdomain of attractioninverse functionsLaplace transformAbelian theoremTauberian theorem

MSC classification

Secondary: 26A12: Rate of growth of functions, orders of infinity, slowly varying functions 40E05: Tauberian theorems, general
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 61 , Issue 3 , December 1996 , pp. 381 - 395
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Bingham, N. H., Goldie, C. M. and Teugels, J. L., Regular variation, Encyclopedia Math. Appl. 27 (Cambridge University Press, Cambridge, 1987).CrossRefGoogle Scholar
[2]Davis, R. and Resnick, S., ‘Tail estimates motivated by extreme value theory’, Ann. Statist. 12 (1984), 1467–1487.CrossRefGoogle Scholar
[3]Dekkers, A. and de Haan, L., ‘On the estimation of the extreme-value index and large quantile estimation’, Ann. Statist. 17 (1989), 1795–1832.CrossRefGoogle Scholar
[4]Dekkers, A. and de Haan, L., ‘Optimal choice of a sample fraction in extreme-value estimation’, J. Multivariate Anal. 47 (1993), 173–195.CrossRefGoogle Scholar
[5]Dekker, A. L. M., On extreme-value estimation (Ph.D. Thesis, Erasmus University, Rotterdam, 1991).Google Scholar
[6]Gawronski, W. and Stadtmüller, U., ‘Parameter estimations for distributions with regularly varying tails’, Statist. Decisions 3 (1985), 297–316.Google Scholar
[7]Geluk, J. L., ‘Π-regular variation, Proc. Amer. Math. Soc. 82 (1981), 565–570.Google Scholar
[8]Geluk, J. L. and de Haan, L., Regular variation, extensions and Tauberian theorems, CWI Tract 40 (CWI, Amsterdam, 1987).Google Scholar
[9]Goldie, C. M. and Smith, R. L., ‘Slow variation with remainder: Theory and applications’, Quart. J. Math. Oxford Ser. 2 38 (1987), 45–71.CrossRefGoogle Scholar
[10]de Haan, L., ‘Equivalence classes of regularly varying functions’, Stochastic Processes Appl. 2 (1974), 243–259.CrossRefGoogle Scholar
[11]de Haan, L. and Resnick, S., ‘Second-order regular variation and rates of convergence in extremevalue theory’, Ann. Probab. 24 (1996), 97–124.Google Scholar
[12]Hall, P., ‘On some estimates of an exponent of regular variation’, J. Roy. Statist. Soc. Ser. B. 44 (1982), 37–42.Google Scholar
[13]Omey, E. and Willekens, E., ‘Π-variation with remainder’, J. London Math. Soc. 37 (1988), 105–118.CrossRefGoogle Scholar
[14]Pereira, T. T., ‘Second order behaviour of domains of attraction and the bias of generalized Pickands' estimator’, in Extreme value theory and applications III (eds. Galambos, J., Lechner, J., Simiu, E.) NIST special publication 886 (1994) pp. 165–177.Google Scholar
[15]Seneta, E., Regularly varying functions, Lecture Notes in Math. 508 (Springer, Berlin, 1976).CrossRefGoogle Scholar
[16]Smith, R. L., ‘Uniform rates of convergence in extreme value theory’, Adv. in Appl. Probab. 14 (1982), 600–622.CrossRefGoogle Scholar
[17]Vervaat, W., ‘Functional CLT's for processes with positive drift and their inverses’, Z. Wahrsch. Verw. Gebiete 23 (1972), 245–253.CrossRefGoogle Scholar