A new class of life distributions, namely new better than used in convex ordering (NBUC), and its dual, new worse than used in convex ordering (NWUC), are introduced. Their relations to other classes of life distributions, closure properties under three reliability operations, and heritage properties under shock model and Laplace-Stieltjes transform are discussed.

A family of random variables {X(θ)} parameterized by the parameter θ satisfies stochastic convexity (SCX) if and only if for any increasing and convex function f(x), Ef[X(θ)] is convex in θ. This definition, however, has a major drawback for the lack of certain important closure properties. In this paper we establish the notion of strong stochastic convexity (SSCX), which implies SCX. We demonstrate that SSCX is a property enjoyed by a wide range of random variables. We also show that SSCX is preserved under random mixture, random summation, and any increasing and convex operations that are applied to a set of independent random variables. These closure properties greatly facilitate the study of parametric convexity of many stochastic systems. Applications to GI/G/1 queues, tandem and cyclic queues, and tree-like networks are discussed. We also demonstrate the application of SSCX in bounding the performance of certain systems.

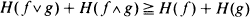Suppose that pulses arrive according to a Poisson process of rate λ with the duration of each pulse independently chosen from a distribution F having finite mean. Let X(t) be the shot noise process formed by the superposition of these pulses. We consider functionals H(X) of the sample path of X(t). H is said to be L-superadditive if for all functions 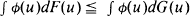f and g. For any distribution F for the pulse durations, we define H(F) = EH(X). We prove that if H is L-superadditive and for all convex functions 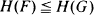ϕ, then . Various consequences of this result are explored.

It is shown that the stationary waiting time random variables W′, W″ of two M/G/l queueing systems for which the corresponding service time random variables satisfy E(S′−x)+ ≦ E(S″−x)+ (all x >0), are stochastically ordered as W′≦dW″. The weaker conclusion, that E(W′−x)+ ≦ E(W″−x)+ (all x > 0), is shown to hold in GI/M/k systems when the interarrival time random variables satisfy E(x−T′)+ ≦ E(x−T″)+ (all x). A sufficient condition for wk≡EW in GI/D/k to be monotonic in k for a sequence of k-server queues with the same relative traffic intensity is given. Evidence indicating or refuting possible strengthenings of some of the results is indicated.