Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Błaszczyszyn, Bartłomiej
and
Yogeshwaran, D.
2009.
Directionally convex ordering of random measures, shot noise fields, and some applications to wireless communications.
Advances in Applied Probability,
Vol. 41,
Issue. 3,
p.
623.
Budhiraja, Amarjit
and
Nyquist, Pierre
2015.
Large deviations for multidimensional state-dependent shot-noise processes.
Journal of Applied Probability,
Vol. 52,
Issue. 4,
p.
1097.
Budhiraja, Amarjit
and
Nyquist, Pierre
2015.
Large deviations for multidimensional state-dependent shot-noise processes.
Journal of Applied Probability,
Vol. 52,
Issue. 04,
p.
1097.
Pang, Guodong
and
Zhou, Yuhang
2018.
Functional limit theorems for a new class of non-stationary shot noise processes.
Stochastic Processes and their Applications,
Vol. 128,
Issue. 2,
p.
505.
Pang, Guodong
and
Taqqu, Murad S.
2019.
Nonstationary self‐similar Gaussian processes as scaling limits of power‐law shot noise processes and generalizations of fractional Brownian motion.
High Frequency,
Vol. 2,
Issue. 2,
p.
95.
Pang, Guodong
and
Zhou, Yuhang
2020.
Functional Limit Theorems for Shot Noise Processes with Weakly Dependent Noises.
Stochastic Systems,
Vol. 10,
Issue. 2,
p.
99.
Anugu, Sumith Reddy
and
Pang, Guodong
2024.
Sample path moderate deviations for shot noise processes in the high intensity regime.
Stochastic Processes and their Applications,
Vol. 176,
Issue. ,
p.
104432.

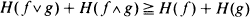 for all functions
for all functions 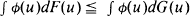 for all convex functions
for all convex functions 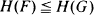 . Various consequences of this result are explored.
. Various consequences of this result are explored.