We study families of rational curves on irreducible holomorphic symplectic varieties. We give a necessary and sufficient condition for a sufficiently ample linear system on a holomorphic symplectic variety of $K3^{[n]}$-type to contain a uniruled divisor covered by rational curves of primitive class. In particular, for any fixed $n$, we show that there are only finitely many polarization types of holomorphic symplectic variety of $K3^{[n]}$-type that do not contain such a uniruled divisor. As an application, we provide a generalization of a result due to Beauville–Voisin on the Chow group of $0$-cycles on such varieties.

We study the Chow ring of the moduli stack 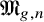$\mathfrak {M}_{g,n}$ of prestable curves and define the notion of tautological classes on this stack. We extend formulas for intersection products and functoriality of tautological classes under natural morphisms from the case of the tautological ring of the moduli space 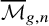$\overline {\mathcal {M}}_{g,n}$ of stable curves. This paper provides foundations for the paper [BS21].

In the appendix (jointly with J. Skowera), we develop the theory of a proper, but not necessary projective, pushforward of algebraic cycles. The proper pushforward is necessary for the construction of the tautological rings of 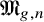$\mathfrak {M}_{g,n}$ and is important in its own right. We also develop operational Chow groups for algebraic stacks.

In this paper, we prove a decomposition result for the Chow groups of projectivizations of coherent sheaves of homological dimension $\le 1$ . In this process, we establish the decomposition of Chow groups for the cases of the Cayley trick and standard flips. Moreover, we apply these results to study the Chow groups of symmetric powers of curves, nested Hilbert schemes of surfaces, and the varieties resolving Voisin maps for cubic fourfolds.

In this article we introduce the local versions of the Voevodsky category of motives with $\mathbb{F} _p$ -coefficients over a field k, parametrized by finitely generated extensions of k. We introduce the so-called flexible fields, passage to which is conservative on motives. We demonstrate that, over flexible fields, the constructed local motivic categories are much simpler than the global one and more reminiscent of a topological counterpart. This provides handy ‘local’ invariants from which one can read motivic information. We compute the local motivic cohomology of a point for $p=2$ and study the local Chow motivic category. We introduce local Chow groups and conjecture that over flexible fields these should coincide with Chow groups modulo numerical equivalence with $\mathbb{F} _p$ -coefficients, which implies that local Chow motives coincide with numerical Chow motives. We prove this conjecture in various cases.

The Beauville–Voisin conjecture for a hyperkähler manifold $X$ states that the subring of the Chow ring $A^{\ast }(X)$ generated by divisor classes and Chern characters of the tangent bundle injects into the cohomology ring of $X$. We prove a weak version of this conjecture when $X$ is the Hilbert scheme of points on a K3 surface for the subring generated by divisor classes and tautological classes. This in particular implies the weak splitting conjecture of Beauville for these geometries. In the process, we extend Lehn’s formula and the Li–Qin–Wang $W_{1+\infty }$ algebra action from cohomology to Chow groups for the Hilbert scheme of an arbitrary smooth projective surface $S$.

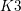Moduli spaces of stable objects in the derived category of a $K3$ surface provide a large class of holomorphic symplectic varieties. In this paper, we study the interplay between Chern classes of stable objects and zero-cycles on holomorphic symplectic varieties which arise as moduli spaces. First, we show that the second Chern class of any object in the derived category lies in a suitable piece of O’Grady’s filtration on the $\text{CH}_{0}$-group of the $K3$ surface. This solves a conjecture of O’Grady and improves on previous results of Huybrechts, O’Grady, and Voisin. Second, we propose a candidate for the Beauville–Voisin filtration on the $\text{CH}_{0}$-group of the moduli space of stable objects. We discuss its connection with Voisin’s recent proposal via constant cycle subvarieties, and prove a conjecture of hers on the existence of special algebraically coisotropic subvarieties for the moduli space.

Given a smooth variety $X$ and an effective Cartier divisor $D\subset X$, we show that the cohomological Chow group of 0-cycles on the double of $X$ along $D$ has a canonical decomposition in terms of the Chow group of 0-cycles $\text{CH}_{0}(X)$ and the Chow group of 0-cycles with modulus $\text{CH}_{0}(X|D)$ on $X$. When $X$ is projective, we construct an Albanese variety with modulus and show that this is the universal regular quotient of $\text{CH}_{0}(X|D)$. As a consequence of the above decomposition, we prove the Roitman torsion theorem for the 0-cycles with modulus. We show that $\text{CH}_{0}(X|D)$ is torsion-free and there is an injective cycle class map $\text{CH}_{0}(X|D){\hookrightarrow}K_{0}(X,D)$ if $X$ is affine. For a smooth affine surface $X$, this is strengthened to show that $K_{0}(X,D)$ is an extension of $\text{CH}_{1}(X|D)$ by $\text{CH}_{0}(X|D)$.

We formulate a conjectural hard Lefschetz property for Chow groups and prove it in some special cases, roughly speaking, for varieties with finite-dimensional motive, and for varieties whose self-product has vanishing middle-dimensional Griõths group. An appendix includes related statements that follow from results of Vial.

We introduce a Milnor type K-group associated to commutative algebraic groups over a perfect field. It is an additive variant of Somekawa's K-group. We show that the K-group associated to the additive group and q multiplicative groups of a field is isomorphic to the space of absolute Kähler differentials of degree q of the field, thus giving us a geometric interpretation of the space of absolute Kähler differentials. We also show that the K-group associated to the additive group and Jacobian variety of a curve is isomorphic to the homology group of a certain complex.

We give a new construction of a weak form of Steenrod operations for Chow groups modulo a prime number p for a certain class of varieties. This class contains projective homogeneous varieties which are either split or considered over a field admitting some form of resolution of singularities, for example any field of characteristic not p. These reduced Steenrod operations are sufficient for some applications to the theory of quadratic forms.

Let X be the variety obtained by the Weil transfer with respect to a quadratic separable field extension of a generalized Severi–Brauer variety. We study (and, in some cases, determine) the canonical dimension, incompressibility, and motivic indecomposability of X. We determine the canonical 2-dimension of X (in the general case).

We compute the Chow group of 0-cycles on a rational surface defined over a finite extension K of the field $\mathbb{Q}_p$ of p-adic numbers (p a prime) when it is split by an unramified extension of K. We use intersection theory to define a specialisation map so we need to assume that the surface admits a regular proper integral model. A family of examples is worked out to illustrate the method.

In this paper, we show that the Chern classes ck of the de Rham bundle ${\cal H}_{{\rm d}R}$ defined on any ‘good’ toroidal compactification $\bar{\cal A}_g$ of the moduli space of Abelian varieties of dimension g are zero in the rational Chow ring of $\bar{\cal A}_g$, for g = 4, 5 and k>0.

We investigate the Chow groups of zero cycles of products of curves over a p-adic field by means of the Milnor K-groups of their Jacobians as introduced by Somekawa. We prove some finiteness results for CH0(X)/m for X a product of curves over a p-adic field.

J. Murre has conjectured that every smooth projective variety X of dimension d admits a decomposition of the diagonal δ=p$_0$+…+p$_2d$ ∈ CH$^d$(X × X) [otimes] Q such that the cycles p$_i$ are orthogonal projectors which lift the Künneth components of the identity map in étale cohomology. If this decomposition induces an intrinsic filtration on the Chow groups of X, we call it a Murre decomposition. In this paper we propose candidates for such projectors on 3-folds by using fiber structures. Using Mori theory, we prove that every smooth uniruled complex 3-fold admits a Murre decomposition.

We study here the O-dimension Chow group of some particular smooth varieties which are fibrations over curves (i.e. are equipped with a proper, surjective morphism over a smooth curve). We obtain finiteness results for fibrations, whose generic fibres are Severi-Brauer varieties of squarefree index, when the group field is a number field (or in some particular cases a finitely generated field over Q).