Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T20:28:37.803Z Has data issue: false hasContentIssue false
  • English
  • Français

LEHN’S FORMULA IN CHOW AND CONJECTURES OF BEAUVILLE AND VOISIN

Part of: Cycles and subschemes

Published online by Cambridge University Press:  30 July 2020

Davesh Maulik  and
Andrei Neguţ Open the ORCID record for Andrei Neguţ [Opens in a new window]
Davesh Maulik
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, 77 Massachusetts Avenue, Cambridge, MA02139, USA (maulik@mit.edu)
Andrei Neguţ
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, 77 Massachusetts Avenue, Cambridge, MA02139, USA (maulik@mit.edu) Simion Stoilow Institute of Mathematics, Bucharest, Romania (andrei.negut@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

The Beauville–Voisin conjecture for a hyperkähler manifold 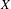$X$ states that the subring of the Chow ring 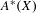$A^{\ast }(X)$ generated by divisor classes and Chern characters of the tangent bundle injects into the cohomology ring of 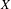$X$. We prove a weak version of this conjecture when 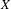$X$ is the Hilbert scheme of points on a K3 surface for the subring generated by divisor classes and tautological classes. This in particular implies the weak splitting conjecture of Beauville for these geometries. In the process, we extend Lehn’s formula and the Li–Qin–Wang 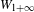$W_{1+\infty }$ algebra action from cohomology to Chow groups for the Hilbert scheme of an arbitrary smooth projective surface $S$.

Keywords

Algebraic cyclesBeauville-Voisin conjectureChow groupsHilbert schemesVirasoro algebra

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes) 14C15: (Equivariant) Chow groups and rings; motives 14C25: Algebraic cycles
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 933 - 971
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beauville, A., Varietes Kähleriennes dont la premiere classe de Chern est nulle, J. Differential Geom. 18 (1983), 755–782.Google Scholar
Beauville, A., On the splitting of the Bloch–Beilinson filtration, in Algebraic Cycles and Motives, London Mathematical Society Lecture Notes, Volume 344 (Cambridge University Press, Cambridge, 2007).Google Scholar
Beauville, A. and Voisin, C., On the Chow ring of a K3 surface, J. Algebraic Geom. 13 (2004), 417–426.CrossRefGoogle Scholar
de Cataldo, M. and Migliorini, L., The Chow groups and the motive of the Hilbert scheme of points on a surface, J. Algebra 251(2) (2002), 824–848.CrossRefGoogle Scholar
Feigin, B. L. and Fuchs, D. B., Verma modules over a Virasoro algebra, Funktsional. Anal. i Prilozhen. 17(3) (1983), 91–92.Google Scholar
Fogarty, J., Algebraic families on an algebraic surface, II, the Picard scheme of the punctual Hilbert scheme, Amer. J. Math. 95(3) (1973), 660–687.CrossRefGoogle Scholar
Fu, L. and Tian, Z., Motivic hyperkähler resolution conjecture II: Hilbert schemes of K3 surfaces, http://math.univ-lyon1.fr/fu/articles/MotivicCrepantHilbK3.pdf.Google Scholar
Fulton, W., Intersection Theory (Springer, New York, 1998). ISBN 978-1-4612-1700-8.CrossRefGoogle Scholar
Grojnowski, I., Instantons and affine algebras I. The Hilbert scheme and vertex operators, Math. Res. Lett. 3(2) (1996), 275–291.CrossRefGoogle Scholar
Kimura, S.-I., Chow groups are finite dimensional, in some sense, Math. Ann. 331(1) (2005), 173–201.CrossRefGoogle Scholar
Lehn, M., Chern classes of tautological sheaves on Hilbert schemes of points on surfaces, Invent. Math. 136(1) (1999), 157–207.CrossRefGoogle Scholar
Li, W.-P., Qin, Z. and Wang, W., Hilbert schemes and W-algebras, Int. Math. Res. Not. 2002(27) (2002), 1427–1456.CrossRefGoogle Scholar
Nakajima, H., Heisenberg algebra and Hilbert schemes of points on projective surfaces, Ann. Math. 145(2) (1997), 379–388.CrossRefGoogle Scholar
Nakajima, H., Lectures on Hilbert Schemes of Points on Surfaces, University Lecture Series, Volume 18, pp. xii+132 (American Mathematical Society, Providence, RI, 1999). ISBN: 0-8218-1956-9.Google Scholar
Neguţ, A., Shuffle algebras associated to surfaces, Sel. Math. New Ser. 25 36 (2019). doi:10.1007/s00029-019-0481-z.Google Scholar
Neguţ, A., $W$ -algebras associated to surfaces, preprint, 2017, arXiv:1710.03217.Google Scholar
Neguţ, A., Hecke correspondences for smooth moduli spaces of sheaves, preprint, 2018, arXiv:1804.03645.Google Scholar
Voisin, C., On the Chow ring of certain algebraic hyper-Kähler manifolds, Pure Appl. Math. Q. (4) 3(2) (2008), 613–649.CrossRefGoogle Scholar
Yin, Q., Finite-dimensionality and cycles on powers of K3 surfaces, Comment. Math. Helv. 90 (2015), 503–511.CrossRefGoogle Scholar