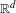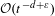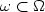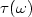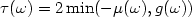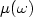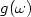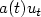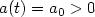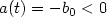We improve a previous result about the local energy decay for the damped wave equation on $\mathbb{R}^{d}$. The problem is governed by a Laplacian associated with a long-range perturbation of the flat metric and a short-range absorption index. Our purpose is to recover the decay ${\mathcal{O}}(t^{-d+\unicode[STIX]{x1D700}})$ in the weighted energy spaces. The proof is based on uniform resolvent estimates, given by an improved version of the dissipative Mourre theory. In particular, we have to prove the limiting absorption principle for the powers of the resolvent with inserted weights.

The energy in a square membrane Ω subject to constant viscous dampingon a subset $\omega\subset \Omega$ decays exponentially in timeas soon as ωsatisfies a geometrical condition known as the “Bardos-Lebeau-Rauch” condition. The rate $\tau(\omega)$ of this decay satisfies $\tau(\omega)= 2 \min( -\mu(\omega),g(\omega))$ (see Lebeau [Math.Phys. Stud.19 (1996) 73–109]). Here $\mu(\omega)$ denotes the spectral abscissa of thedamped wave equation operator and  $g(\omega)$ is a number called the geometrical quantity of ω and defined as follows.A ray in Ω is the trajectory generated by thefree motion of a mass-point in Ω subject to elastic reflections on theboundary. These reflections obey the law of geometrical optics.The geometrical quantity $g(\omega)$ is then defined as the upper limit (large timeasymptotics) of the average trajectory length. We give here an algorithm to compute explicitly $g(\omega)$ when ωis a finite union of squares.

In this paper we elaborate a model to describe some aspects of the human lung considered as a continuous, deformable, medium. To that purpose, westudy the asymptotic behavior of aspring-mass system with dissipation. The key feature of our approach is the nature of this dissipation phenomena, which is related here to the flow of a viscous fluid through a dyadic tree of pipes (the branches), each exit of which being connected to an air pocket (alvelola) delimited by two successive masses.The first part focuses on the relation between fluxes and pressures at the outlets of a dyadic tree, assuming the flow within the tree obeys Poiseuille-like laws. In a second part, which contains the main convergence result, we intertwine the outlets of the tree with a spring-mass array. Letting again the number of generations (and therefore the number of masses) go to infinity, we show that the solutions to the finite dimensional problems converge in a weak sense to the solution of a wave-like partial differential equation with a non-local dissipative term.

We consider the planar random motion of a particle that moves with constant finite speed c and, at Poisson-distributed times, changes its direction θ with uniform law in [0, 2π). This model represents the natural two-dimensional counterpart of the well-known Goldstein–Kac telegraph process. For the particle's position (X(t), Y(t)), t > 0, we obtain the explicit conditional distribution when the number of changes of direction is fixed. From this, we derive the explicit probability law f(x, y, t) of (X(t), Y(t)) and show that the density p(x, y, t) of its absolutely continuous component is the fundamental solution to the planar wave equation with damping. We also show that, under the usual Kac condition on the velocity c and the intensity λ of the Poisson process, the density p tends to the transition density of planar Brownian motion. Some discussions concerning the probabilistic structure of wave diffusion with damping are presented and some applications of the model are sketched.

The Green's function for the damped wave equation on a finite interval subject to two Robin boundary conditions is studied. The problem for a semi-infinite interval with one Robin boundary is considered first by the Laplace transform method to establish the reflection principle at a Robin boundary. It is seen that the reflected wave generated by an exiting wave at a Robin boundary is a convolution involving the exiting wave and some kernel function. This generalizes the well known classical results for reflections at Dirichlet and Neumann boundaries. The reflection principle at a Robin boundary is then used for the finite interval case by considering multiple reflections and this leads to an infinite sequence of waves. In order to justify the results obtained here we also study the finite interval case by the Laplace transform method. The Laplace transform of the Green's function is expanded, for large values of the transform parameter, into an infinite series of negative exponentials and then inverted term by term. Agreement is reached between these two approaches.

Motivated by several works on the stabilization of the oscillator by on-off feedbacks, we study the related problem for the one-dimensional wave equation, damped by an on-off feedback $a(t)u_t$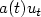. We obtain results that are radically different from those known in the case of the oscillator. We consider periodic functions a: typically a is equal to 1 on (0,T), equal to 0 on (T, qT) and is qT-periodic. We study the boundary case and next the locally distributed case, and we give optimal results of stability. In both cases, we prove that there are explicit exceptional values of T for which the energy of some solutions remains constant with time. If T is different from those exceptional values, the energy of all solutions decays exponentially to zero. This number of exceptional values is countable in the boundary case and finite in the distributed case. 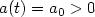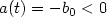When the feedback is acting on the boundary, we also study the case of postive-negative feedbacks: $a(t) = a_0 >0$ on (0,T), and $a(t) = -b_0 <0 $ on (T,qT), and we give the necessary and sufficient condition under which the energy (that is no more nonincreasing with time) goes to zero or goes to infinity. The proofs of these results are based on congruence properties and on a theorem of Weyl in the boundary case, and on new observability inequalities for the undamped wave equation, weakening the usual “optimal time condition” in the locally distributed case. These new inequalities provide also new exact controllability results.