We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a simple method to estimate the number of distinct copies of some classes of spanning subgraphs in hypergraphs with a high minimum degree. In particular, for each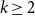 
$k\geq 2$ and 
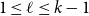$1\leq \ell \leq k-1$, we show that every 
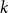$k$-graph on 
$n$ vertices with minimum codegree at leastcontains 
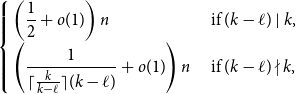\begin{equation*} \left \{\begin {array}{l@{\quad}l} \left (\dfrac {1}{2}+o(1)\right )n & \text { if }(k-\ell )\mid k,\\[5pt] \left (\dfrac {1}{\lceil \frac {k}{k-\ell }\rceil (k-\ell )}+o(1)\right )n & \text { if }(k-\ell )\nmid k, \end {array} \right . \end{equation*}
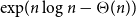$\exp\!(n\log n-\Theta (n))$ Hamilton 
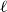$\ell$-cycles as long as 
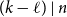$(k-\ell )\mid n$. When 
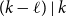$(k-\ell )\mid k$, this gives a simple proof of a result of Glock, Gould, Joos, Kühn, and Osthus, while when 
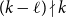$(k-\ell )\nmid k$, this gives a weaker count than that given by Ferber, Hardiman, and Mond, or when 
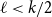$\ell \lt k/2$, by Ferber, Krivelevich, and Sudakov, but one that holds for an asymptotically optimal minimum codegree bound.
We show that for every 
$n\in \mathbb N$ and 
$\log n\le d\lt n$, if a graph 
$G$ has 
$N=\Theta (dn)$ vertices and minimum degree 
$(1+o(1))\frac{N}{2}$, then it contains a spanning subdivision of every 
$n$-vertex 
$d$-regular graph.
