We study the number of ways of factoring elements in the complex reflection groups
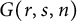 $G(r,s,n)$
as products of reflections. We prove a result that compares factorization numbers in
$G(r,s,n)$
as products of reflections. We prove a result that compares factorization numbers in
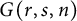 $G(r,s,n)$
to those in the symmetric group
$G(r,s,n)$
to those in the symmetric group
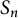 $S_n$
, and we use this comparison, along with the Ekedahl, Lando, Shapiro, and Vainshtein (ELSV) formula, to deduce a polynomial structure for factorizations in
$S_n$
, and we use this comparison, along with the Ekedahl, Lando, Shapiro, and Vainshtein (ELSV) formula, to deduce a polynomial structure for factorizations in
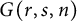 $G(r,s,n)$
.
$G(r,s,n)$
.