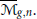Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cavalieri, Renzo
2016.
Hurwitz theory and the double ramification cycle.
Japanese Journal of Mathematics,
Vol. 11,
Issue. 2,
p.
305.
Cavalieri, Renzo
Markwig, Hannah
and
Ranganathan, Dhruv
2023.
Tropical and Logarithmic Methods in Enumerative Geometry.
Vol. 52,
Issue. ,
p.
85.
Cavalieri, Renzo
Markwig, Hannah
and
Ranganathan, Dhruv
2023.
Tropical and Logarithmic Methods in Enumerative Geometry.
Vol. 52,
Issue. ,
p.
73.
Cavalieri, Renzo
Markwig, Hannah
and
Ranganathan, Dhruv
2024.
Pluricanonical cycles and tropical covers.
Transactions of the American Mathematical Society,
Corey, Daniel
Markwig, Hannah
and
Ranganathan, Dhruv
2025.
Counting Tropical Curves in ℙ1 × ℙ1 : Computation and Polynomiality Properties.
International Mathematics Research Notices,
Vol. 2025,
Issue. 15,
Cavalieri, Renzo
Markwig, Hannah
and
Schmitt, Johannes
2025.
k-leaky double Hurwitz descendants.
Forum of Mathematics, Sigma,
Vol. 13,
Issue. ,