We consider Weiss's and Downton's models with parametersπ, αand β depending on i number of susceptibles and j number of carriers. A martingale argument is performed when πand α /β only depend on i or, in Weiss's case, when α /β is the product of a function of i by a function of j. In these cases the martingale approach proves very valuable and gives explicit results quite easily. In particular it shows that well-known relations between moments and integrals along a trajectory are still true for any stopping time and for more general models than the classic ones.

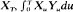The purpose of this paper is to give some very simple applications of martingales to epidemics. The results are all connected with stopping times T (for instance the classical end of epidemic) and include the expression of the joint generating function Laplace transform of and 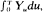and simple relations between moments of these three variables. (Here Xt and Yt respectively denote the numbers of susceptibles and carriers.) We also give several relations between different types of epidemics. Although this paper only deals with Downton's model, some of the methods are still valid for more general models.