Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Picard, Philippe
1981.
Applications of martingale theory to carrier-borne epidemic models with time-dependent parameters.
Mathematical Biosciences,
Vol. 55,
Issue. 3-4,
p.
205.
Demongeot, Jacques
1983.
Transactions of the Ninth Prague Conference.
p.
183.
Picard, Philippe
1984.
Applications of martingale theory to some epidemic models, II.
Journal of Applied Probability,
Vol. 21,
Issue. 04,
p.
677.
Lemoine, Austin J.
1987.
On sojourn time in Jackson networks of queues.
Journal of Applied Probability,
Vol. 24,
Issue. 02,
p.
495.
Biswas, S.
and
Noor, Hamed Saad
1989.
A Note on the Application of Martingales in a Problem of Non‐Communicable Epidemics.
Biometrical Journal,
Vol. 31,
Issue. 4,
p.
487.
Ball, Frank
1990.
Stochastic Processes in Epidemic Theory.
Vol. 86,
Issue. ,
p.
71.
Ball, Frank
1990.
A note on the total size distribution of carrier-borne epidemic models.
Journal of Applied Probability,
Vol. 27,
Issue. 04,
p.
908.
Lefevre, Claude
and
Picard, Philippe
1990.
A non-standard family of polynomials and the final size distribution of Reed-Frost epidemic processes.
Advances in Applied Probability,
Vol. 22,
Issue. 1,
p.
25.
Lefèvre, Claude
1990.
Stochastic Processes in Epidemic Theory.
Vol. 86,
Issue. ,
p.
1.
Picard, Philippe
and
Lefevre, Claude
1990.
A unified analysis of the final size and severity distribution in collective Reed-Frost epidemic processes.
Advances in Applied Probability,
Vol. 22,
Issue. 02,
p.
269.
Pi card, Philippe
and
Lefévre, Claude
1991.
Another look at ganl's carrier-borne epidemic model with two stages of infection.
Communications in Statistics. Stochastic Models,
Vol. 7,
Issue. 1,
p.
107.
Biswas, S.
and
Thomas, M.
1992.
On a Martingale Approach for the Estimation of the Parameters of a Bivariate Carrier Borne Epidemic Model in Presence of a Linear Relationship Between Carriers and Suspectibles.
Biometrical Journal,
Vol. 34,
Issue. 2,
p.
219.
Picard, Philippe
and
Lefèvre, Claude
1993.
Distribution of the final state and severity of epidemics with fatal risk.
Stochastic Processes and their Applications,
Vol. 48,
Issue. 2,
p.
277.
Parthasarathy, P. R.
and
Kumar, B. Krishna
1993.
Density‐dependent birth and death processes with immigration.
International Journal of Mathematical Education in Science and Technology,
Vol. 24,
Issue. 1,
p.
55.
Picard, Philippe
and
Lefèvre, Claude
1996.
First crossing of basic counting processes with lower non-linear boundaries: A unified approach through pseudopolynomials (I).
Advances in Applied Probability,
Vol. 28,
Issue. 03,
p.
853.
Lefèvre, Claude
and
Picard, Philippe
1996.
Abelian-type expansions and non-linear death processes(II).
Advances in Applied Probability,
Vol. 28,
Issue. 3,
p.
877.
Picard, Philippe
1998.
A semi-hybrid model for malaria with limited superinfection.
Advances in Applied Probability,
Vol. 30,
Issue. 4,
p.
1027.
Picard, Philippe
and
Lefèvre, Claude
1999.
On the algebraic structure in Markovian processes of death and epidemic types.
Advances in Applied Probability,
Vol. 31,
Issue. 03,
p.
742.
Clancy, Damian
1999.
Outcomes of epidemic models with general infection and removal rate functions at certain stopping times.
Journal of Applied Probability,
Vol. 36,
Issue. 3,
p.
799.
Clancy, Damian
1999.
Outcomes of epidemic models with general infection and removal rate functions at certain stopping times.
Journal of Applied Probability,
Vol. 36,
Issue. 03,
p.
799.

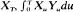 and
and 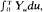 and simple relations between moments of these three variables. (Here
and simple relations between moments of these three variables. (Here 