1 results
Steady-State Response to Periodic Excitation in Fractional Vibration System
-
- Journal:
- Journal of Mechanics / Volume 32 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 04 January 2016, pp. 25-33
- Print publication:
- February 2016
-
- Article
- Export citation
-
The steady-state response to periodic excitation in the linear fractional vibration system was considered by using the fractional derivative operator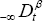
. First we investigated the response to the harmonic excitation in the form of complex exponential function. The amplitude-frequency relation and phase-frequency relation were derived. The effect of the fractional derivative term on the stiffness and damping was discussed. For the case of periodic excitation, we decompose the periodic excitation into a superposition of harmonic excitations by using the Fourier series, and then utilize the results for harmonic excitations and the principle of superposition, where our adopted tactics avoid appearing a fractional power of negative numbers to overcome the difficulty in fractional case. Finally we demonstrate the proposed method by three numerical examples.
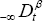. First we investigated the response to the harmonic excitation in the form of complex exponential function. The amplitude-frequency relation and phase-frequency relation were derived. The effect of the fractional derivative term on the stiffness and damping was discussed. For the case of periodic excitation, we decompose the periodic excitation into a superposition of harmonic excitations by using the Fourier series, and then utilize the results for harmonic excitations and the principle of superposition, where our adopted tactics avoid appearing a fractional power of negative numbers to overcome the difficulty in fractional case. Finally we demonstrate the proposed method by three numerical examples.