Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T08:12:40.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady-State Response to Periodic Excitation in Fractional Vibration System

Published online by Cambridge University Press:  04 January 2016

C. Huang  and
J.-S. Duan
C. Huang
Affiliation:
School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai, China
J.-S. Duan*
Affiliation:
School of Sciences, Shanghai Institute of Technology, Shanghai, China
*
* (duanjs@sit.edu.cn)
Get access

Abstract

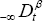The steady-state response to periodic excitation in the linear fractional vibration system was considered by using the fractional derivative operator . First we investigated the response to the harmonic excitation in the form of complex exponential function. The amplitude-frequency relation and phase-frequency relation were derived. The effect of the fractional derivative term on the stiffness and damping was discussed. For the case of periodic excitation, we decompose the periodic excitation into a superposition of harmonic excitations by using the Fourier series, and then utilize the results for harmonic excitations and the principle of superposition, where our adopted tactics avoid appearing a fractional power of negative numbers to overcome the difficulty in fractional case. Finally we demonstrate the proposed method by three numerical examples.

Keywords

Fractional calculusFractional vibrationResponseExcitation.
Type
Research Article
Information
Journal of Mechanics , Volume 32 , Issue 1 , February 2016 , pp. 25 - 33
Copyright
Copyright © The Society of Theoretical and Applied Mechanics, R.O.C. 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Podlubny, I., Fractional Differential Equations, Academic, San Diego (1999).Google Scholar
2.Kilbas, A. A., Srivastava, H. M. and Trujillo, J. J., Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam (2006).Google Scholar
3.Mainardi, F., Fractional Calculus and Waves in Linear Viscoelasticity, Imperial College, London (2010).Google Scholar
4.Băleanu, D., Diethelm, K., Scalas, E. and Trujillo, J. J., Fractional Calculus Models and Numerical Methods, Series on Complexity, Nonlinearity and Chaos, World Scientific, Boston (2012).Google Scholar
5.Machado, J. T., Kiryakova, V. and Mainardi, F., “Recent History of Fractional Calculus,” Communications in Nonlinear Science and Numerical Simulation, 16, pp. 1140–1153 (2011).Google Scholar
6.Rossikhin, Y. A. and Shitikova, M. V., “Applications of Fractional Calculus to Dynamic Problems of Linear and Nonlinear Hereditary Mechanisms of Solids,” Applied Mechanics Reviews, 50, pp. 15–67 (1997).Google Scholar
7.Scott-Blair, G. W., “The Role of Psychophysics in Rheology,” Journal of Colloid Science, 2, pp. 21–32 (1947).Google Scholar
8.Gerasimov, A. N., “A Generalization of Linear Laws of Deformation and Its Application to Inner Friction Problems,” Prikladnaya Matematikai Mekhanika, 12, pp. 251–259 (1948).Google Scholar
9.Koeller, R. C., “Applications of Fractional Calculus to the Theory of Viscoelasticity,” Journal of Applied Mechanics, 51, pp. 299–307 (1984).Google Scholar
10.Xu, M. Y. and Tan, W. C., “Representation of the Constitutive Equation of Viscoelastic Materials by the Generalized Fractional Element Networks and Its Generalized Solutions,” Science in China Series G, 46, pp. 145–157 (2003).Google Scholar
11.Chen, W., “An Intuitive Study of Fractional Derivative Modeling and Fractional Quantum in Soft Matter,” Journal of Vibration and Control, 14, pp. 1651–1657 (2008).Google Scholar
12.Caputo, M., “Linear Models of Dissipation Whose Q is Almost Frequency Independent, Part II,” Geophysical Journal Royal Astronomical Society, 13, pp. 529–539 (1967).Google Scholar
13.Scott-Blair, G. W., “Analytical and Integrative Aspects of the Stress-Strain-Time Problem,” Journal of Scientific Instruments, 21, pp. 80–84 (1944).Google Scholar
14.Scott-Blair, G. W., A Survey of General and Applied Rheology, Pitman, London (1949).Google Scholar
15.Bland, D. R., The Theory of Linear Viscoelasticity, Pergamon, Oxford (1960).Google Scholar
16.Bagley, R. L. and Torvik, P. J., “A Generalized Derivative Model for an Elastomer Damper,” Shock and Vibration Bulletin, 49, pp. 135–143 (1979).Google Scholar
17.Beyer, H. and Kempfle, S., “Definition of Physically Consistent Damping Laws with Fractional Derivatives,” ZAMM, Journal of Applied Mathematics and Mechanics, 75, pp. 623–635 (1995).CrossRefGoogle Scholar
18.Gorenflo, R. and Mainardi, F., “Fractional Calculus: Integral and Differential Equations of Fractional Order,” in: Carpinteri, A. and Mainardi, F. (Eds.), Fractals and Fractional Calculus in Continuum Mechanics, Springer-Verlag, Wien/New York, pp. 223–276 (1997).Google Scholar
19.Achar, B. N. N., Hanneken, J. W. and Clarke, T., “Response Characteristics of a Fractional Oscillator,” Physica A, 309, pp. 275–288 (2002).Google Scholar
20.Li, M., Lim, S. C. and Chen, S., “Exact Solution of Impulse Response to a Class of Fractional Oscillators and Its Stability,” Mathematical Problems in Engineering, 2011, Article ID 657839 (2011).CrossRefGoogle Scholar
21.Lim, S. C., Li, M. and Teo, L. P., “Locally Self-Similar Fractional Oscillator Processess,” Fluctuation and Noise Letters, 7, pp. L169–L179 (2007).Google Scholar
22.Lim, S. C. and Teo, L. P., “The Fractional Oscillator Process with Two Indices,” Journal of Physics A: Mathematical and Theoretical, 42, Article ID 065208 (2009).Google Scholar
23.Shen, Y. J., Yang, S. P. and Xing, H. J., “Dynamical Analysis of Linear Single Degree-of-Freedom Oscillator with Fractional-Order Derivative,” Acta Physica Sinica, 61, 110505-1-6 (2012).Google Scholar
24.Shen, Y., Yang, S., Xing, H. and Gao, G., “Primary Resonance of Duffing Oscillator with Fractional-Order Derivative,” Communications in Nonlinear Science and Numerical Simulation, 17, pp. 3092–3100 (2012).Google Scholar
25.Li, C. P., Deng, W. H. and Xu, D., “Chaos Synchronization of the Chua System with a Fractional Order,” Physica A, 360, pp. 171–185 (2006).Google Scholar
26.Zhang, W., Liao, S. K. and Shimizu, N., “Dynamic Behaviors of Nonlinear Fractional-Order Differential Oscillator,” Journal of Mechanical Science and Technology, 23, pp. 1058–1064 (2009).Google Scholar
27.Wang, Z. H. and Hu, H. Y., “Stability of a Linear Oscillator with Damping Force of the Fractional-Order Derivative,” Science in China Series G, 53, pp. 345–352 (2010).Google Scholar
28.Li, C. and Ma, Y., “Fractional Dynamical System and Its Linearization Theorem,” Nonlinear Dynamics, 71, pp. 621–633 (2013).Google Scholar
29.Kaslik, E. and Sivasundaram, S., “Non-Existence of Periodic Solutions in Fractional-Order Dynamical Systems and a Remarkable Difference Between Integer and Fractional-Order Derivatives of Periodic Functions,” Nonlinear Analysis: Real World Applications, 13, pp. 1489–1497 (2012).Google Scholar
30.Duan, J. S., Wang, Z., Liu, Y. L. and Qiu, X., “Eigenvalue Problems for Fractional Ordinary Differential Equations,” Chaos, Solitons & Fractals, 46, pp. 46–53 (2013).Google Scholar
31.Agarwal, R. P., Andrade, B. D. and Cuevas, C., “Weighted Pseudo-Almost Periodic Solutions of a Class of Semilinear Fractional Differential Equations,” Nonlinear Analysis: Real World Applications, 11, pp. 3532–3554 (2010).Google Scholar