1 results
Ruin probabilities via local adjustment coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 736-755
- Print publication:
- September 1995
-
- Article
- Export citation
-
Let ψ(u) be the ruin probability in a risk process with initial reserve u, Poisson arrival rate β, claim size distribution B and premium rate p(x) at level x of the reserve. Let y(x) be the non-zero solution of the local Lundberg equation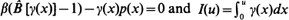
. It is shown that 
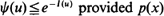is non-decreasing and that log ψ(u) ≈ –I(u) in a slow Markov walk limit. Though the results and conditions are of large deviations type, the proofs are elementary and utilize piecewise comparisons with standard risk processes with a constant p. Also simulation via importance sampling using local exponential change of measure defined in terms of the γ(x) is discussed and some numerical results are presented.
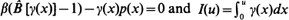. It is shown that 
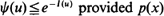is non-decreasing and that log ψ(u) ≈ –