Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T22:05:48.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Ruin probabilities via local adjustment coefficients

Part of: Probabilistic methods, simulation and stochastic differential equations Special processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Søren Asmussen  and
Hanne Mandrup Nielsen
Søren Asmussen*
Affiliation:
Aalborg University
Hanne Mandrup Nielsen*
Affiliation:
Baltica Insurance Company, Copenhagen
*
∗Postal address: Institute of Electronic Systems, Aalborg University, Fr. Bajersv. 7E, DK 9220 Aalborg, Denmark.
∗∗Postal address: Baltica Insurance Company, Copenhagen, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let ψ(u) be the ruin probability in a risk process with initial reserve u, Poisson arrival rate β, claim size distribution B and premium rate p(x) at level x of the reserve. Let y(x) be the non-zero solution of the local Lundberg equation 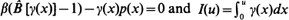. It is shown that 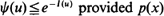is non-decreasing and that log ψ(u) ≈ –I(u) in a slow Markov walk limit. Though the results and conditions are of large deviations type, the proofs are elementary and utilize piecewise comparisons with standard risk processes with a constant p. Also simulation via importance sampling using local exponential change of measure defined in terms of the γ(x) is discussed and some numerical results are presented.

Keywords

FAST SIMULATIONLARGE DEVIATIONSLUNDBERG INEQUALITYMARTINGALERARE EVENTSSLOW MARKOV WALKSTORAGE PROCESS

MSC classification

Primary: 60F10: Large deviations
Secondary: 60K30: Applications (congestion, allocation, storage, traffic, etc.) 65C05: Monte Carlo methods
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 3 , September 1995 , pp. 736 - 755
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Asmussen, S. (1987) Applied Probability and Queues. Wiley, Chichester.Google Scholar
[2] Asmussen, S. (1982) Conditioned limit theorems relating a random walk to its associate, with applications to risk reserve processes and the GI/G/1 queue. Adv. Appl. Prob. 14, 143–170.CrossRefGoogle Scholar
[3] Asmussen, S. (1985) Conjugate processes and the simulation of ruin problems. Stoch, Proc. Appl. 20, 213–229.CrossRefGoogle Scholar
[4] Asmussen, S. (1995) Ruin Probabilities. World Scientific, Singapore.Google Scholar
[5] Asmussen, S. and Schock Petersen, S. (1989) Ruin probabilities expressed in terms of storage processes. Adv. Appl. Prob. 20, 913–916.CrossRefGoogle Scholar
[6] Asmussen, S. and Rolski, T. (1991) Computational methods in risk theory: a matrix-algorithmic approach. Insurance: Math Econom. 10, 259–274.Google Scholar
[7] Asmussen, S. and Rubinstein, R. Y. (1995) Complexity properties of steady-state rare events simulation in queueing models. Frontiers in Queueing, ed. Dshalalow, J. CRC Press, Boca Raton.Google Scholar
[8] Bucklew, J. A. (1990) Large Deviation Techniques in Decision, Simulation and Estimation. Wiley, New York.Google Scholar
[9] Cottrell, M., Fort, J.-C. and Malgouyres, G. (1983) Large deviations and rare events in the study of stochastic algorithms. IEEE Trans. Autom. Control 28, 907–920.CrossRefGoogle Scholar
[10] Dassion, A. and Embrechts, P. (1989) Martingales and insurance risk. Stoch. Models 5, 181–217.Google Scholar
[11] Djehiche, B. (1993) A large deviation estimate for ruin probabilities. Scand. Actuarial J. 42–59.CrossRefGoogle Scholar
[12] Dynkin, E. B. (1965) Markov Processes I. Springer-Verlag, Berlin.Google Scholar
[13] Embrechts, P., Grandell, J. and Schmidli, H. (1993) Finite-time Lundberg inequalities in the Cox case. Scand. Actuarial J. 17–41.CrossRefGoogle Scholar
[14] Fleming, W. H. and Rishel, R. W. (1975) Deterministic and Stochastic Optimal Control. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[15] Grandell, J. (1990) Aspects of Risk Theory. Springer-Verlag, Berlin.Google Scholar
[16] Grandell, J. (1992) Finite time ruin probabilities and martingales. Informatica 2, 3–32.Google Scholar
[17] Heidelberger, P. (1993) Fast simulation of rare events in queueing and reliability theory. IBM Research Report RC 19028, Yorktown Heights, New York. Preliminary version published in Performance Evaluation of Computer and Communications Systems, Springer Lecture Notes in Computer Science 729, 165–202.Google Scholar
[18] Karlin, S. and Taylor, H. M. (1981) A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
[19] Küchler, U. and S⊘rensen, M. (1993) Exponential families of Markov processes. Manuscript, Aarhus University.Google Scholar
[20] Kunita, H. (1976) Absolute continuity of Markov processes. Seminaire de Probabilités X. Lecture Notes in Mathematics 511, 44–77. Springer-Verlag, Berlin.Google Scholar
[21] Lehtonen, T and Nyrhinen, H. (1992) Simulating level-crossing probabilities by importance sampling. Adv. Appl. Prob. 24, 858–874.CrossRefGoogle Scholar
[22] Martin-Löf, A. (1983) Entropy estimates for ruin probabilities. In Probability and Mathematical Statistics, ed. Gut, A. and Holst, J., pp. 29–39.Google Scholar
[23] Martin-Löf, A. (1986) Entropy, a useful concept in risk theory. Scand. Actuarial J. 223–235.CrossRefGoogle Scholar
[24] Meyn, S. P. and Tweedie, R. L. (1993) Markov Chains and Stochastic Stability. Springer-Verlag, New York.CrossRefGoogle Scholar
[25] Neuts, M. F. (1981) Matrix-Geometric Solutions in Stochastic Models. Johns Hopkins University Press, Baltimore.Google Scholar
[26] Nielsen, H. M. (1994) Generalization of Lundberg Conjugation to Processes with Premiums Depending on the Reserve. Cand. act. dissertation (in Danish). Laboratory of Insurance Mathematics, University of Copenhagen.Google Scholar
[27] Siegmund, D. (1976) Importance sampling in the Monte Carlo study of sequential tests. Ann. Statist. 4, 914–924.CrossRefGoogle Scholar
[28] Taylor, G. C. (1980) Probability of ruin with variable premium rate. Scand. Actuarial J. 57–76.CrossRefGoogle Scholar