Let 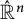$\hat {\mathbb {R}}^n$ be the one-point compactification of 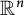$\mathbb {R}^n$ obtained by adding a point at infinity. We say that a subset 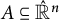$A\subseteq \hat {\mathbb {R}}^n$ is 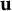$\mathbf {u}$-convex if for every pair of points 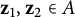$\mathbf {z}_1, \mathbf {z}_2 \in A$, the arc of the unique circle through 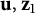$\mathbf {u}, \mathbf {z}_1$ and 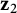$\mathbf {z}_2$, from 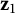$\mathbf {z}_1$ to 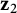$\mathbf {z}_2$ and not containing 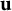$\mathbf {u}$, is contained in A. In this case, we call 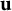$\mathbf {u}$ a pole of A. When the pole 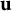$\mathbf {u}$ approaches infinity, 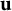$\mathbf {u}$-convex sets become convex in the classical sense.

The notion of polar convexity in the complex plane has been used to analyze the behavior of critical points of polynomials. In this paper, we extend the notion to finite-dimensional Euclidean spaces. The goal of this paper is to start building the theory of polar convexity and to show that the introduction of a pole creates a richer theory. For example, polar convexity enjoys a beautiful duality (see Theorem 4.3) that does not exist in classical convexity. We formulate polar analogues of several classical results of the alternatives, such as Gordan’s and Farkas’ lemmas; see Section 5. Finally, we give a full description of the convex hull of finitely many points with respect to finitely many poles; see Theorem 6.7.

We discuss the reconciliation problem between probability measures: given n⩾2 probability spaces $(\Omega,{\mathcal{F}}_1,{\mathbb{P}}_1),\ldots,(\Omega,{\mathcal{F}}_n,{\mathbb{P}}_n)$ with a common sample space, does there exist an overall probability measure ${\mathbb{P}} \ \text{on} \ {\mathcal{F}} = \sigma({\mathcal{F}}_1,\ldots,{\mathcal{F}}_n)$ such that, for all i, the restriction of ${\mathbb{P}} \ \text{to} \ {\mathcal{F}}_i$ coincides with ${\mathbb{P}}_i$? General criteria for the existence of a reconciliation are stated, along with some counterexamples that highlight some delicate issues. Connections to earlier (recent and far less recent) work are discussed, and elementary self-contained proofs for the various results are given.