No CrossRef data available.
Article contents
Reconciliation of probability measures
Part of:
Foundations of probability theory
Published online by Cambridge University Press: 17 December 2018
Abstract
We discuss the reconciliation problem between probability measures: given n⩾2 probability spaces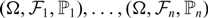 
$(\Omega,{\mathcal{F}}_1,{\mathbb{P}}_1),\ldots,(\Omega,{\mathcal{F}}_n,{\mathbb{P}}_n)$ with a common sample space, does there exist an overall probability measure 
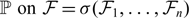${\mathbb{P}} \ \text{on} \ {\mathcal{F}} = \sigma({\mathcal{F}}_1,\ldots,{\mathcal{F}}_n)$ such that, for all i, the restriction of 
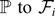${\mathbb{P}} \ \text{to} \ {\mathcal{F}}_i$ coincides with 
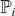${\mathbb{P}}_i$? General criteria for the existence of a reconciliation are stated, along with some counterexamples that highlight some delicate issues. Connections to earlier (recent and far less recent) work are discussed, and elementary self-contained proofs for the various results are given.
MSC classification
- Type
- Papers
- Information
- European Journal of Applied Mathematics , Volume 30 , Special Issue 6: Applied Optimal Transport , December 2019 , pp. 1300 - 1310
- Copyright
- © Cambridge University Press 2018
References
Alon, S. & Lehrer, E. (2014) Subjective multi-prior probability: a representation of a partial likelihood relation. J. Econ. Theory 151, 476–492.CrossRefGoogle Scholar
Bertrand, J. & Puel, M. (2013) The optimal mass transport problem for relativistic costs. Calc. Var. Partial Differ. Equ. 46(1–2), 353–374.CrossRefGoogle Scholar
Billingsley, P. (1999) Convergence of Probability Measures, 2nd ed., Wiley Series in Probability and Statistics: Probability and Statistics, John Wiley & Sons Inc., New York. A Wiley-Interscience Publication.CrossRefGoogle Scholar
Cambou, M. & Filipović, D. (2017) Model uncertainty and scenario aggregation. Math. Finance 27(2), 534–567.CrossRefGoogle Scholar
Dall’Aglio, G. (1961) Sulle distribuzioni doppie con margini assegnati sogette a delle limitazioni. G. Ist. Ital. Attuari 24, 94–108.Google Scholar
Dall’Aglio, G., Kotz, S. & Salinetti, G. (editors) (1991) Advances in Probability Distributions with Given Marginals, Mathematics and Its Applications, Vol. 67, Kluwer Academic Publishers Group, Dordrecht. Beyond the copulas, Papers from the Symposium on Distributions with Given Marginals held in Rome, April 1990.Google Scholar
Fréchet, M. (1957) Les tableaux de corrélation dont les marges et des bornes sont données. Ann. Univ. Lyon. Sect. A (3) 20, 13–31.Google Scholar
Jimenez, C. & Santambrogio, F. (2012) Optimal transportation for a quadratic cost with convex constraints and applications. J. Math. Pures Appl. (9) 98(1), 103–113.CrossRefGoogle Scholar
Kellerer, H. (1964) Maßtheoretische Marginalprobleme. Math. Ann. 153, 168–198.CrossRefGoogle Scholar
Kellerer, H. G. (1961) Funktionen auf Produkträumen mit vorgegebenen Marginal-Funktionen. Math. Ann. 144, 323–344.CrossRefGoogle Scholar
Korman, J., McCann, R. J. & Seis, C. (2015) An elementary approach to linear programming duality with application to capacity constrained transport. J. Convex Anal. 22(3), 797–808.Google Scholar
Korman, J., McCann, R. J. & Seis, C. (2015) Dual potentials for capacity constrained optimal transport. Calc. Var. Partial Differ. Equ. 54(1), 573–584.CrossRefGoogle Scholar
Levin, V. L. (1984) The problem of mass transfer in a topological space and probability measures with given marginal measures on the product of two spaces. Dokl. Akad. Nauk SSSR 276(5), 1059–1064.Google Scholar
Strassen, V. (1965) The existence of probability measures with given marginals. Ann. Math. Stat. 36, 423–439.CrossRefGoogle Scholar