Since Faltings proved Mordell’s conjecture in [16] in 1983, we have known that the sets of rational points on curves of genus at least 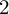$2$ are finite. Determining these sets in individual cases is still an unsolved problem. Chabauty’s method (1941) [10] is to intersect, for a prime number p, in the p-adic Lie group of p-adic points of the Jacobian, the closure of the Mordell–Weil group with the p-adic points of the curve. Under the condition that the Mordell–Weil rank is less than the genus, Chabauty’s method, in combination with other methods such as the Mordell–Weil sieve, has been applied successfully to determine all rational points in many cases.

Minhyong Kim’s nonabelian Chabauty programme aims to remove the condition on the rank. The simplest case, called quadratic Chabauty, was developed by Balakrishnan, Besser, Dogra, Müller, Tuitman and Vonk, and applied in a tour de force to the so-called cursed curve (rank and genus both 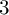$3$ ).

This article aims to make the quadratic Chabauty method small and geometric again, by describing it in terms of only ‘simple algebraic geometry’ (line bundles over the Jacobian and models over the integers).

The number of insecticide applications made by an apple grower to control an insect infestation is modeled as a geometric random variable. Insecticide efficacy, rate per application, month of treatment, and method of application all have significant impacts on the expected number of applications. The number of applications to control a given insect population is dependent on the probability of achieving successful control with a given application. Results suggest that northeastern growers have the highest and mid-Atlantic growers the lowest probability of controlling an infestation with a given application. Results also indicate that scales require the least and moths the most number of applications. Growers are not responsive to per unit insecticide prices, but respond negatively to insecticide toxicity, supporting findings from previous pesticide demand analyses.

This paper gives an overview of recurrence and ergodicity properties of a Markov chain. Two new notions for ergodicity and recurrence are introduced. They are called μ -geometric ergodicity and μ -geometric recurrence respectively. The first condition generalises geometric as well as strong ergodicity. Our key theorem shows that μ -geometric ergodicity is equivalent to weak μ -geometric recurrence. The latter condition is verified for the time-discretised two-centre open Jackson network. Hence, the corresponding two-dimensional Markov chain is μ -geometrically and geometrically ergodic, but not strongly ergodic. A consequence of μ -geometric ergodicity with μ of product-form is the convergence of the Laplace-Stieltjes transforms of the marginal distributions. Consequently all moments converge.

A class of multivariate exponential distributions is suggested which includes those presented by Marshall and Olkin, Downton, and Hawkes. It is based on a concept of hierarchical successive damage. Recursive expressions for the Laplace transforms and for first and second moments are derived in the bivariate case. Related multivariate geometric distributions are described.