1 results
The Craighero–Gattazzo surface is simply connected
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 28 February 2017, pp. 557-585
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
-
We show that the Craighero–Gattazzo surface, the minimal resolution of an explicit complex quintic surface with four elliptic singularities, is simply connected. This was conjectured by Dolgachev and Werner, who proved that its fundamental group has a trivial profinite completion. The Craighero–Gattazzo surface is the only explicit example of a smooth simply connected complex surface of geometric genus zero with ample canonical class. We hope that our method will find other applications: to prove a topological fact about a complex surface we use an algebraic reduction mod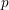
$p$ technique and deformation theory.
