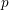Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Franciosi, Marco
Pardini, Rita
and
Rollenske, Sönke
2018.
Gorenstein stable Godeaux surfaces.
Selecta Mathematica,
Vol. 24,
Issue. 4,
p.
3349.
İnanç Baykur, R.
2022.
Small exotic 4-manifolds and symplectic
Calabi–Yau surfaces via genus-3 pencils.
Open Book Series,
Vol. 5,
Issue. 1,
p.
185.
Reyes, Javier
and
Urzúa, Giancarlo
2022.
Rational configurations in K3 surfaces and simply-connected $$p_g=1$$ surfaces with $$K^2=1,2,3,4,5,6,7,8,9$$.
Mathematische Zeitschrift,
Vol. 302,
Issue. 4,
p.
2435.
Lehmann, Brian
Sengupta, Akash Kumar
and
Tanimoto, Sho
2022.
Geometric consistency of Manin's conjecture.
Compositio Mathematica,
Vol. 158,
Issue. 6,
p.
1375.