We study generalised quasirandom graphs whose vertex set consists of $q$ parts (of not necessarily the same sizes) with edges within each part and between each pair of parts distributed quasirandomly; such graphs correspond to the stochastic block model studied in statistics and network science. Lovász and Sós showed that the structure of such graphs is forced by homomorphism densities of graphs with at most $(10q)^q+q$ vertices; subsequently, Lovász refined the argument to show that graphs with $4(2q+3)^8$ vertices suffice. Our results imply that the structure of generalised quasirandom graphs with $q\ge 2$ parts is forced by homomorphism densities of graphs with at most $4q^2-q$ vertices, and, if vertices in distinct parts have distinct degrees, then $2q+1$ vertices suffice. The latter improves the bound of $8q-4$ due to Spencer.

We introduce and study analogues of expander and hyperfinite graph sequences in the context of directed acyclic graphs, which we call ‘extender’ and ‘hypershallow’ graph sequences, respectively. Our main result is a probabilistic construction of non-hypershallow graph sequences.

We present a new approach to graph limit theory that unifies and generalizes the two most well-developed directions, namely dense graph limits (even the more general 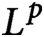$L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form 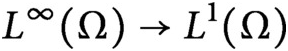$L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces 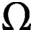$\Omega $ . We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. 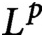Graphons, $L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.