Article contents
Action convergence of operators and graphs
Published online by Cambridge University Press: 17 September 2020
Abstract
We present a new approach to graph limit theory that unifies and generalizes the two most well-developed directions, namely dense graph limits (even the more general 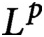 $L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form
$L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form 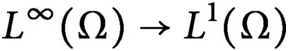 $L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces
$L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces 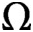 $\Omega $. We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. Graphons,
$\Omega $. We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. Graphons, 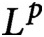 $L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.
$L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement n°617747. The research was partially supported by the MTA Rényi Institute Lendület Limits of Structures Research Group, and partially by the Mathematical Foundations of Artificial Intelligence project of the National Excellence Programme (grant no. 2018-1.2.1-NKP-2018-00008). A. B. was supported by the “Bolyai Ösztöndíj” of the Hungarian Academy of Sciences.
References
- 27
- Cited by


