In the absence of oxygen, Fe(II) chloride, sulfate, and carbonate solutions react at pH 6.5 to 7 with aluminum hydroxide suspensions to form new Fe(II)-Al(III) hydroxy anion compounds of the pyroaurite group. The Fe(II)-Al(III) hydroxy-chloride and -sulfate compounds are isostructural with Fe(II)- Fe(III) “green rust” compounds with A1 essentially substituting for Fe(III). Where CO32- is the only anion in the system, an Fe(II)-Al(III) compound isostructural with hydrotalcite is formed. Either in the dried or wet state, these compounds are unstable in air due to oxidation of Fe(II). Oxidation of the dried sample in air yields akaganeite or aluminous ferrihydrite, whereas, if the sample is maintained in a moist condition and oxidized by air under water, lepidocrocite or aluminous goethite is produced along with small amounts of ferrihydrite. On X-ray powder diffraction, the lepidocrocite so formed commonly shows no diagnostic (020) basal reflection, or one with a markedly reduced intensity. The products of oxidation, and the rapidity of their formation, appear to be dependent on the composition of the initial double hydroxy compound and the conditions under which the oxidation is carried out.

The green colored compounds commonly observed in gleyed soils also rapidly become yellow brown on exposure to air, and difficulty arises in the identification of the Fe oxide phases assumed to be present. Similar conditions and reactants to those involved in the formation of the compounds described above are expected in these soils, and it is suggested that Fe(II)-Al(III) members of the pyroaurite group may form in such an environment.

The formation of fine-grained magnetite (~0.1 μm) at pH 7 and 25°C from aeration of Fe(II) chloride solutions is presented. The magnetite converted at 105°C to maghemite with poorly developed superstructure lines. Under the experimental conditions employed, as the initial [Cl]/[Fe] ratio was increased from the stoichiometric value of 2, the final product contained increasing amounts of lepidocrocite. The degree of crystallinity of this phase, as measured by the width at half height of the 020 X-ray diffraction peak, also increased with this ratio. The hydrolysis rate (base consumption to maintain pH) showed a plateau whose position and extent changed with the initial [Cl]/[Fe] ratio. Through this plateau region the Eh decreased to a minimum value the position of which was directly related to the [Cl]/[Fe] value. The formation of lepidocrocite rather than magnetite is likely due to the high [Cl] where there would be increased difficulty for neighboring OH to condense and eliminate H2O. The formation of Fe-O-Fe bonds in this condensation would be impeded by Cl substitution for OH either in the first formed green rust stage or during its oxidation.

Diffractograms of lepidocrocites formed from the oxidation of Fe(II) chloride solutions at pH 7 and 25°C showed differential line broadening with (0k0) reflections being much sharper than (hk0) or (hkl). As the initial [Cl]/[Fe] ratio was increased from 2, crystallinity increased in all axial directions, as defined by the width at half height of diffraction peaks. At [Cl]/[Fe] ratios greater than ~8, the crystallinity did not increase further, and for reflections involving the a-axis direction, it appeared to decrease. Increased [Cl]/[Fe] ratios changed the rate of the oxidation/hydrolysis reactions. These variations reflect changes in the stability and/or composition of the intermediate green rust phase, (Fe(II)Fe(III) hydroxychloride) in the high [Cl] environment. The influence of the [Cl]/[Fe] ratio was related to the experimental conditions employed, especially where they influenced the rate of oxidation.

Because layered Fe(II)Fe(III)-hydroxides (Green rusts, GRs) are anion exchangers, they represent potential orthophosphate sorbents in anoxic soils and sediments. To evaluate this possibility, two types of experiments with synthetic sulphate-interlayered GRs (GRSO4 = Fe2+4Fe3+2(OH)12SO4 ×H2O) were studied. First, sorption of phosphate in GRSO4 was followed by reacting suspensions of pure GRSO4 synthesized by oxidation of Fe(II) with an excess of Na2HPO4 (pH 9.3). Second the possible incorporation of phosphate in GR during formation by Fe(II)-induced reductive dissolution of phosphate-containing ferrihydrites was examined in systems containing an excess of Fe(II) (pH 7). With excess phosphate in solution, GRSO4 initially sorbed phosphate in the interlayer producing a basal layer spacing of 1.04 nm, but only ~50% of the interlayer sulphate was exchanged with phosphate. This GR slowly transformed to vivianite within months. In the Fe(II)-rich systems, reaction with synthetic ferrihydrites produced GRSO4 similar to that produced by air oxidation. Reaction of Fe(II) with phosphate-containing ferrihydrites initially produced amorphous greenish phosphate containing precipitates which, after 3–4 h, crystallized to GRSO4 and vivianite. In these solutions, stable phosphate-free GRSO4 can form since precipitation of vivianite produced low phosphate activity. Consequently, in both systems GR or amorphous greenish precipitates act as reactive intermediates, but vivianite is the stable end-product limiting phosphate concentration in solution. It is also inferred that Fe(OH)2 is an unlikely phosphate sorbent in mixed Fe(II)-Fe(III) systems because GR phases are more stable (less soluble) than Fe(OH)2.

Fougerite (IMA 2003-057) was accepted by the Commission on New Minerals and Mineral Names of the International Mineralogical Association (IMA) in 2004 as a new mineral to represent the green rust (GR) family. The data on which it was approved, however, are inconsistent. X-ray diffraction patterns from the Fougères soils contain no peaks that could meaningfully be attributed to a GR phase. The sequential dissolution procedure used to identify GR in the soils was not rigorously tested for selectivity. If indeed it is selective, the results indicate the presence of 40–78% Fe in minerals other than GR. Other Fe-bearing phases were not included in the interpretation of the spectroscopy data that were presented. The data are consistent with the presence of Fe-bearing clays and other silicate minerals. In light of the ambiguous and conflicting data, we recommend that the case for fougerite as a mineral be re-evaluated by the IMA.

Fougerite (IMA 2003-057) is a mixed M(II)-M(III) hydroxysalt of the green rust group, where M(II) can be Fe or Mg, and M(III) is Fe. The general structural formula is: ${[{\text{Fe}}_{1-}^{2+}x{\text{Fe}}_x^{3+}{\text{Mg}}_y{(\text{OH})}_{2+2y}]}^{+x}{[x\text{/}n{A}^{-n}.m{\text{H}}_2\text{O}]}^{-x}$ where A is the interlayer anion and n its valency, with 1/4 ≼ x/(1+y) ≼ 1/3 and m ≼ (1−x+y). The structure of green rusts and parent minerals can accommodate a variety of anions, such as OH−, Cl−, ${\text{CO}}_3^{2-},{\text{SO}}_4^{2-}$${\rm{CO}}_3^{2 - },\;{\rm{SO}}_4^{2 - }$. The structure of the mineral was studied by Mössbauer, Raman and X-ray absorption spectroscopies (XAS) at the FeK edge. Mössbauer spectra of the mineral obtained at 78 K are best fitted with four doublets: D1 and D2 due to Fe2+ (isomer shift δ ≈ 1.27 and 1.25 mm s−1, quadrupole splitting ΔEQ ≈ 2.86 and 2.48 mm s−1, respectively) and D3 and D4 due to Fe3+ (δ ≈ 0.46 mm s−1, ΔEQ ≈ 0.48 and 0.97 mm s−1, respectively). Microprobe Raman spectra obtained with a laser at 514.53 nm show the characteristic bands of synthetic green rusts at 427 and 518 cm−1. X-ray absorption spectroscopy shows that Mg is present in the mineral in addition to Fe, that the space group is and the lattice parameter a ≈ 0.30–0.32 nm. The mineral forms by partial oxidation and hydrolysis of aqueous Fe2+, to give small crystals (400–500 nm) in the form of hexagonal plates. The mineral is unstable in air and transforms to lepidocrocite or goethite. The name is for the locality of the occurrence, a forested Gleysol near Fougères, Brittany, France. Its characteristic blue-green color (5BG6/1 in the Munsell system) has long been used as a universal criterion in soil classification to identify Gleysols. From a thermodynamic model of soil-solution equilibria, it was proposed that for the eponymous mineral, Fougères-fougerite, OH− may be the interlayer anion. In other environments, the interlayer anion may be different, and other varieties of fougerite may exist. Fougerite plays a key role in the pathways of formation of Fe oxides.

Mixed FeIIFeIII hydroxides, commonly referred to as ‘green rusts’ (GRs), are important reactive phases in both man-made and natural geochemical systems. Determinations of the standard Gibbs energy of formation of GRs are needed to understand and predict the occurrence and possible reactions of GRs in these systems. Slow acid titration of crystalline green rust sulfate (${\text{GR}}_{{\text{SO}}_4}$\$\end{document}) with the formation of magnetite was used as a novel method to determine the standard Gibbs energy of formation of ${\text{GR}}_{{\text{SO}}_4}$\$\end{document}, ${\text{Δ}}_{\text{f}}{G}^{\text{o}}\left({\text{GR}}_{{\text{SO}}_4}\right)$\$\end{document}. Aqueous suspensions of ${\text{GR}}_{{\text{SO}}_4}$\$\end{document}, with pH slightly >8, were titrated slowly with 1 M H2SO4 until pH = 3 under strict anoxic conditions. Powder X-ray diffraction and Mössbauer analysis revealed that magnetite was the only solid phase formed during the initial part of the titration, where the equilibrium pH was maintained above 7.0. The ratio of Fe2+ release to consumption of protons confirmed the stoichiometry of dissolution of ${\text{GR}}_{{\text{SO}}_4}$\$\end{document} and the formation of magnetite at equilibrium conditions. The estimate of the absolute value of ${\text{Δ}}_{\text{f}}{G}^{\text{o}}\left({\text{GR}}_{{\text{SO}}_4}\right)$\$\end{document} was −3819.43±6.44 kJ mol−1 + y × [ΔfGo(H2O(1))], where y is the number of interlayer water molecules per formula unit. The logarithm of the solubility product, log Ksp, was estimated to be −139.2±4.8 and is invariable with y. Using the new value for ${\text{Δ}}_{\text{f}}{G}^{\text{o}}\left({\text{GR}}_{{\text{SO}}_4}\right)$\$\end{document}, the reduction potentials of several ${\text{GR}}_{{\text{SO}}_4}$\$\end{document}-Fe oxide couples were evaluated, with the ${\text{GR}}_{{\text{SO}}_4}$\$\end{document}-magnetite half cell showing the smallest redox potential at pH 7 and free ion activities of 10−3.

Fe(II)–Fe(III) green rust identified in soil as a natural mineral is responsible for the blue-green color of gley horizons, and exerts the main control on Fe dynamics. A previous EXAFS study of the structure of the mineral confirmed that the mineral belongs to the group of green rusts (GR), but showed that there is a partial substitution of Fe(II) by Mg(II), which leads to the general formula of the mineral: ${[{\text{Fe}}_{1-x}^{2+}{\text{Fe}}_x^{3+}{\text{Mg}}_y{(\text{OH})}_{2+2y}]}^{x+}{[x{\text{OH}}^{-}\cdot m{\text{H}}_2\text{O}]}^{x-}$${[{\rm{Fe}}_{1 - x}^{2 + }{\rm{Fe}}_x^{3 + }{\rm{M}}{{\rm{g}}_y}{({\rm{OH}})_{2 + 2y}}]^{x + }}{[x{\rm{O}}{{\rm{H}}^ - } \cdot m{{\rm{H}}_2}{\rm{O}}]^{x - }}$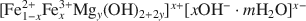. The regular binary solid-solution model proposed previously must be extended to ternary, with provision for incorporation of Mg in the mineral. Assuming ideal substitution between Mg(II) and Fe(II), the chemical potential of any Fe(II)-Fe(III)-Mg(II) hydroxy-hydroxide is obtained as: $\text{μ}=X_1{\text{μ}}_{\text{1}}^{\text{o}}+X_2{\text{μ}}_{\text{2}}^{\text{o}}+X_3{\text{μ}}_{\text{3}}^{\text{o}}+\text{R}T[X_1\text{ln}{X}_1+X_2\text{ln}{X}_2+X_3\text{ln}{X}_3]+A_{12}{X}_2(1-X_2)$${\rm{\mu }} = {X_1}{\rm{\mu }}_{\rm{1}}^{\rm{o}} + {X_2}{\rm{\mu }}_{\rm{2}}^{\rm{o}} + {X_3}{\rm{\mu }}_{\rm{3}}^{\rm{o}} + {\rm{R}}T[{X_1}{\rm{ln}}{X_1} + {X_2}{\rm{ln}}{X_2} + {X_3}{\rm{ln}}{X_3}] + {A_{12}}{X_2}(1 - {X_2})$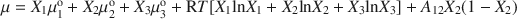. All experimental data show that the mole ratio X2 = Fe(III)/[Fetotal + Mg] is constrained (1) structurally and (2) geochemically. Structurally, Fe(III) ions cannot neighbor each other, which leads to the inequality $X_2\alpha \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right..$${X_2}\leqslant {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 3$}}.$ 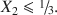Geochemically, Fe(III) cannot be too remote from each other for GR to form as Fe(OH)2 and Mg(OH)2 are very soluble, so $X_2\alpha \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$${X_2}\geqslant {\raise0.5ex\hbox{$\scriptstyle 1$}\kern-0.1em/\kern-0.15em\lower0.25ex\hbox{$\scriptstyle 4$}}$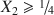. A linear relationship is obtained between the Gibbs free energy of formation of GR, normalized to one Fe atom, and the electronegativity ϰ of the interlayer anion, as: μo/n = −76.887ϰ — 491.5206 (r2 = 0.9985, N = 4), from which the chemical potential of the mineral fougerite μ is obtained in the limiting case X3 = 0, and knowing ${\text{μ}}_{\text{1}}^{\text{o}}=-489.8$${\rm{\mu }}_{\rm{1}}^{\rm{o}} = - 489.8$ 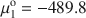kJmol−1 for Fe(OH)2, and ${\text{μ}}_{\text{3}}^{\text{o}}=-832.16$${\rm{\mu }}_{\rm{3}}^{\rm{o}} = - 832.16$ 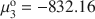kJmol−1 for Mg(OH)2, the two unknown thermodynamic parameters of the solid-solution model are determined as

${\text{μ}}_{\text{2}}^{\text{o}}=+119.18{\text{kJmol}}^{-1}$${\rm{\mu }}_{\rm{2}}^{\rm{o}} = + 119.18\;{\rm{kJmo}}{{\rm{l}}^{ - 1}}$ for Fe(OH)3 (virtual), and A12 = −1456.28 kJmol−1 (non-ideality parameter). From Mössbauer in situ measurements and our model, the chemical composition of the GR mineral is constrained into a narrow range and the soil solutions-mineral equilibria computed. Soil solutions appear to be largely overstaurated with respect to the two forms observed.

Green rusts, GRs, can act as both sorbents and reductants towards selected pollutants. Organo-GRs are expected to combine these properties with a high affinity for hydrophobic substances. A novel organo-GR, GRLAS, was synthesized by incorporating a mixture of linear alkylbenzenesulphonates (LAS) into the interlayer space of synthetic sulphate green rust, GRSO4 . Mössbauer analysis of GRLAS indicates that the structure of the organo-GR is very similar to that of the initial GRSO4 with regard to the FeII/FeIII ratio and local coordination of Fe atoms. X-ray diffraction demonstrates that the GRLAS formed was well ordered, although a mixture of surfactant was used for intercalation. The basal spacings of the GRLAS and the kinetics of the ion-exchange process were dependent on the initial surfactant loading; basal spacings of ~2.85 nm were obtained at LAS solution concentrations >10 mM. The ratio LASadsorbed/SO42–desorbed significantly exceeded the stoichiometric ratio of 2 during the initial part of the ion-exchange process (t = 5 h). However, this ratio was reached progressively with time. GRSO4 preferentially sorbed LAS homologues with long alkyl chains over short ones. Carbon tetrachloride was successfully adsorbed into GRLAS. The adsorption isotherm was linear with a distribution coefficient, Kd, of 505±19 litre kg–1.

In this study, direct evidence for the formation of magnetite via a green rust intermediate is reported. The Fe(II) induced transformation of ferrihydrite, was quantified in situ and under O2-free conditions using synchrotron-based time-resolved energy dispersive X-ray diffraction. At pH 9 and Fe(II)/Fe(III) ratios of 0.5 and 1, rapid growth (6 min) of sulphate green rust and its subsequent transformation to magnetite was observed. Electron microscopy confirmed these results, showing the initial rapid formation of hexagonal sulphate green rust particles, followed by the corrosion of the green rust as magnetite growth occurred, indicating that the reaction proceeds via a dissolution-reprecipitation mechanism. At pH 7 and Fe(II)/Fe(III) ratio of 0.5, sulphate green rust was the stable phase, with no transformation to magnetite.

‘Green rusts’ are a group of reduced Fe hydroxides with a pyroaurite-like structure. In a new occurrence, green rust is present as a 45–60 mm thick band which lies just below the surface (∼4 mm) of an ochreous deposit at an abandoned coal mine site. The sample is characterized by the presence of μm-sized hexagonal crystals which have been identified from SEM imaging. Chemical analyses reveal an Fe(II):Fe(III) ratio which is close to the characteristic 2:1 ratio, and XRD analysis identifies the material by characteristic lattice spacings. The green rust layer also contains aragonite which is not present in the surrounding ochre. Green rusts are important as they have the potential to be used in water treatment.