1 results
Jonsson-like partition relations and j: V → V
-
- Journal:
- The Journal of Symbolic Logic / Volume 69 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1267-1281
- Print publication:
- December 2004
-
- Article
- Export citation
-
Working in the theory ”ZF + There is a nontrivial elementary embedding j : V → V“, we show that a final segment of cardinals satisfies certain square bracket finite and infinite exponent partition relations. As a corollary to this, we show that this final segment is composed of Jonsson cardinals. We then show how to force and bring this situation down to small alephs. A prototypical result is the construction of a model for ZF in which every cardinal μ ≥ ℵ2 satisfies the square bracket infinite exponent partition relation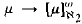
. We conclude with a discussion of some consistency questions concerning different versions of the axiom asserting the existence of a nontrivial elementary embedding j: V → V. By virtue of Kunen's celebrated inconsistency result, we use only a restricted amount of the Axiom of Choice.
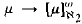. We conclude with a discussion of some consistency questions concerning different versions of the axiom asserting the existence of a nontrivial elementary embedding 