Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T01:55:45.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Jonsson-like partition relations and j: V → V

Published online by Cambridge University Press:  12 March 2014

Arthur W. Apter  and
Grigor Sargsyan
Arthur W. Apter
Affiliation:
Department of Mathematics, Baruch College of CUNY, New York 10010, USA, E-mail: awabb@cunyvm.cuny.edu
Grigor Sargsyan
Affiliation:
Group in Logic and The Methodology of Science, University of CaliforniaBerkeley, California 94720, USA, E-mail: grigor@math.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract.

Working in the theory ”ZF + There is a nontrivial elementary embedding j : V → V“, we show that a final segment of cardinals satisfies certain square bracket finite and infinite exponent partition relations. As a corollary to this, we show that this final segment is composed of Jonsson cardinals. We then show how to force and bring this situation down to small alephs. A prototypical result is the construction of a model for ZF in which every cardinal μ ≥ ℵ2 satisfies the square bracket infinite exponent partition relation 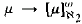. We conclude with a discussion of some consistency questions concerning different versions of the axiom asserting the existence of a nontrivial elementary embedding j: V → V. By virtue of Kunen's celebrated inconsistency result, we use only a restricted amount of the Axiom of Choice.

Keywords

Jonsson cardinalspartition relationspolarized partitionselementary embeddings
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 4 , December 2004 , pp. 1267 - 1281
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Apter, A., Some results on consecutive large cardinals, Annals of Pure and Applied Logic, vol. 25 (1983), pp. 1–17.CrossRefGoogle Scholar
[2]Apter, A., Some results on consecutive large cardinals II: Applications of Radin forcing, Israel Journal of Mathematics, vol. 52 (1985), pp. 273–292.CrossRefGoogle Scholar
[3]Apter, A., Some new upper bounds in consistency strength for certain choiceless large cardinal patterns, Archive for Mathematical Logic, vol. 31 (1992), pp. 201–205.CrossRefGoogle Scholar
[4]Apter, A. and Henle, J. M., Large cardinal structures below ℵω, this Journal, vol. 51 (1986), pp. 591–603.Google Scholar
[5]Apter, A., Henle, J. M., and Jackson, S. C., The calculus of partition sequences, changing cofinalities, and a question of Woodin, Transactions of the American Mathematical Society, vol. 352 (2000), pp. 969–1003.Google Scholar
[6]Corazza, P., The wholeness axiom and Laver sequences, Annals of Pure and Applied Logic, vol. 105 (2000), pp. 157–260.CrossRefGoogle Scholar
[7]Erdős, P. and Hajnal, A., On a problem of B. Jónsson, Bulletin de l' Académie Polonaise des Sciences Série des Sciences Mathématiques Astronomiques, et Physiques, vol. 14 (1966), pp. 19–23.Google Scholar
[8]Galvin, F. and Prikry, K., Infinitary Jonsson algebras and partition relations, Algebra Universalis, vol. 6 (1976), pp. 367–376.CrossRefGoogle Scholar
[9]Gitik, M., All uncountable cardinals can be singular, Israel Journal of Mathematics, vol. 35 (1980), pp. 61–88.CrossRefGoogle Scholar
[10]Gitik, M., Regular cardinals in models of ZF, Transactions of the American Mathematical Society, vol. 290 (1985), pp. 41–68.Google Scholar
[11]Jech, T., The axiom of choice, North-Holland, Amsterdam, London and New York, 1973.Google Scholar
[12]Kanamori, A., The higher infinite, Perspectives in Mathematical Logic, Springer-Verlag, Berlin and New York, 1994.Google Scholar
[13]Kleinberg, E., Infinitary combinatorics and the axiom of determinateness, Lecture Notes in Mathematics, vol. 612, Springer-Verlag, Berlin and New York, 1977.CrossRefGoogle Scholar
[14]Kunen, K., Elementary embeddings and infinitary combinatorics, this Journal, vol. 36 (1971), pp. 407–413.Google Scholar
[15]Kunen, K., Set theory: An introduction to independence proofs, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, Amsterdam, London, and New York, 1980.Google Scholar
[16]Reinhardt, W. N.. Remarks on reflection principles, large cardinals, and elementary embeddings, Axiomatic set theory (Jech, T., editor), vol. 13. Proceedings of Symposia in Pure Mathematics, no. 2, American Mathematical Society, Providence, R. I., 1974, pp. 189–205.Google Scholar
[17]Shioya, S., Infinitary J́nsson functions and elementary embeddings, Archive for Mathematical Logic, vol. 33 (1994), pp. 81–86.CrossRefGoogle Scholar
[18]Suzuki, A., NO elementary embedding from V into V is definable from parameters, this Journal. vol. 64(1999), pp. 1591–1594.Google Scholar
[19]Zapletal, J., A new proof of Kunen's inconsistency, Proceedings of the American Mathematical Society, vol. 124 (1996), pp. 2203–2204.CrossRefGoogle Scholar