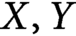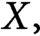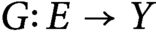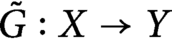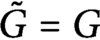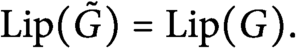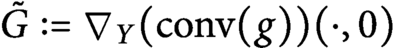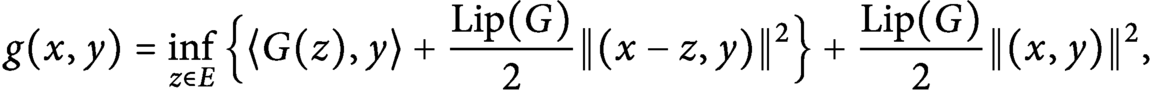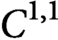1 results
Kirszbraun’s Theorem via an Explicit Formula
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 142-153
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
-
Let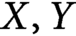
$X,Y$ be two Hilbert spaces, let E be a subset of 
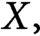$X,$ and let 
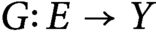$G\colon E \to Y$ be a Lipschitz mapping. A famous theorem of Kirszbraun’s states that there exists 
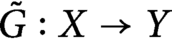$\tilde {G} : X \to Y$ with 
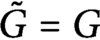$\tilde {G}=G$ on E and 
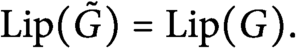$ \operatorname {\mathrm {Lip}}(\tilde {G})= \operatorname {\mathrm {Lip}}(G).$ In this note we show that in fact the function 
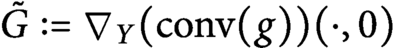$\tilde {G}:=\nabla _Y( \operatorname {\mathrm {conv}} (g))( \cdot , 0)$, where $$\begin{align*}g(x,y) = \inf_{z \in E} \Big\lbrace \langle G(z), y \rangle + \frac{\operatorname{\mathrm{Lip}}(G)}{2} \|(x-z,y)\|^2 \Big\rbrace + \frac{\operatorname{\mathrm{Lip}}(G)}{2}\|(x,y)\|^2, \end{align*}$$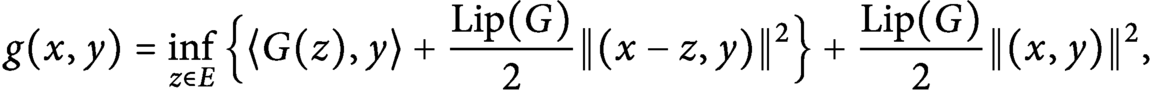defines such an extension. We apply this formula to get an extension result for strongly biLipschitz mappings. Related to the latter, we also consider extensions of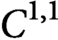
$C^{1,1}$ strongly convex functions.
