3 results
Asymptotic expansions for functionals of dilation of point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 573-591
- Print publication:
- September 1996
-
- Article
- Export citation
On platoon formation on two-lane roads
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 2 / June 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 347-361
- Print publication:
- June 1979
-
- Article
- Export citation
A low traffic approximation for queues
-
- Journal:
- Journal of Applied Probability / Volume 9 / Issue 4 / December 1972
- Published online by Cambridge University Press:
- 14 July 2016, pp. 832-840
- Print publication:
- December 1972
-
- Article
- Export citation

 and
and 
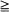 2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.
2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.