Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-29T09:47:06.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic expansions for functionals of dilation of point processes

Part of: Computer system organization Stochastic processes

Published online by Cambridge University Press:  14 July 2016

A. A. Borovkov
A. A. Borovkov*
Affiliation:
Institute of Mathematics, Novosibirsk
*
∗Postal address: Institute of Mathematics, Novosibirsk, 630090, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

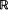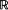This paper provides a direct approach to obtaining formulas for derivatives of functionals of point processes in rare perturbation analysis ([2], [6]). Results are obtained for arbitrary (not necessarily stationary) point processes in and d, d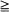 2, under transparent conditions, close to minimal. Formulas for higher-order derivatives allow one to construct asymptotical expansions. The results can be useful in sensitivity analysis, in light traffic theory for queues and for computation by simulation of derivatives at positive intensity, while the computation of the derivatives via statistical estimation of the functional itself and its increments usually gives poor results.

Keywords

SENSITIVITY ANALYSISRARE PERTURBATION ANALYSISLIGHT TRAFFIC

MSC classification

Primary: 60G55: Point processes 68M20: Performance evaluation; queueing; scheduling
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 2 , September 1996 , pp. 573 - 591
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work was supported by grants from Ministère de la Recherche of France, INRIA and INTAS.

References

[1] Baccelli, F. and Bremaud, P. (1987) Palm Probability and Stationary Queueing Systems. (Lecture Notes in Statistics 41). Springer, New York.CrossRefGoogle Scholar
[2] Baccelli, F. and Bremaud, P. (1993) Virtual customers in sensitivity and light traffic analysis via Cambell's formula for point processes. Adv. Appl. Prob. 25, 221–234.CrossRefGoogle Scholar
[3] Baccelli, F., Klein, M. and Zuyev, S. (1994) Perturbation formulas in space. INRIA. Preprint. Google Scholar
[4] Blaszczyszyn, B. (1993) Factorial moment expansion for stochastic systems. University of Wroclaw. Preprint. Google Scholar
[5] Daley, D. J. and Rolski, T. (1994) Light traffic approximation in general stationary single-server queues. Stoch. Proc. Appl. 49, 141–158.CrossRefGoogle Scholar
[6] Reiman, M. I. and Simon, B. (1989) Open queueing systems in light traffic. Math. Operat. Res. 14, 1, 26–59.CrossRefGoogle Scholar