We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Daniels and Skyrme (1985) derived the joint distribution of the maximum, and the time at which it is attained, of a Brownian path superimposed on a parabolic curve near its maximum. In the present paper the results are extended to include Gaussian processes which behave locally like Brownian motion, or a process transformable to it, near the maximum of the mean path. This enables a wider class of practical problems to be dealt with. The results are used to obtain the asymptotic distribution of breaking load and extension of a bundle of fibres which can admit random slack or plastic yield, as suggested by Phoenix and Taylor (1973). Simulations confirm the approximations reasonably well. The method requires consideration not only of a Brownian bridge but also of an analogous process with covariance function t1(1 + t2),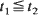 
.
