Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (1)

Articles (1)

Last 3 years (1)

From year:

To year:

Apply

Mathematics (1)

lagrangian representation

Proceedings of the Royal Society of Edinburgh Section A: Mathematics (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

On Lebesgue points of entropy solutions to the eikonal equation
Part of
- General first-order equations and systems
- Partial differential equations
Xavier Lamy, Elio Marconi
Journal:

Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024

Published online by Cambridge University Press:

23 May 2023, pp. 1047-1059

Print publication:

August 2024
- Article
- - You have access
- PDF
- HTML
- Export citation
We consider entropy solutions to the eikonal equation $|\nabla u|=1$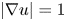 in two-space dimensions. These solutions are motivated by a class of variational problems and fail in general to have bounded variation. Nevertheless, they share several of their fine properties with BV functions: we show in particular that the set of non-Lebesgue points has at least one co-dimension.